3-11 相容关系

 

相容关系与3-11相容关系的深入探讨

相容关系在数学和计算机科学领域中扮演着关键角色，提供了一种分析集合内元素间相互关系的强有力工具。通过本篇博客，我们将详细探讨相容关系及其特定应用—3-11相容关系，以及如何通过关系图和矩阵来直观地理解它们。

相容关系的基本概念

相容关系基于两个主要特性：自反性和对称性。自反性意味着集合A中的每个元素与自己相容，而对称性表明如果元素x与元素y相容，则y与x也相容。这两个条件共同定义了何为相容关系。

相容关系的实例

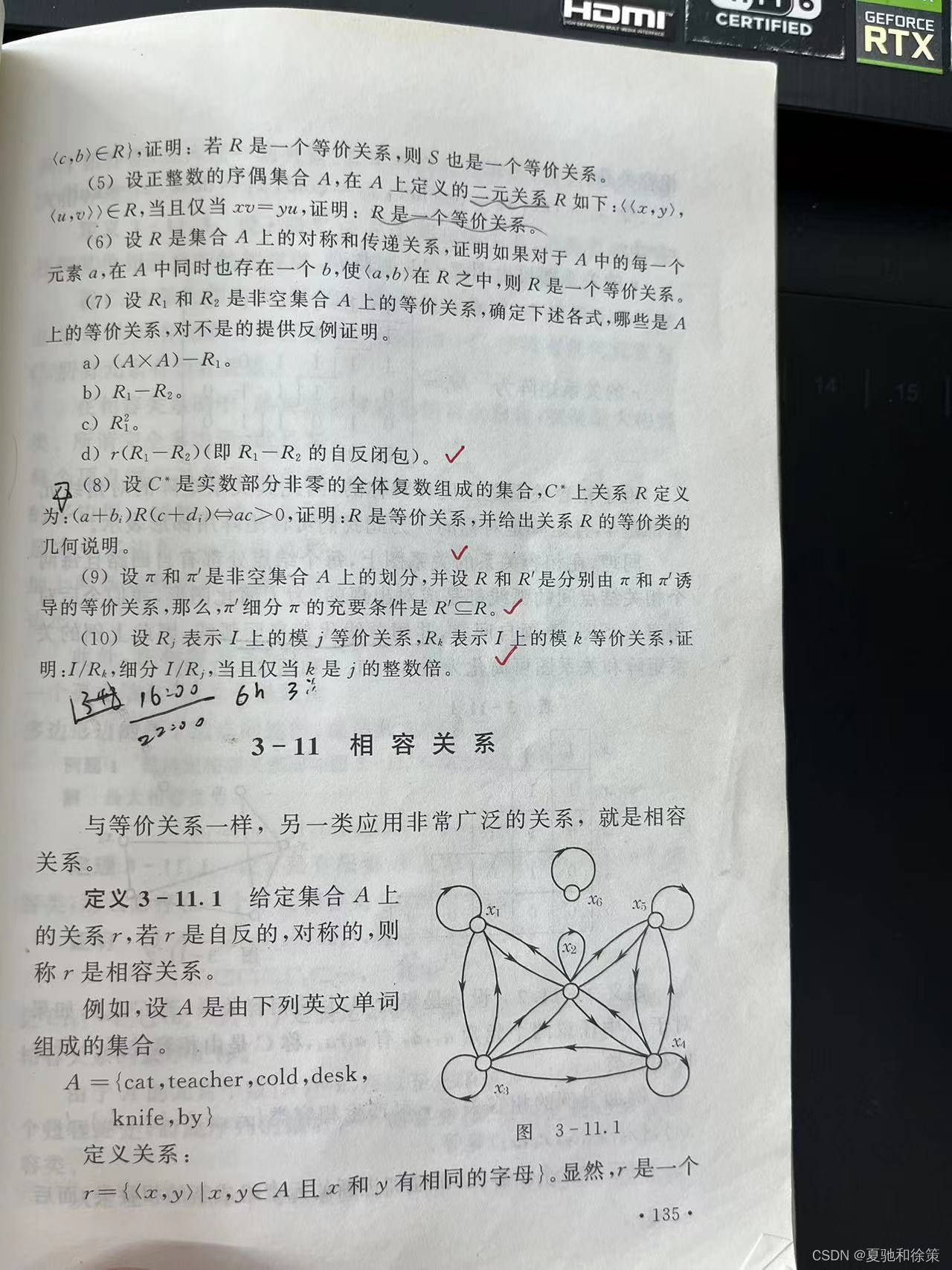
考虑集合A：{cat, teacher, cold, desk, knife, by}。我们定义相容关系r为集合A中任意两个元素x和y有共同字母时它们相容。根据此定义，很显然r构成一个相容关系，因为它既自反又对称。

3-11相容关系的应用

相容类的定义

在相容关系的框架内，相容类是集合A中所有互相相容的元素子集。例如，从集合A出发，我们可以定义多个相容类，例如{cat, cold}和{teacher, desk}等。

最大相容类

一个重要的概念是最大相容类，指的是不能被任何其他相容类包含的相容类。最大相容类表示了在给定相容关系下，集合A中元素相互关联的最大范围。例如，在我们的案例中，集合{cat, cold}可能代表一个最大相容类。

直观理解相容关系

为了更直观地理解相容关系，我们可以借助关系图和关系矩阵。

关系图的描述

在关系图中，节点代表集合中的元素，而边代表元素间的相容关系。由于相容关系的自反和对称特性，每个节点都会有自环，且图形是对称的。

关系矩阵的解析

关系矩阵是一个方阵，行和列代表集合中的元素。如果元素i与元素j相容，则矩阵的(i, j)位置是1，否则为0。这样的矩阵由于相容关系的性质，将是对称的，且对角线上的值为1。

结论

相容关系为理解集合中元素之间的相互作用提供了一种有效的方法。通过分析相容类和最大相容类，我们可以洞察元素间基于共同特征或属性的深层联系。相容关系的图形和矩阵表示法进一步增强了我们对这些关系的直观理解，无论在理论探索还是实际应用中，相容关系都是一个非常有价值的概念。

 

 

在探索相容关系及其在数学和逻辑领域中的应用时，理解如何通过定理和例题来证明关于相容关系的属性是非常重要的。本篇博客旨在深入解析定理3-11.1和定理3-11.2的证明过程，以及它们如何帮助我们理解最大相容类和相容关系的构造。

定理3-11.1的证明解析

定理3-11.1提供了一种方法，证明了对于任何给定的相容类，我们总能找到一个最大相容类，该最大相容类包含了这个给定的相容类。这个证明的关键在于构造一个相容类序列，其中每一步都尝试增加一个新的元素到当前相容类中，直到不能再添加更多元素为止。

证明步骤

1. 初始相容类：从给定的相容类C开始，将其设为序列的第一个元素C₀。
2. 序列构造：对于序列中的每个相容类Cᵢ，尝试找到集合A中的一个元素aⱼ，这个元素不在Cᵢ中，但与Cᵢ中的所有元素都相容。然后，将aⱼ添加到Cᵢ中形成新的相容类Cᵢ₊₁。
3. 终止条件：这个过程将在没有更多元素可以被添加到当前相容类时终止。由于集合A是有限的，这保证了过程最终会停止。

通过这个过程，我们最终得到的相容类将是最大的，因为任何尝试添加新元素都会导致与现有元素不相容，从而验证了定理的正确性。

定理3-11.2的证明概述

定理3-11.2进一步扩展了我们对相容关系的理解，说明了如何从给定集合A的覆盖构造出一个相容关系。这个定理强调了覆盖中的每个子集构造出的关系确实是相容的。

证明要点

1. 自反性：由于覆盖中的每个子集至少包含集合A中的一个元素，因此对于任何元素x，都存在一个子集使得(x, x)属于该子集的笛卡尔积，从而证明了关系的自反性。
2. 对称性：如果(x, y)属于由某个子集构造的关系，则因为这个子集中x和y是相容的，(y, x)也将属于这个关系，证明了对称性。

这两点共同保证了由集合A的任意覆盖构造出的关系是相容的。

最大相容类与完全覆盖

通过定理3-11.1和定理3-11.2的证明，我们了解到集合A上的相容关系如何形成最大相容类，并且如何通过集合覆盖来构造相容关系。这些理论基础帮助我们理解了相容关系的深层结构和性质，特别是在考虑最大相容类和完全覆盖的一一对应关系时。

结论

通过定理的证明，我们不仅能够更深入地理解相容关系的性质，还能够掌握这些关系在数学逻辑和抽象代数中的应用。定理3-11.1和定理3-11.2为我们提供了构造和理解相容关系的强大工具，从而使我们能够探索更复杂的数学结构和理论。