8.12.25 ACM-ICPC数学 数论 Min_25 筛

8.12.25 ACM-ICPC数学 数论 Min_25筛

Min_25筛是一种高效的数论筛法，通常用于计算区间上素数个数、求和函数等。与传统的埃拉托斯特尼筛法相比，Min_25筛在处理大范围数时具有显著优势。本文将详细介绍Min_25筛的原理、实现步骤及应用。

一、Min_25筛的原理

Min_25筛的核心思想是利用数学函数的性质和递归分治思想，将问题分解成多个小问题，从而降低时间复杂度。具体来说，Min_25筛通过预处理小于某个阈值的数，然后利用这些预处理信息快速计算更大范围内的数。

二、Min_25筛的实现步骤

1. 预处理阶段

首先，需要预处理小于某个阈值（如sqrt(n)）的素数及其相关函数值。这可以通过埃拉托斯特尼筛法完成。

const int MAXN = 1000000;
bool is_prime[MAXN];
vector<int> primes;

void eratosthenes_sieve(int n) {
    fill(is_prime, is_prime + n + 1, true);
    is_prime[0] = is_prime[1] = false;
    for (int i = 2; i <= n; ++i) {
        if (is_prime[i]) {
            primes.push_back(i);
            for (int j = i * 2; j <= n; j += i) {
                is_prime[j] = false;
            }
        }
    }
}

2. 分治递归阶段

在预处理完小素数后，使用分治递归的思想处理更大范围内的数。假设我们需要计算区间1,𝑛1,n内的某个数论函数值，可以将区间划分成若干小区间，并利用预处理信息加速计算。

#include <iostream>
#include <vector>
#include <cmath>
#include <unordered_map>

using namespace std;

typedef long long ll;

const int MAXN = 1000000;
vector<int> primes;
bool is_prime[MAXN];
unordered_map<ll, ll> memo;

void sieve(int n) {
    fill(is_prime, is_prime + n + 1, true);
    is_prime[0] = is_prime[1] = false;
    for (int i = 2; i <= n; ++i) {
        if (is_prime[i]) {
            primes.push_back(i);
            for (int j = i * 2; j <= n; j += i) {
                is_prime[j] = false;
            }
        }
    }
}

ll phi(ll x, int a) {
    if (a == 1) return (x + 1) / 2;
    if (memo.count(x)) return memo[x];
    ll res = phi(x, a - 1) - phi(x / primes[a - 1], a - 1);
    memo[x] = res;
    return res;
}

ll pi(ll x) {
    if (x < MAXN) return upper_bound(primes.begin(), primes.end(), x) - primes.begin();
    ll a = pi(sqrt(x)), b = pi(cbrt(x));
    ll sum = phi(x, a) + (a + b - 2) * (a - b + 1) / 2;
    for (ll i = b + 1; i <= a; ++i) {
        ll w = x / primes[i - 1];
        sum -= pi(w);
        if (i <= b) sum += pi(sqrt(w));
    }
    return sum;
}

int main() {
    ll n;
    cin >> n;
    sieve(sqrt(n) + 1);
    cout << pi(n) << endl;
    return 0;
}

三、应用举例

Min_25筛不仅可以用于计算区间上素数的个数，还可以用于求解其他数论函数值。以下是几个常见的应用场景：

1. 计算区间内素数个数

利用Min_25筛，可以快速计算大范围内的素数个数。相比传统方法，时间复杂度大幅降低。

2. 求和函数

例如，求区间内所有数的因子和，Min_25筛通过预处理和递归分治，可以高效地完成计算。

四、总结

Min_25筛是一种强大的数论工具，特别适合处理大范围数论问题。通过预处理小素数和递归分治的方法，Min_25筛能够在较短时间内完成大规模计算。掌握并应用Min_25筛，将大大提升数论问题的求解效率。

希望这篇博客能帮助大家理解和应用Min_25筛。若有疑问或需要进一步交流，欢迎在评论区留言。

---

8.12.25 ACM-ICPC数学 数论 Min_25筛

Min_25筛是一种高效的数论筛法，用于求解积性函数的前缀和问题。与传统的埃拉托斯特尼筛法相比，Min_25筛在处理大范围数时具有显著优势。本文将详细介绍Min_25筛的定义、性质、实现及应用。

定义

Min_25筛，又称为“Extended Eratosthenes Sieve”，由Min_25发明并最早使用，因此得名。

性质

Min_25筛可以在 𝑂(𝑛34log⁡𝑛)O(lognn43​​) 或 Θ(𝑛1−𝜖)Θ(n1−ϵ) 的时间复杂度下解决一类积性函数的前缀和问题。要求 𝑓(𝑝)f(p) 是一个关于 𝑝p 的项数较少的多项式或可以快速求值；𝑓(𝑝𝑐)f(pc) 可以快速求值。

记号

• 

解释

观察 𝐹𝑘(𝑛)Fk​(n) 的定义，可以发现答案即为

考虑如何求出 𝐹𝑘(𝑛)Fk​(n)。通过枚举每个 𝑖i 的最小质因子及其次数可以得到递推式：

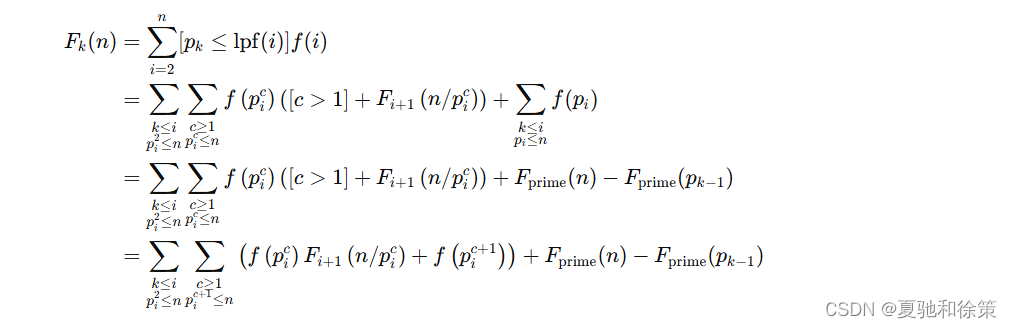
最后一步推导基于这样一个事实：对于满足 𝑝𝑖𝑐≤𝑛<𝑝𝑖𝑐+1pic​≤n<pic+1​ 的 𝑐c，有 𝑝𝑖𝑐+1>𝑛  ⟺  𝑛/𝑝𝑖𝑐<𝑝𝑖<𝑝𝑖+1pic+1​>n⟺n/pic​<pi​<pi+1​，故 𝐹𝑖+1(𝑛/𝑝𝑖𝑐)=0Fi+1​(n/pic​)=0。其边界值即为 𝐹𝑘(𝑛)=0Fk​(n)=0 (𝑝𝑘>𝑛pk​>n)。

假设现在已经求出了所有的 𝐹prime(𝑛)Fprime​(n)，那么有两种方式可以求出所有的 𝐹𝑘(𝑛)Fk​(n)：

1. 直接按照递推式计算。
2. 从大到小枚举 𝑝p 转移，仅当 𝑝2<𝑛p2<n 时转移增加值不为零，故按照递推式后缀和优化即可。

现在考虑如何计算 𝐹prime(𝑛)Fprime​(n)。观察求 𝐹𝑘(𝑛)Fk​(n) 的过程，容易发现 𝐹primeFprime​ 有且仅有 1,2,…,⌊𝑛⌋,𝑛/𝑛,…,𝑛/2,𝑛1,2,…,⌊n​⌋,n/n​,…,n/2,n 这 𝑂(𝑛)O(n​) 处的点值是有用的。

一般情况下，𝑓(𝑝)f(p) 是一个关于 𝑝p 的低次多项式，可以表示为 𝑓(𝑝)=∑𝑎𝑖𝑝𝑐𝑖f(p)=∑ai​pci​。那么对于每个 𝑝𝑐𝑖pci​，其对 𝐹prime(𝑛)Fprime​(n) 的贡献即为 𝑎𝑖∑2≤𝑝≤𝑛𝑝𝑐𝑖ai​∑2≤p≤n​pci​。分开考虑每个 𝑝𝑐𝑖pci​ 的贡献，问题就转变为了：给定 𝑛,𝑠,𝑔(𝑝)=𝑝𝑠n,s,g(p)=ps，对所有的 𝑚=𝑛/𝑖m=n/i，求 ∑𝑝≤𝑚𝑔(𝑝)∑p≤m​g(p)。

Notice：𝑔(𝑝)=𝑝𝑠g(p)=ps 是完全积性函数！

于是设 𝐺𝑘(𝑛):=∑𝑖=1𝑛[𝑝𝑘<lpf⁡(𝑖)∨isprime⁡(𝑖)]𝑔(𝑖)Gk​(n):=∑i=1n​[pk​<lpf(i)∨isprime(i)]g(i)，即埃筛第 𝑘k 轮筛完后剩下的数的 𝑔g 值之和。对于一个合数 𝑥x，必定有 lpf⁡(𝑥)≤𝑥lpf(x)≤x​，则 𝐹prime=𝐺⌊𝑛⌋Fprime​=G⌊n​⌋​，故只需筛到 𝐺⌊𝑛⌋G⌊n​⌋​ 即可。

考虑 𝐺G 的边界值，显然为 𝐺0(𝑛)=∑𝑖=2𝑛𝑔(𝑖)G0​(n)=∑i=2n​g(i)。（还记得吗？特别约定了 𝑝0=1p0​=1）对于转移，考虑埃筛的过程，分开讨论每部分的贡献，有：

1. 

则有：

复杂度分析

对于 𝐹prime(𝑛)Fprime​(n) 的计算，事实上，其实现与洲阁筛第一部分是相同的。考虑对于每个 𝑚=𝑛/𝑖m=n/i，只有在枚举满足 𝑝𝑘2≤𝑚pk2​≤m 的 𝑝𝑘pk​ 转移时会对时间复杂度产生贡献，则时间复杂度可估计为：

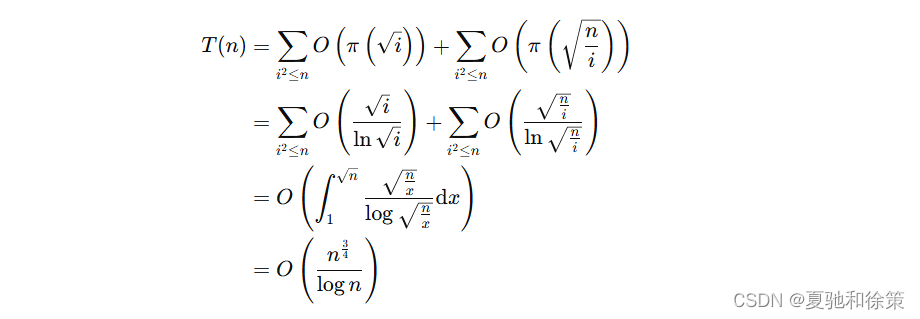
对于空间复杂度，可以发现不论是 𝐹𝑘Fk​ 还是 𝐹primeFprime​，其均只在 𝑛/𝑖n/i 处取有效点值，共 𝑂(𝑛)O(n​) 个，仅记录有效值即可将空间复杂度优化至 𝑂(𝑛)O(n​)。

过程

对于 𝐹𝑘(𝑛)Fk​(n) 的计算，我们实现时一般选择实现难度较低的第一种方法，其在数据规模较小时往往比第二种方法的表现要好；

对于 𝐹prime(𝑛)Fprime​(n) 的计算，直接按递推式实现即可。

用 Extended Eratosthenes Sieve 求 积性函数 𝑓f 的前缀和时，应当明确以下几点：

1. 如何快速（一般是线性时间复杂度）筛出前 𝑛n​ 个 𝑓f 值；
2. 𝑓(𝑝)f(p) 的多项式表示；
3. 如何快速求出 𝑓(𝑝𝑐)f(pc)。

明确上述几点之后按顺序实现以下几部分即可：

1. 筛出 [1, 𝑛n​] 内的质数与前 𝑛n​ 个 𝑓f 值；
2. 对 𝑓(𝑝)f(p) 多项式表示中的每一项筛出对应的 𝐺G，合并得到 𝐹primeFprime​ 的所有 𝑂(𝑛)O(n​) 个有用点值；
3. 按照 𝐹𝑘Fk​ 的递推式实现递归，求出 𝐹1(𝑛)F1​(n)。

例题

求莫比乌斯函数的前缀和

求

易知 直接筛即可得到 𝐹primeFprime​ 的所有 𝑂(𝑛)O(n​) 个所需点值。

求欧拉函数的前缀和

求

∑𝑖=1𝑛𝜑(𝑖)i=1∑n​φ(i)

首先易知 𝑓(𝑝)=𝑝−1f(p)=p−1。对于 𝑓(𝑝)f(p) 的一次项 (p)，有 𝑔(𝑝)=𝑝,𝐺0(𝑛)=∑𝑖=2𝑛𝑔(𝑖)=(𝑛+2)(𝑛−1)2g(p)=p,G0​(n)=∑i=2n​g(i)=2(n+2)(n−1)​；对于 𝑓(𝑝)f(p) 的常数项 (-1)，有 𝑔(𝑝)=−1,𝐺0(𝑛)=∑𝑖=2𝑛𝑔(𝑖)=−𝑛+1g(p)=−1,G0​(n)=∑i=2n​g(i)=−n+1。筛两次加起来即可得到 𝐹primeFprime​ 的所有 𝑂(𝑛)O(n​) 个所需点值。

「LOJ #6053」简单的函数

给定 𝑓(𝑛)f(n)：

易知 𝑓(𝑝)=𝑝−1+2[𝑝=2]f(p)=p−1+2[p=2]。则按照筛 𝜑φ 的方法筛，对 2 讨论一下即可。此处给出一种 C++ 实现：

#include <algorithm>
#include <cmath>
#include <cstdio>

const int maxs = 200000;  // 2sqrt(n)
const int mod = 1000000007;

template <typename x_t, typename y_t>
void inc(x_t &x, const y_t &y) {
  x += y;
  (mod <= x) && (x -= mod);
}

template <typename x_t, typename y_t>
void dec(x_t &x, const y_t &y) {
  x -= y;
  (x < 0) && (x += mod);
}

template <typename x_t, typename y_t>
int sum(const x_t &x, const y_t &y) {
  return x + y < mod ? x + y : (x + y - mod);
}

template <typename x_t, typename y_t>
int sub(const x_t &x, const y_t &y) {
  return x < y ? x - y + mod : (x - y);
}

template <typename _Tp>
int div2(const _Tp &x) {
  return ((x & 1) ? x + mod : x) >> 1;
}

// 以上目的均为防负数和取模
template <typename _Tp>
long long sqrll(const _Tp &x) {  // 平方函数
  return (long long)x * x;
}

int pri[maxs / 7], lpf[maxs + 1], spri[maxs + 1], pcnt;

void sieve(const int &n) {
  for (int i = 2; i <= n; ++i) {
    if (lpf[i] == 0) {  // 记录质数
      lpf[i] = ++pcnt;
      pri[lpf[i]] = i;
      spri[pcnt] = sum(spri[pcnt - 1], i);  // 前缀和
    }
    for (int j = 1, v; j <= lpf[i] && (v = i * pri[j]) <= n; ++j) lpf[v] = j;
  }
}

long long global_n;
int lim;
int le[maxs + 1],  // x <= \sqrt{n}
    ge[maxs + 1];  // x > \sqrt{n}
#define idx(v) (v <= lim ? le[v] : ge[global_n / v])

int G[maxs + 1][2], Fprime[maxs + 1];
long long lis[maxs + 1];
int cnt;

void init(const long long &n) {
  for (long long i = 1, j, v; i <= n; i = n / j + 1) {
    j = n / i;
    v = j % mod;
    lis[++cnt] = j;
    (j <= lim ? le[j] : ge[global_n / j]) = cnt;
    G[cnt][0] = sub(v, 1ll);
    G[cnt][1] = div2((long long)(v + 2ll) * (v - 1ll) % mod);
  }
}

void calcFprime() {
  for (int k = 1; k <= pcnt; ++k) {
    const int p = pri[k];
    const long long sqrp = sqrll(p);
    for (int i = 1; lis[i] >= sqrp; ++i) {
      const long long v = lis[i] / p;
      const int id = idx(v);
      dec(G[i][0], sub(G[id][0], k - 1));
      dec(G[i][1], (long long)p * sub(G[id][1], spri[k - 1]) % mod);
    }
  }
  /* F_prime = G_1 - G_0 */
  for (int i = 1; i <= cnt; ++i) Fprime[i] = sub(G[i][1], G[i][0]);
}

int f_p(const int &p, const int &c) {
  /* f(p^{c}) = p xor c */
  return p xor c;
}

int F(const int &k, const long long &n) {
  if (n < pri[k] || n <= 1) return 0;
  const int id = idx(n);
  long long ans = Fprime[id] - (spri[k - 1] - (k - 1));
  if (k == 1) ans += 2;
  for (int i = k; i <= pcnt && sqrll(pri[i]) <= n; ++i) {
    long long pw = pri[i], pw2 = sqrll(pw);
    for (int c = 1; pw2 <= n; ++c, pw = pw2, pw2 *= pri[i])
      ans +=
          ((long long)f_p(pri[i], c) * F(i + 1, n / pw) + f_p(pri[i], c + 1)) %
          mod;
  }
  return ans % mod;
}

int main() {
  scanf("%lld", &global_n);
  lim = sqrt(global_n);  // 上限

  sieve(lim + 1000);  // 预处理
  init(global_n);
  calcFprime();
  printf("%lld\n", (F(1, global_n) + 1ll + mod) % mod);

  return 0;
}

通过本文的介绍，希望大家能理解Min_25筛的原理和实现方法。Min_25筛是一种非常高效的数论筛法，适用于处理大范围的积性函数问题。如果有疑问或需要进一步交流，欢迎在评论区留言。