uva 679 Dropping Balls

原题：
A number of K balls are dropped one by one from the root of a fully binary tree structure FBT. Each time the ball being dropped first visits a non-terminal node. It then keeps moving down, either follows the path of the left subtree, or follows the path of the right subtree, until it stops at one of the leaf nodes of FBT. To determine a ball’s moving direction a flag is set up in every non-terminal node with two values, either false or true. Initially, all of the flags are false. When visiting a non-terminal node
if the flag’s current value at this node is false, then the ball will first switch this flag’s value, i.e., from the false to the true, and then follow the left subtree of this node to keep moving down. Otherwise, it will also switch this flag’s value, i.e., from the true to the false, but will follow the right subtree of this node to keep moving down. Furthermore, all nodes of FBT are sequentially numbered, starting at 1 with nodes on depth 1, and then those on depth 2, and so on. Nodes on any depth are numbered
from left to right. For example, Fig. 1 represents a fully binary tree of maximum depth 4 with the node numbers 1,2, 3, …, 15. Since all of the flags are initially set to be false, the first ball being dropped will switch flag’s values at node 1, node 2, and node 4 before it finally stops at position 8. The second ball being dropped will switch flag’s values at node 1, node 3, and node 6, and stop at position 12. Obviously, the third ball being dropped will switch flag’s values at node 1, node 2, and node 5 before it stops at
position 10.

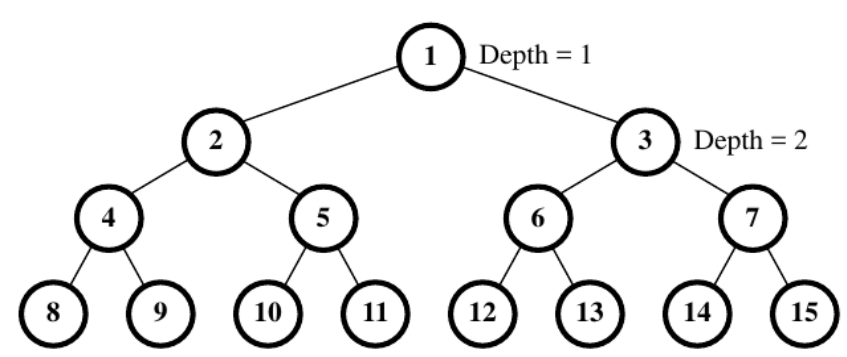
Fig. 1: An example of FBT with the maximum depth 4 and sequential node numbers.
Now consider a number of test cases where two values will be given for each test. The first value is D, the maximum depth of FBT, and the second one is I, the I-th ball being dropped. You may assume the value of I will not exceed the total number of leaf nodes for the given FBT. Please write a program to determine the stop position P for each test case. For each test cases the range of two parameters D and I is as below:
2 ≤ D ≤ 20, and 1 ≤ I ≤ 524288.
Input
Contains l + 2 lines.
Line 1 l the number of test cases
Line 2 D 1 I 1 test case #1, two decimal numbers that are separated by one blank
…
Line k + 1 D k I k test case #k
Line l + 1 D l I l test case #l
Line l + 2 -1 a constant ‘-1’ representing the end of the input file
Output
Contains l lines.
Line 1 the stop position P for the test case #1
…
Line k the stop position P for the test case #k
…
Line l the stop position P for the test case #l
Sample Input
5
4 2
3 4
10 1
2 2
8 128
-1
Sample Output
12
7
512
3
255

中文：
给你一个一个深度为D的完全二叉树，然后给你I个小球，每个二叉树的节点上面有个开关，起始时开关为关闭，小球从根节点下落，如果小球碰到当前开关为关闭状态，那么开关变成打开状态，小球向左，如果当前为打开状态，开关变成关闭，小球向右。问你最后落到的叶子节点的编号是多少？

#include<bits/stdc++.h>
using namespace std;
int main()
{
    ios::sync_with_stdio(false);
    long long D,I;
    int k;
    cin>>k;
    while(k--)
    {
        cin>>D;
        if(D==-1)
            break;
        cin>>I;
        long long ans=1;
        for(long long i=1;i<D;i++)
        {
            if(I%2)
            {
                ans=ans*2;
                I=(I+1)/2;
            }
            else
            {
                ans=ans*2+1;
                I/=2;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

解答：
刘汝佳的经典例题，紫书上有，小白书上也有。可以开个一百万的数组模拟一下，不过也可以发现规律。如果一个节点被走了n次，那么如果n是奇数，当再有小球掉到这个节点上时，就一定是往右子树防线走，如果是偶数一定是往左子树方向走。所以，通过计算小球的编号可以得到它走过的节点是被走过奇数次还是偶数次，判断即可。