前言:本文主要介绍PLSA及EM算法,首先给出LSA(隐性语义分析)的早期方法SVD,然后引入基于概率的PLSA模型,其参数学习采用EM算法。接着我们分析如何运用EM算法估计一个简单的mixture unigram 语言模型和混合高斯模型GMM的参数,最后总结EM算法的一般形式及运用关键点。对于改进PLSA,引入hyperparameter的LDA模型及其Gibbs Sampling参数估计方法放在本系列后面的文章LDA及Gibbs Samping介绍。
1 LSA and SVD
LSA(隐性语义分析)的目的是要从文本中发现隐含的语义维度-即“Topic”或者“Concept”。我们知道,在文档的空间向量模型(VSM)中,文档被表示成由特征词出现概率组成的多维向量,这种方法的好处是可以将query和文档转化成同一空间下的向量计算相似度,可以对不同词项赋予不同的权重,在文本检索、分类、聚类问题中都得到了广泛应用,在基于贝叶斯算法及KNN算法的newsgroup18828文本分类器的JAVA实现和基于Kmeans算法、MBSAS算法及DBSCAN算法的newsgroup18828文本聚类器的JAVA实现系列文章中的分类聚类算法大多都是采用向量空间模型。然而,向量空间模型没有能力处理一词多义和一义多词问题,例如同义词也分别被表示成独立的一维,计算向量的余弦相似度时会低估用户期望的相似度;而某个词项有多个词义时,始终对应同一维度,因此计算的结果会高估用户期望的相似度。
LSA方法的引入就可以减轻类似的问题。基于SVD分解,我们可以构造一个原始向量矩阵的一个低秩逼近矩阵,具体的做法是将词项文档矩阵做SVD分解
其中是以词项(terms)为行, 文档(documents)为列做一个大矩阵. 设一共有t行d列, 矩阵的元素为词项的tf-idf值。然后把
的r个对角元素的前k个保留(最大的k个保留), 后面最小的r-k个奇异值置0, 得到
;最后计算一个近似的分解矩阵
则在最小二乘意义下是
的最佳逼近。由于
最多包含k个非零元素,所以
的秩不超过k。通过在SVD分解近似,我们将原始的向量转化成一个低维隐含语义空间中,起到了特征降维的作用。每个奇异值对应的是每个“语义”维度的权重,将不太重要的权重置为0,只保留最重要的维度信息,去掉一些信息“nosie”,因而可以得到文档的一种更优表示形式。将SVD分解降维应用到文档聚类的JAVA实现可参见此文。
IIR中给出的一个SVD降维的实例如下:
左边是原始矩阵的SVD分解,右边是只保留权重最大2维,将原始矩阵降到2维后的情况。
2 PLSA
尽管基于SVD的LSA取得了一定的成功,但是其缺乏严谨的数理统计基础,而且SVD分解非常耗时。Hofmann在SIGIR'99上提出了基于概率统计的PLSA模型,并且用EM算法学习模型参数。PLSA的概率图模型如下
其中D代表文档,Z代表隐含类别或者主题,W为观察到的单词,表示单词出现在文档
的概率,
表示文档
中出现主题
下的单词的概率,
给定主题
出现单词
的概率。并且每个主题在所有词项上服从Multinomial 分布,每个文档在所有主题上服从Multinomial 分布。整个文档的生成过程是这样的:
而和
分布对应了两组Multinomial 分布,我们需要估计这两组分布的参数。下面给出用EM算法估计PLSA参数的详细推导过程。
3 Estimate parameters in PLSA by EM
(注:本部分主要参考Tomas Hoffman, Unsupervised Learning by Probabilistic Latent Semantic Analysis.)
如文本语言模型的参数估计-最大似然估计、MAP及贝叶斯估计一文所述,常用的参数估计方法有MLE、MAP、贝叶斯估计等等。但是在PLSA中,如果我们试图直接用MLE来估计参数,就会得到似然函数
其中是term
出现在文档
中的次数。注意这是一个关于
和
的函数,一共有N*K + M*K个自变量(注意这里M表示term的总数,一般文献习惯用V表示),如果直接对这些自变量求偏导数,我们会发现由于自变量包含在对数和中,这个方程的求解很困难。因此对于这样的包含“隐含变量”或者“缺失数据”的概率模型参数估计问题,我们采用EM算法。
EM算法的步骤是:
(1)E步骤:求隐含变量Given当前估计的参数条件下的后验概率。
(2)M步骤:最大化Complete data对数似然函数的期望,此时我们使用E步骤里计算的隐含变量的后验概率,得到新的参数值。
两步迭代进行直到收敛。
先解释一下什么是Incomplete data和complete data。Zhai老师在一篇经典的EM算法Notes中讲到,当原始数据的似然函数很复杂时,我们通过增加一些隐含变量来增强我们的数据,得到“complete data”,而“complete data”的似然函数更加简单,方便求极大值。于是,原始的数据就成了“incomplete data”。我们将会看到,我们可以通过最大化“complete data”似然函数的期望来最大化"incomplete data"的似然函数,以便得到求似然函数最大值更为简单的计算途径。
针对我们PLSA参数估计问题,在E步骤中,直接使用贝叶斯公式计算隐含变量在当前参数取值条件下的后验概率,有
在这个步骤中,我们假定所有的和
都是已知的,因为初始时随机赋值,后面迭代的过程中取前一轮M步骤中得到的参数值。
在M步骤中,我们最大化Complete data对数似然函数的期望。在PLSA中,Incomplete data 是观察到的,隐含变量是主题
,那么complete data就是三元组
,其期望是
注意这里是已知的,取的是前面E步骤里面的估计值。下面我们来最大化期望,这又是一个多元函数求极值的问题,可以用拉格朗日乘数法。拉格朗日乘数法可以把条件极值问题转化为无条件极值问题,在PLSA中目标函数就是
,约束条件是:
由此我们可以写出拉格朗日函数
注意这里进行过方程两边同时乘以和
的变形,联立上面4组方程,我们就可以解出M步骤中通过最大化期望估计出的新的参数值
解方程组的关键在于先求出,其实只需要做一个加和运算就可以把
的系数都化成1,后面就好计算了。
然后使用更新后的参数值,我们又进入E步骤,计算隐含变量 Given当前估计的参数条件下的后验概率。如此不断迭代,直到满足终止条件。
注意到我们在M步骤中还是使用对Complete Data的MLE,那么如果我们想加入一些先验知识进入我们的模型,我们可以在M步骤中使用MAP估计。正如文本语言模型的参数估计-最大似然估计、MAP及贝叶斯估计中投硬币的二项分布实验中我们加入“硬币一般是两面均匀的”这个先验一样。而由此计算出的参数的估计值会在分子分母中多出关于先验参数的preduo counts,其他步骤都是一样的。具体可以参考Mei Qiaozhu 的Notes。
PLSA的实现也不难,网上有很多实现code。
例如这个PLSA的EM算法实现 http://ezcodesample.com/plsaidiots/PLSAjava.txt
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
|
class
ProbabilisticLSA
{
private
Dataset dataset =
null
;
private
Posting[][] invertedIndex =
null
;
private
int
M = -
1
;
// number of data
private
int
V = -
1
;
// number of words
private
int
K = -
1
;
// number of topics
public
ProbabilisticLSA()
{
}
public
boolean
doPLSA(String datafileName,
int
ntopics,
int
iters)
{
File datafile =
new
File(datafileName);
if
(datafile.exists())
{
if
((
this
.dataset =
new
Dataset(datafile)) ==
null
)
{
System.out.println(
"doPLSA, dataset == null"
);
return
false
;
}
this
.M =
this
.dataset.size();
this
.V =
this
.dataset.getFeatureNum();
this
.K = ntopics;
//build inverted index
this
.buildInvertedIndex(
this
.dataset);
//run EM algorithm
this
.EM(iters);
return
true
;
}
else
{
System.out.println(
"ProbabilisticLSA(String datafileName), datafile: "
+ datafileName +
" doesn't exist"
);
return
false
;
}
}
//Build the inverted index for M-step fast calculation. Format:
//invertedIndex[w][]: a unsorted list of document and position which word w
// occurs.
//@param ds the dataset which to be analysis
@SuppressWarnings
(
"unchecked"
)
private
boolean
buildInvertedIndex(Dataset ds)
{
ArrayList<Posting>[] list =
new
ArrayList[
this
.V];
for
(
int
k=
0
; k<
this
.V; ++k) {
list[k] =
new
ArrayList<Posting>();
}
for
(
int
m =
0
; m <
this
.M; m++)
{
Data d = ds.getDataAt(m);
for
(
int
position =
0
; position < d.size(); position++)
{
int
w = d.getFeatureAt(position).dim;
// add posting
list[w].add(
new
Posting(m, position));
}
}
// convert to array
this
.invertedIndex =
new
Posting[
this
.V][];
for
(
int
w =
0
; w <
this
.V; w++)
{
this
.invertedIndex[w] = list[w].toArray(
new
Posting[
0
]);
}
return
true
;
}
private
boolean
EM(
int
iters)
{
// p(z), size: K
double
[] Pz =
new
double
[
this
.K];
// p(d|z), size: K x M
double
[][] Pd_z =
new
double
[
this
.K][
this
.M];
// p(w|z), size: K x V
double
[][] Pw_z =
new
double
[
this
.K][
this
.V];
// p(z|d,w), size: K x M x doc.size()
double
[][][] Pz_dw =
new
double
[
this
.K][
this
.M][];
// L: log-likelihood value
double
L = -
1
;
// run EM algorithm
this
.init(Pz, Pd_z, Pw_z, Pz_dw);
for
(
int
it =
0
; it < iters; it++)
{
// E-step
if
(!
this
.Estep(Pz, Pd_z, Pw_z, Pz_dw))
{
System.out.println(
"EM, in E-step"
);
}
// M-step
if
(!
this
.Mstep(Pz_dw, Pw_z, Pd_z, Pz))
{
System.out.println(
"EM, in M-step"
);
}
L = calcLoglikelihood(Pz, Pd_z, Pw_z);
System.out.println(
"["
+ it +
"]"
+
"\tlikelihood: "
+ L);
}
//print result
for
(
int
m =
0
; m <
this
.M; m++)
{
double
norm =
0.0
;
for
(
int
z =
0
; z <
this
.K; z++) {
norm += Pd_z[z][m];
}
if
(norm <=
0.0
) norm =
1.0
;
for
(
int
z =
0
; z <
this
.K; z++) {
System.out.format(
"%10.4f"
, Pd_z[z][m]/norm);
}
System.out.println();
}
return
false
;
}
private
boolean
init(
double
[] Pz,
double
[][] Pd_z,
double
[][] Pw_z,
double
[][][] Pz_dw)
{
// p(z), size: K
double
zvalue = (
double
)
1
/ (
double
)
this
.K;
for
(
int
z =
0
; z <
this
.K; z++)
{
Pz[z] = zvalue;
}
// p(d|z), size: K x M
for
(
int
z =
0
; z <
this
.K; z++)
{
double
norm =
0.0
;
for
(
int
m =
0
; m <
this
.M; m++)
{
Pd_z[z][m] = Math.random();
norm += Pd_z[z][m];
}
for
(
int
m =
0
; m <
this
.M; m++)
{
Pd_z[z][m] /= norm;
}
}
// p(w|z), size: K x V
for
(
int
z =
0
; z <
this
.K; z++)
{
double
norm =
0.0
;
for
(
int
w =
0
; w <
this
.V; w++)
{
Pw_z[z][w] = Math.random();
norm += Pw_z[z][w];
}
for
(
int
w =
0
; w <
this
.V; w++)
{
Pw_z[z][w] /= norm;
}
}
// p(z|d,w), size: K x M x doc.size()
for
(
int
z =
0
; z <
this
.K; z++)
{
for
(
int
m =
0
; m <
this
.M; m++)
{
Pz_dw[z][m] =
new
double
[
this
.dataset.getDataAt(m).size()];
}
}
return
false
;
}
private
boolean
Estep(
double
[] Pz,
double
[][] Pd_z,
double
[][] Pw_z,
double
[][][] Pz_dw)
{
for
(
int
m =
0
; m <
this
.M; m++)
{
Data data =
this
.dataset.getDataAt(m);
for
(
int
position =
0
; position < data.size(); position++)
{
// get word(dimension) at current position of document m
int
w = data.getFeatureAt(position).dim;
double
norm =
0.0
;
for
(
int
z =
0
; z <
this
.K; z++)
{
double
val = Pz[z] * Pd_z[z][m] * Pw_z[z][w];
Pz_dw[z][m][position] = val;
norm += val;
}
// normalization
for
(
int
z =
0
; z <
this
.K; z++)
{
Pz_dw[z][m][position] /= norm;
}
}
}
return
true
;
}
private
boolean
Mstep(
double
[][][] Pz_dw,
double
[][] Pw_z,
double
[][] Pd_z,
double
[] Pz)
{
// p(w|z)
for
(
int
z =
0
; z <
this
.K; z++)
{
double
norm =
0.0
;
for
(
int
w =
0
; w <
this
.V; w++)
{
double
sum =
0.0
;
Posting[] postings =
this
.invertedIndex[w];
for
(Posting posting : postings)
{
int
m = posting.docID;
int
position = posting.pos;
double
n =
this
.dataset.getDataAt(m).getFeatureAt(position).weight;
sum += n * Pz_dw[z][m][position];
}
Pw_z[z][w] = sum;
norm += sum;
}
// normalization
for
(
int
w =
0
; w <
this
.V; w++)
{
Pw_z[z][w] /= norm;
}
}
// p(d|z)
for
(
int
z =
0
; z <
this
.K; z++)
{
double
norm =
0.0
;
for
(
int
m =
0
; m <
this
.M; m++)
{
double
sum =
0.0
;
Data d =
this
.dataset.getDataAt(m);
for
(
int
position =
0
; position < d.size(); position++)
{
double
n = d.getFeatureAt(position).weight;
sum += n * Pz_dw[z][m][position];
}
Pd_z[z][m] = sum;
norm += sum;
}
// normalization
for
(
int
m =
0
; m <
this
.M; m++)
{
Pd_z[z][m] /= norm;
}
}
//This is definitely a bug
//p(z) values are even, but they should not be even
double
norm =
0.0
;
for
(
int
z =
0
; z <
this
.K; z++)
{
double
sum =
0.0
;
for
(
int
m =
0
; m <
this
.M; m++)
{
sum += Pd_z[z][m];
}
Pz[z] = sum;
norm += sum;
}
// normalization
for
(
int
z =
0
; z <
this
.K; z++)
{
Pz[z] /= norm;
//System.out.format("%10.4f", Pz[z]); //here you can print to see
}
//System.out.println();
return
true
;
}
private
double
calcLoglikelihood(
double
[] Pz,
double
[][] Pd_z,
double
[][] Pw_z)
{
double
L =
0.0
;
for
(
int
m =
0
; m <
this
.M; m++)
{
Data d =
this
.dataset.getDataAt(m);
for
(
int
position =
0
; position < d.size(); position++)
{
Feature f = d.getFeatureAt(position);
int
w = f.dim;
double
n = f.weight;
double
sum =
0.0
;
for
(
int
z =
0
; z <
this
.K; z++)
{
sum += Pz[z] * Pd_z[z][m] * Pw_z[z][w];
}
L += n * Math.log10(sum);
}
}
return
L;
}
}
public
class
PLSA {
public
static
void
main(String[] args) {
ProbabilisticLSA plsa =
new
ProbabilisticLSA();
//the file is not used, the hard coded data is used instead, but file name should be valid,
//just replace the name by something valid.
plsa.doPLSA(
"C:\\Users\\APolar\\workspace\\PLSA\\src\\data.txt"
,
2
,
60
);
System.out.println(
"end PLSA"
);
}
}
|
4. Estimate parameters in a simple mixture unigram language model by EM
在PLSA的参数估计中,我们使用了EM算法。EM算法经常用来估计包含“缺失数据”或者“隐含变量”模型的参数估计问题。这两个概念是互相联系的,当我们的模型中有“隐含变量”时,我们会认为原始数据是“不完全的数据”,因为隐含变量的值无法观察到;反过来,当我们的数据incomplete时,我们可以通过增加隐含变量来对“缺失数据”建模。
为了加深对EM算法的理解,下面我们来看如何用EM算法来估计一个简单混合unigram语言模型的参数。本部分主要参考Zhai老师的EM算法Notes。
4.1 最大似然估计与隐含变量引入
所谓unigram语言模型,就是构建语言模型是抛弃所有上下文信息,认为一个词出现的概率与其所在位置无关,具体概率图模型可以参见LDA及Gibbs Samping一文中的介绍。什么是混合模型(mixture model)呢?通俗的说混合概率模型就是由最基本的概率分布比如正态分布、多元分布等经过线性组合形成的新的概率模型,比如混合高斯模型就是由K个高斯分布线性组合而得到。混合模型中产生数据的确切“component model”对我们是隐藏的。我们假设混合模型包含两个multinomial component model,一个是背景词生成模型,另一个是主题词生成模型
。注意这种模型组成方式在概率语言模型中很常见。为了表示单词是哪个模型生成的,我们会为每个单词增加一个布尔类型的控制变量。
文档的对数似然函数为
为第i个文档中的第j个词,
为表示文档中背景词比例的参数,通常根据经验给定。因此
是已知的,我们只需要估计
即可。
同样的我们首先试图用最大似然估计来估计参数。也就是去找最大化似然函数的参数值,有
这是一个关于的函数,同样的,
包含在了对数和中。因此很难求解极大值,用拉格朗日乘数法,你会发现偏导数等于0得到的方程很难求解。所以我们需要依赖数值算法,而EM算法就是其中常用的一种。
我们为每个单词引入一个布尔类型的变量z表示该单词是background word 还是topic word.即
这里我们假设"complete data"不仅包含可以观察到F中的所有单词,而且还包括隐含的变量z。那么根据EM算法,在E步骤我们计算“complete data”的对数似然函数有
比较一下和
,求和运算在对数之外进行,因为此时通过控制变量z的设置,我们明确知道了单词是由背景词分布还是topic 词分布产生的。
和
的关系是怎样的呢?如果带估计参数是
,原始数据是X,对于每一个原始数据分配了一个隐含变量H,则有
4.2 似然函数的下界分析
EM算法的基本思想就是初始随机给定待估计参数的值,然后通过E步骤和M步骤两步迭代去不断搜索更好的参数值。更好的参数值应该要满足使得似然函数更大。我们假设一个潜在的更好参数值是,第n次迭代M步骤得到的参数估计值是
,那么两个参数值对应的似然函数和"complete data"的似然函数的差满足
我们寻找更好参数值的目标就是要最大化,也等价于最大化
。我们来计算隐含变量在给定当前数据X和当前估计的参数值
条件下的条件概率分布即
,有
于是我们得到了潜在更好参数值的incomplete data似然函数的下界。这里我们尤其要注意右边后两项为常数,因为不包含
。所以incomplete data似然函数的下界就是complete data似然函数的期望,也就是诸多EM算法讲义中出现的Q函数,表达式为
可以看出这个期望等于complete data似然函数乘以对应隐含变量条件概率再求和。对于我们要求解的问题,Q函数就是
这里多解释几句Q函数。单词相应的变量z为0时,单词为topic word,从多元分布中产生;当z为1时,单词为background word,从多元分布
产生。同时我们也可以看到如何求Q函数即complete data似然函数的期望,也就是我们要最大化的那个期望(EM算法最大化期望指的就是这个期望),我们要特别关注隐含变量在观察到数据X和前一轮估计出的参数值
条件下取不同值的概率,而隐含变量不同的值对应complete data的不同的似然函数,我们要计算的所谓的期望就是指complete data的似然函数值在不同隐含变量取值情况下的期望值。
4.3 EM算法的一般步骤
通过4.2部分的分析,我们知道,如果我们在下一轮迭代中可以找到一个更好的参数值使得
(1) 随机初始化参数值,也可以根据任何关于最佳参数取值范围的先验知识来初始化
。
(a) E步骤(求期望) 计算Q函数
这里需要注意如何尽量保证EM算法可以找到全局最优解而不是局部最优解呢?第一种方法是尝试许多不同的参数初始值,然后从得到的很多估计出的参数值中选取最优的;第二种方法是通过一个更简单的模型比如只有唯一全局最大值的模型来决定复杂模型的初始值。
通过前面的分析可以知道,EM算法的优势在于complete data的似然函数更容易最大化,因为已经假定了隐含变量的取值,当然要乘以隐含变量取该值的条件概率,所以最终变成了最大化期望值。由于隐含变量变成了已知量,Q函数比原始incomplete data的似然函数更容易求最大值。因此对于“缺失数据”的情况,我们通过引入隐含变量使得complete data的似然函数容易最大化。
在E步骤中,主要的计算难点在于计算隐含变量的条件概率,在PLSA中就是
在我们这个简单混合语言模型的例子中就是
我们假设z的取值只于当前那一个单词有关,计算很容易,但是在LDA中用这种方法计算隐含变量的条件概率和最大化Q函数就比较复杂,可以参见原始LDA论文的参数推导部分。我们也可以用更简单的Gibbs Sampling来估计参数,具体可以参见LDA及Gibbs Samping。
继续我们的问题,下面便是M步骤。使用拉格朗日乘数法来求Q函数的最大值,约束条件是
构造拉格朗日辅助函数
令偏导数为0解出来唯一的极值点
容易知道这里唯一的极值点就是最值点了。注意这里Zhai老师变换了一下变量表示,把对文档里面词的遍历转化成了对词典里面的term的遍历,因为z的取值至于对应的那一个单词有关,与上下文无关。因此E步骤求隐含变量的条件概率公式也相应变成了
最后我们就得到了简单混合Unigram语言模型的EM算法更新公式
即E步骤 求隐含变量条件概率和M步骤 最大化期望估计参数的公式
整个计算过程我们可以看到,我们不需要明确求出Q函数的表达式。取而代之的是我们计算隐含变量的条件概率,然后通过最大化Q函数来得到新的参数估计值。
因此EM算法两步迭代的过程实质是在寻找更好的待估计参数的值使得原始数据即incomplete data似然函数的下界不断提升,而这个“下界“就是引入隐含变量之后的complete data似然函数的期望,也就是诸多EM算法讲义中出现的Q函数,通过最大化Q函数来寻找更优的参数值。同时,上一轮估计出的参数值会在下一轮E步骤中当成已知条件计算隐含变量的条件概率,而这个条件概率又是最大化Q函数求新的参数值是所必需的。
5. Estimate parameters in GMM by EM
经过第3部分和第4部分用EM算法求解PLSA和简单unigram混合模型参数估计问题的详细分析,相信大部分读者已经对EM算法有了一定理解。关于EM算法的材料包括PRML会首先介绍用EM算法去求解混合高斯模型GMM的参数估计问题。下面就让我们来看看如何用EM算法来求解混合高斯模型GMM。
混合高斯模型GMM由K个高斯模型的线性组合组成,高斯模型就是正态分布模型,其中每个高斯模型我们成为一个”Component“,GMM的概率密度函数就是这K个高斯模型概率密度函数的线性组合即
其中
就是高斯分布即正态分布的概率密度函数。这是x为向量的情况,对于x为标量的情况就是
大部分读者应该对标量情形的概率分布更熟悉。这里啰嗦几句,最近看机器学习的论文和书籍,里面的随机变量基本都是多维向量,向量的计算比如加减乘除和求导运算都和标量运算有一些区别,尤其是求导运算,向量和矩阵的求导运算会麻烦很多,看pluskid推荐的一本册子Matrix Cookbook,里面有很多矩阵求导公式,直接查阅应该会更方便。
下面继续说GMM。根据上面给出的概率密度函数,如果我们要从 GMM 的分布中Sample一个样本,实际上可以分为两步:首先随机地在这  个 Component 之中选一个,每个 Component 被选中的概率实际上就是它的系数
个 Component 之中选一个,每个 Component 被选中的概率实际上就是它的系数  ,选中了 Component 之后,再单独地考虑从这个 Component 的分布中选取一个样本点就可以了。在PRML上,引入了一个K维二值随机变量z,只有1维是1,其他维都是0。唯一那个非零的维对应的就是GMM参数样本时被选中的那个高斯分布,而某一维非零的概率就是
,选中了 Component 之后,再单独地考虑从这个 Component 的分布中选取一个样本点就可以了。在PRML上,引入了一个K维二值随机变量z,只有1维是1,其他维都是0。唯一那个非零的维对应的就是GMM参数样本时被选中的那个高斯分布,而某一维非零的概率就是 ,即
,即
下面我们开始估计GMM的参数,包括这K个高斯分布的所有均值和方差以及线性组合的系数。我们给每个样本数据增加一个隐含变量, 就是上面所说的K维向量,表明了
是从哪个高斯分布中sample出来的。对应的概率图模型就是
观察变量的对数似然函数为
注意这里我们定义了表示后验概率
,也就是第n个样本是有第k个高斯分布产生的概率。可以解出
就是由第K个高斯分布产生的样本点的总数;用聚类的观点看,就是聚到cluster k的样本点总数。然后我们将对数似然函数对
求偏导数,令偏导数为0,得到协方差矩阵
最后我们求系数 。注意到系数的和为1,即
。注意到系数的和为1,即
这就是约束条件,最大化对数似然函数又成为了条件极值问题。我们仍然用拉格朗日乘数法,构造辅助函数如下
这样我们就估计出来系数项。
因此用EM算法估计GMM参数的步骤如下
(1) E步骤:估计数据由每个 Component 生成的概率:对于每个数据 来说,它由第
 个 Component 生成的概率为
个 Component 生成的概率为
注意里面  和
和  也是需要我们估计的值,在E步骤我们假定
也是需要我们估计的值,在E步骤我们假定  和
和  均已知,我们使用上一次迭代所得的值(或者初始值)。
均已知,我们使用上一次迭代所得的值(或者初始值)。
(2)M步骤:由最大估计求出高斯分布的所有均值、方差和线性组合的系数,更新待估计的参数值,根据上面的推导,计算公式是
其中
(3)重复迭代E步骤和M步骤,直到似然函数
收敛时算法停止。
更多关于EM算法的深入分析,可以参考PRML第9章内容。
最后我们给出用EM算法估计GMM参数的Matlab实现,出自pluskid的博客:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
|
function varargout = gmm(X, K_or_centroids)
% ============================================================
% Expectation-Maximization iteration implementation of
% Gaussian Mixture Model.
%
% PX = GMM(X, K_OR_CENTROIDS)
% [PX MODEL] = GMM(X, K_OR_CENTROIDS)
%
% - X: N-by-D data matrix.
% - K_OR_CENTROIDS: either K indicating the number of
% components or a K-by-D matrix indicating the
% choosing of the initial K centroids.
%
% - PX: N-by-K matrix indicating the probability of each
% component generating each point.
% - MODEL: a structure containing the parameters
for
a GMM:
% MODEL.Miu: a K-by-D matrix.
% MODEL.Sigma: a D-by-D-by-K matrix.
% MODEL.Pi: a
1
-by-K vector.
% ============================================================
threshold = 1e-
15
;
[N, D] = size(X);
if
isscalar(K_or_centroids)
K = K_or_centroids;
% randomly pick centroids
rndp = randperm(N);
centroids = X(rndp(
1
:K), :);
else
K = size(K_or_centroids,
1
);
centroids = K_or_centroids;
end
% initial values
[pMiu pPi pSigma] = init_params();
Lprev = -inf;
while
true
Px = calc_prob();
%
new
value
for
pGamma
pGamma = Px .* repmat(pPi, N,
1
);
pGamma = pGamma ./ repmat(sum(pGamma,
2
),
1
, K);
%
new
value
for
parameters of each Component
Nk = sum(pGamma,
1
);
pMiu = diag(
1
./Nk) * pGamma' * X;
pPi = Nk/N;
for
kk =
1
:K
Xshift = X-repmat(pMiu(kk, :), N,
1
);
pSigma(:, :, kk) = (Xshift' * ...
(diag(pGamma(:, kk)) * Xshift)) / Nk(kk);
end
% check
for
convergence
L = sum(log(Px*pPi'));
if
L-Lprev < threshold
break
;
end
Lprev = L;
end
if
nargout ==
1
varargout = {Px};
else
model = [];
model.Miu = pMiu;
model.Sigma = pSigma;
model.Pi = pPi;
varargout = {Px, model};
end
function [pMiu pPi pSigma] = init_params()
pMiu = centroids;
pPi = zeros(
1
, K);
pSigma = zeros(D, D, K);
% hard assign x to each centroids
distmat = repmat(sum(X.*X,
2
),
1
, K) + ...
repmat(sum(pMiu.*pMiu,
2
)', N,
1
) - ...
2
*X*pMiu';
[dummy labels] = min(distmat, [],
2
);
for
k=
1
:K
Xk = X(labels == k, :);
pPi(k) = size(Xk,
1
)/N;
pSigma(:, :, k) = cov(Xk);
end
end
function Px = calc_prob()
Px = zeros(N, K);
for
k =
1
:K
Xshift = X-repmat(pMiu(k, :), N,
1
);
inv_pSigma = inv(pSigma(:, :, k));
tmp = sum((Xshift*inv_pSigma) .* Xshift,
2
);
coef = (
2
*pi)^(-D/
2
) * sqrt(det(inv_pSigma));
Px(:, k) = coef * exp(-
0.5
*tmp);
end
end
end
|
6 全文总结
本文主要介绍PLSA及EM算法,首先给出LSA(隐性语义分析)的早期方法SVD,然后引入基于概率的PLSA模型,接着我们详细分析了如何用EM算法估计PLSA、混合unigram 语言模型及混合高斯模型的参数过程,并总结了EM算法的一般形式和运用关键点。关于EM算法收敛性的证明可以参考斯坦福机器学习课程CS229 Andrew Ng老师的课程notes和JerryLead的笔记。EM算法在”缺失数据“和包含”隐含变量“的概率模型参数估计问题中非常常用,是机器学习、数据挖掘及NLP研究必须掌握的算法。
参考文献及推荐Notes
本文主要参考了Hoffman的PLSA论文、Zhai老师的EM Notes以及PRML第9章内容。
[1] Christopher M. Bishop. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag New York, Inc., Secaucus, NJ, USA, 2006.
[2] Gregor Heinrich. Parameter estimation for text analysis. Technical report, 2004.
[3] Wayne Xin Zhao, Note for pLSA and LDA, Technical report, 2011.
[4] Freddy Chong Tat Chua. Dimensionality reduction and clustering of text documents.Technical report, 2009.
[5] CX Zhai, A note on the expectation-maximization (em) algorithm 2007
[6] Qiaozhu Mei, A Note on EM Algorithm for Probabilistic Latent Semantic Analysis 2008
[7] pluskid, 漫谈Clustering, Gaussina Mixture Model
[8] Christopher D. Manning, Prabhakar Raghavan and Hinrich Schütze, Introduction to Information Retrieval, Cambridge University Press. 2008.
[9] Tomas Hoffman, Unsupervised Learning by Probabilistic Latent Semantic Analysis. 2011












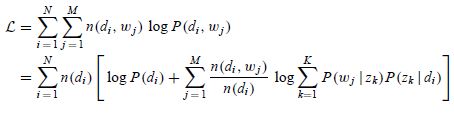




























































 7万+
7万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








