平面曲线参数拟合

对于平面曲线，参数方法一般可以表示为：

在拟合时，需要选择一些基函数$B_{i}(t)$，使得：

比如使用幂基函数：

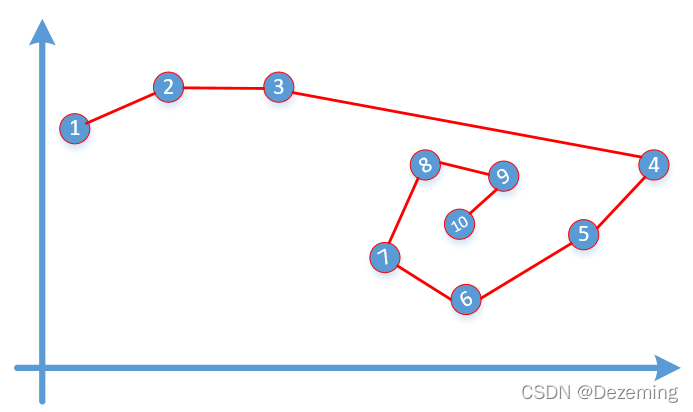
假如现在平面上已经有了一些点集（序号是顺序）：

 

最简单和直白的方式是连起来，如上图右。但是这样不够平滑，我们一般会进行拟合。

拟合方法一般使用最小二乘法，可以将$x(t)$和$y(t)$分别进行拟合。对于$i\in [1,2,...,n]$:

我们需要确定 $t$ 的取值位置。比如令 $t_{i}$ 均匀地分布在$[0,1]$之间（分布在任意的$[a,b]$之间都可以）:

但是这样往往不够细致，比如如果有两个点$p_{3}$和$p_{4}$距离比较远，那么$t_{3}$和$t_{4}$也应该要比较远：

 

因此可以根据两点距离除以总距离来生成不均匀的$t_{i}$:

\section{拟合方法}

当我们使用基函数时，可以写为一个矩阵形式：

令$m=n-1$，$\mathbf{A}$是一个$n\times n$的矩阵，可以直接求解线性系统，但是此时有可能$\mathbf{A}$是一个很接近奇异矩阵的矩阵，因此求逆会有很大的误差。

当$n<m$时，可以应用最小二乘法。我们计算拟合的误差函数：

对误差函数进行求导，令导数为$0$，得到：