稀疏表示学习

1.提出问题：什么是稀疏表示
假设我们用一个M*N的矩阵表示数据集X，每一行代表一个样本，每一列代表样本的一个属性，一般而言，该矩阵是稠密的，即大多数元素不为0。
稀疏表示的含义是，寻找一个系数矩阵A（K*N）以及一个字典矩阵B（M*K），使得B*A尽可能的还原X，且A尽可能的稀疏。A便是X的稀疏表示。
书上原文为（将一个大矩阵变成两个小矩阵，而达到压缩）

“为普通稠密表达的样本找到合适的字典，将样本转化为合适的稀疏表达形式，从而使学习任务得以简化，模型复杂度得以降低，通常称为‘字典学习’（dictionary learning），亦称‘稀疏编码’（sparse coding）”块内容

表达为优化问题的话，字典学习的最简单形式为：

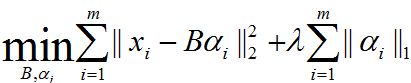
其中xi为第i个样本，B为字典矩阵，aphai为xi的稀疏表示，lambda为大于0参数。
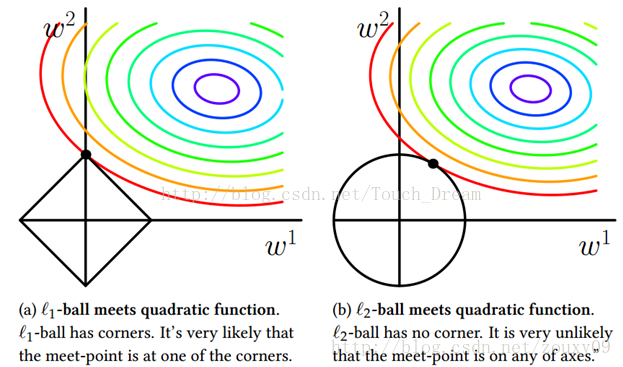
上式中第一个累加项说明了字典学习的第一个目标是字典矩阵与稀疏表示的线性组合尽可能的还原样本；第二个累加项说明了alphai应该尽可能的稀疏。之所以用L1范式是因为L1范式正则化更容易获得稀疏解。具体原因参看该书11.4章或移步机器学习中的范数规则化之（一）L0、L1与L2范数。字典学习便是学习出满足上述最优化问题的字典B以及样本的稀疏表示A（A{alpha1，alpha2，…，alphai}）。L1正则化常用于稀疏，可以获得稀疏解。如下图表示，L1正则化交点在轴上，所得的解一般只是在某个轴上有实数，另外的轴为0，从而最终得到稀疏解。

2.字典学习求解 （学习字典、稀疏表示）
求解上述最优化问题的总体策略是，对字典B以及样本稀疏表示alphai交替迭代优化。即先初始化字典B，

1.固定字典B对alphai进行优化。2.固定A对字典B进行优化。重复上述两步，求得最终B以及X的稀疏表示A。
其中第一步可采用与LASSO正则化相似的方法（如Proximal Gradient Desent法）进行求解，第二步可采用KSVD方法进行求解。具体步骤参看该书11.5章节内容

参考：

http://blog.csdn.net/sam92/article/details/50731607

http://blog.csdn.net/zouxy09/article/details/24971995/