恰好翻到了以前记的cs229的笔记, 其实也想了好久要不要跟风去推导公式, 写写就当是复习一下了
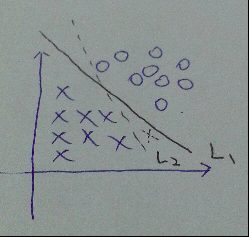
说到svm, 按套路就要先说说线性分类器, 如图, 在特征维数为2时, 可以用一条线将正负样本分离开来.当然了, 这条线可以有无数条, 假设我们训练得到了L2, 而L1是真正的那条直线, 对于新的测试样本(虚线的x), 显然, 用L2分类就会出现误分类. 也就是说, 线性分类器的效果并不怎么好, 但是很多都会把它作为概念的引入课程
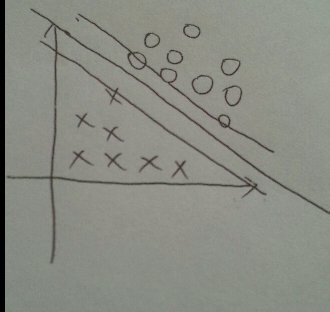
后来92年有人提出了用一对平行的边界(boundry)来将正负样本(Pos/Neg example)分开, 其中中线确定了超平面(hyperplane)的位置, 如图.
两个边界的距离, 我们称之为margin. 我们的目的是, 让这个margin尽可能的大, 最大边界上的正负样本, 我们称它们为支持向量(support vector). 所以如图, 对于垂直于超平面的单位向量w, 以及某个正样本的支持向量u, u在w上的投影便是右上的超平面到原点的距离, 即 wᐧu
可见正样本都是分布在wᐧu>= c 的区域(大于某个距离的区域), c是某个定常数. 令c = -b, 公式改写成
wᐧu+ b >= 0 (decision rule)
所以对任意的正样本x, 我们令
wᐧx + b >= 1
同理, 对于负样本x
wᐧx + b <= - 1
相应的, 对于正负样本的标签, 分别是 y = 1 与 y=-1
这样不论对于正样本还是负样本, 我们都有
y(wᐧx + b) >= 1
变形
y(wᐧx + b) - 1>= 0
对于在边界上的正负样本, 有
y(wᐧx + b) - 1 = 0
如图, 对于正负两个支持向量, 作差可以得到连接两个边界的一个向量, 再点乘前面的单位向量w, 得到了该向量在w方向上的投影, 便得到了margin的大小
到这里, 想想为什么要||w||的最小二乘方?而不是一次, 四次方? ( cs229 Andrew的提问)
最小二乘法在很多假设下都有意义(make sense) (Andrew的回答)
问题转化为如图形式, 这是一个凸二次规划问题(convex quadratic programming), 具体什么是凸二次规划问题, 可以参考<<统计学习方法>> 100页, 该页还有最大间隔存在的唯一性的证明
在这个形式下, 就是在y(wx+b)>=1的条件下最小化 ||w||的平方, 其中以w,b为变量
将它作为原始最优化问题, 应用拉格朗日对偶性(Lagrange Duality), 通过求对偶问题(dual problem)得到原始问题的最优解[1]
其实我也是从这里第一次接触二次规划的概念, 在没有不等式的条件下, 形式和我们高数学过的多元函数求简单极值一样, 即是求闭区域内连续有界多元函数的驻点或偏导不存在点
条件极值下, 就要引入拉格朗日乘子, 印象求解过程很麻烦
求对偶问题
如下构造拉格朗日方程 L(w,b,α), 引入了拉格朗日乘子α









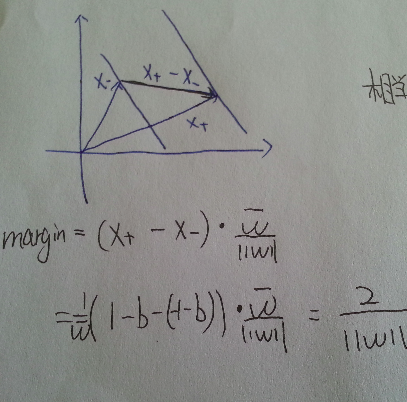
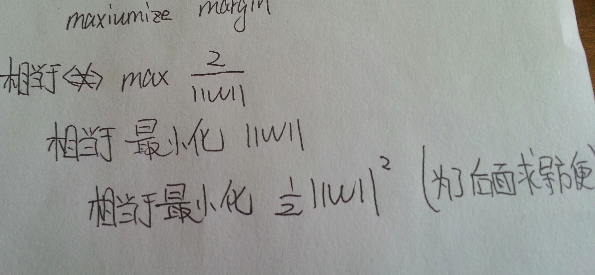
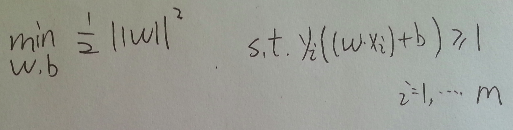
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








