斐波那契数列和矩阵的特征值于特征向量的关系&尾递归

置顶 papaofdoudou

已于 2025-02-28 08:13:27 修改

阅读量3.3k

点赞数 12

分类专栏：算法人工智能数学文章标签：线性代数算法

于 2021-10-08 23:17:59 首次发布

本文链接：https://blog.csdn.net/tugouxp/article/details/120660974

版权

人工智能同时被 3 个专栏收录

155 篇文章

订阅专栏

数学

151 篇文章

订阅专栏

算法

103 篇文章

订阅专栏

本文通过计算斐波那契数列相邻项的比值，发现了与黄金分割数的关联，并通过矩阵特征值理论进行理论证明。通过优化的通项公式，显著提升了计算效率。文章探讨了递归、尾递归、迭代以及矩阵理论在理解和优化计算过程中的作用，揭示了数学在编程中的美妙应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

从事软件开发的人对斐波那契数列可以说在熟悉不过了，一般是学习递归算法的入门案例写在教科书中，它用递推公式表达是这个样子的：

$F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)$

作为一名自尊自爱的码农，看到这个公式不免既心痒又难骚，必须要安排它一下，就拿相邻项的比值开刀，代码如下：

#include <stdio.h>
#include <stdlib.h>

long long feibonaqie(int n)
{
	if(n == 0)
		return 0;
	if(n == 1)
		return 1;

	return feibonaqie(n-1) + feibonaqie(n-2);
}

int main(void)
{
	int i;
	long long pre, cur;
	double portion;
	
	for(i = 0; i < 100; i ++)
	{
 		pre = cur;
		cur = feibonaqie(i);
 		if(i >= 2)
		{
			portion = (float)cur/(float)pre;
		}

		printf("feibonaqie(%d) = %lld.portion = %f\n", i, cur, portion);
	}

	return 0;
}

例子很简单，程序试图获取斐波那契数列前100项的值，常规的通过递归逻辑获取数列第N项值相信大家都能看懂，略去不讲。这里主要讲添加的一个自定义逻辑，它就是在计算的过程中，我们顺便计算了一下当前项和它前面一项的比值，并打印出来，这一打印，发现了一个奇特的规律：

上面的程序在我的电脑上执行到前50项时，花了半个钟的时间，简直是龟速，照这个速度，有生之年是看不到程序结束的了，不过即便如此，根据前50项的计算结果，貌似符合下面的规律：

$\lim_{n\rightarrow \infty }\frac{F(n)}{F(n-1)}=1.618034$

这个值可不普通，它的倒数是著名的黄金分割数，该如何证明呢?

数学最令人感到奇妙的是，在看似完全不相关的问题之间，竟然隐藏着自然而又出乎意料的关系，以这个问题为例，这个结论竟然可以通过线性代数中的矩阵特征向量和特征值的概念来解释。

我们先从从直观上解释，为什么这个结果是符合直觉的，然后在进行理论推导。

首先，我们换一种形式来表达上面的递推公式：

由于

$F(n)=F(n-1)+F(n-2), F(n-1)=F(n-1)$

所以我们可以将递推公式写成矩阵形式：

$\begin{bmatrix} F(n)\\ F(n-1) \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}\begin{bmatrix} F(n-1)\\ F(n-2) \end{bmatrix}$

我们仔细观察，看到两边的列向量具有相同的结构，都符合数列相连的前后项形式，既然是直观解释并非理论证明，我们先假设极限

$\lim_{n\rightarrow \infty }\frac{F(n)}{F(n-1)}$

存在，并且其值为 $\lambda$ ：

所以：

$\\ \lim_{n\rightarrow \infty }\frac{F(n)}{F(n-1)}= \lim_{n\rightarrow \infty }\frac{F(n-1)}{F(n-2)}=\lambda$

则，矩阵形式可以改写为：

$\begin{bmatrix} \lambda F(n-1)\\ F(n-1) \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}\begin{bmatrix} \lambda F(n-2)\\ F(n-2) \end{bmatrix}=>F(n-1) \begin{bmatrix} \lambda \\ 1 \end{bmatrix}=F(n-2)\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}\begin{bmatrix} \lambda \\ 1 \end{bmatrix}$

$\\F(n-1) \begin{bmatrix} \lambda \\ 1 \end{bmatrix}=F(n-2)\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}\begin{bmatrix} \lambda \\ 1 \end{bmatrix}=>\frac{F(n-1)}{F(n-2)}\begin{bmatrix} \lambda \\ 1 \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}\begin{bmatrix} \lambda \\ 1 \end{bmatrix}=\\ \lambda\begin{bmatrix} \lambda \\ 1 \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}\begin{bmatrix} \lambda \\ 1 \end{bmatrix}$

两边取极限，最后等式化为了

$\\ \lambda\begin{bmatrix} \lambda \\ 1 \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}\begin{bmatrix} \lambda \\ 1 \end{bmatrix}$

到了这里，相信你已经想起了什么，没错，这个形式是多么的像矩阵的特征值和特征向量的定义式:

$A\vec{x}=\lambda\vec{x}$

只要矩阵

$\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}$

的特征值恰好是特征向量第一个元素和第二个元素的比值，一切就会完美符合！

我们看一下是这样吗？

用octave求得此矩阵的特征向量和特征值：

可以看到，此矩阵有两个特征值，分别为-0.61803和1.61803，它们对应的特征向量分别为：

$\begin{bmatrix} 0.52573\\ -0.85065 \end{bmatrix}$

$\begin{bmatrix} -0.85065\\ -0.52573 \end{bmatrix}$

它们恰好满足

0.52573/-0.85065=-0.61803

-0.85065/-0.52573=1.6180

黄金分割等于1.618033....，它的倒数恰好等于它的小数部分，也就是：

$\frac{1}{x}=x-1$

由于斐波那契数列是逐项递增的，所以结果是特征值1.61803对应的特征向量，这也完美符合上面程序的打印，这并不是巧合，冥冥中隐藏了某种奥秘，通过这种方式，我们揭开了它的一角。

如果修改一下极限的定义形式，将极限定义为

$\lim_{n\rightarrow \infty }\frac{F(n-1)}{F(n)}$

这个时候，就是 -0.61803对应的特征值和特征向量了，所以，1.61803并没有什么特殊的，只是比值的顺序不同而已。

这个证明过程依赖直觉，不够严密，事不宜迟，下面用更加严谨的方式来证明这个结论。

理论证明：

首先计算矩阵A的特征值以及特征值对应的特征向量:

$A=\begin{bmatrix} 1& 1\\ 1 & 0 \end{bmatrix}$

$\left | A-\lambda I \right | = \begin{vmatrix} 1-\lambda& 1\\ 1 & -\lambda \end{vmatrix}=\lambda^2-\lambda-1=0$

所以：

$\lambda_1=\frac{1-\sqrt{5}}{2}\approx -0.618, \lambda_2=\frac{1+\sqrt{5}}{2}\approx 1.618$

$\lambda_1$ 对应的特征向量是

$\begin{bmatrix} \lambda_1\\ 1 \end{bmatrix}=\begin{bmatrix} \frac{1-\sqrt{5}}{2}\\ 1 \end{bmatrix}\approx \begin{bmatrix} -0.618\\ 1 \end{bmatrix}$

$\begin{bmatrix} \lambda_2\\ 1 \end{bmatrix}=\begin{bmatrix} \frac{1+\sqrt{5}}{2}\\ 1 \end{bmatrix}\approx \begin{bmatrix} 1.618\\ 1 \end{bmatrix}$

根据线性代数理论，属于不同特征值的特征向量线性无关，而线性无关的特征向量的线性组合一定可以表示整个平面，所以，斐波那契数列的初始项一定也可以由这两个特征向量来表示，也就是

$\begin{bmatrix} 1\\ 0\end{bmatrix}=c_1\begin{bmatrix} \frac{1-\sqrt{5}}{2}\\ 1\end{bmatrix}+c_2\begin{bmatrix} \frac{1+\sqrt{5}}{2}\\ 1\end{bmatrix}$

求解上面的二元一次方程，得到：

$c_1=-\frac{\sqrt{5}}{5},c_2=\frac{\sqrt{5}}{5}$

所以，斐波那契数列的递推公式也可以表达为：

$\begin{bmatrix} F(n)\\ F(n-1) \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}\begin{bmatrix} F(n-1)\\ F(n-2) \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}^2\begin{bmatrix} F(n-2)\\ F(n-3) \end{bmatrix}=\cdots=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}^{n-1}\begin{bmatrix} F(1)\\ F(0) \end{bmatrix}$

所以

$\begin{bmatrix} F(n)\\ F(n-1) \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}^{n-1}\begin{bmatrix} F(1)\\ F(0) \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}^{n-1}\bigg\{c_1\begin{bmatrix} \frac{1-\sqrt{5}}{2}\\ 1\end{bmatrix}+c_2\begin{bmatrix} \frac{1+\sqrt{5}}{2}\\ 1\end{bmatrix}\bigg\}$

所以：

$\\ \begin{bmatrix} F(n)\\ F(n-1) \end{bmatrix}=\frac{\sqrt{5}}{5}\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}^{n-1}\bigg\{\begin{bmatrix} \frac{1+\sqrt{5}}{2}\\ 1\end{bmatrix}-\begin{bmatrix} \frac{1-\sqrt{5}}{2}\\ 1\end{bmatrix}\bigg\} \\=\frac{\sqrt{5}}{5}\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}^{n-1}\begin{bmatrix} \frac{1+\sqrt{5}}{2}\\ 1\end{bmatrix}-\frac{\sqrt{5}}{5}\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}^{n-1}\begin{bmatrix} \frac{1-\sqrt{5}}{2}\\ 1\end{bmatrix}$

因为：

$A\vec{x}=\lambda\vec{x},A^2\vec{x}=\lambda^2\vec{x},\cdots, A^n\vec{x}=\lambda^n\vec{x}$

所以：

$\\ \begin{bmatrix} F(n)\\ F(n-1) \end{bmatrix}=\frac{\sqrt{5}}{5}\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}^{n-1}\begin{bmatrix} \frac{1+\sqrt{5}}{2}\\ 1\end{bmatrix}-\frac{\sqrt{5}}{5}\begin{bmatrix} 1 & 1\\ 1& 0 \end{bmatrix}^{n-1}\begin{bmatrix} \frac{1-\sqrt{5}}{2}\\ 1\end{bmatrix} = \\\frac{\sqrt{5}}{5}\lambda^{n-1}_2\begin{bmatrix} \frac{1+\sqrt{5}}{2}\\ 1\end{bmatrix}-\frac{\sqrt{5}}{5}\lambda^{n-1}_1\begin{bmatrix} \frac{1-\sqrt{5}}{2}\\ 1\end{bmatrix}=\frac{\sqrt{5}}{5}{(\frac{1+\sqrt{5}}{2})}^{n-1}\begin{bmatrix} \frac{1+\sqrt{5}}{2}\\ 1\end{bmatrix}-\frac{\sqrt{5}}{5}{(\frac{1-\sqrt{5}}{2})}^{n-1}\begin{bmatrix} \frac{1-\sqrt{5}}{2}\\ 1\end{bmatrix}$

所以，通过求解矩阵的特征值和特征向量，我们竟然得到了斐波那契数列的通项公式！

$F(n)=\frac{\sqrt{5}}{5}{(\frac{1+\sqrt{5}}{2})}^{n-1}\frac{1+\sqrt{5}}{2}-\frac{\sqrt{5}}{5}{(\frac{1-\sqrt{5}}{2})}^{n-1}\frac{1-\sqrt{5}}{2}$

化简后得到通项公式：

$F(n)=\frac{\sqrt{5}}{5}\bigg[{(\frac{1+\sqrt{5}}{2})}^{n}-{(\frac{1-\sqrt{5}}{2})}^{n}\bigg]$

真是大大的惊喜，大大的意外!

而且，关于为何初始向量

$\begin{bmatrix} 1\\ 0\end{bmatrix}$

不在特征向量的方向上，仍然最后收敛于特征向量，也得到了解释，通过通项公式可以看出，随着n的增大，

${(\frac{1-\sqrt{5}}{2})}^{n}$

所代表的项目由于特征值小于1，会逐渐趋近于0，只剩下特征值1.618对应的特征向量，所以最后显露出来的，是特征值 $\lambda_2$ 代表的特征， $\lambda_1$ 的特征会逐渐消失。

原理上，斐波纳契数列应该和2为底的指数函数比较接近，下面的图形证明了这个说法。

在控制科学领域， $\lambda_2$ 为对应稳态分量， $\lambda_1$ 对应暂态分量，随着次数逐渐升高， $\lambda_1$ 对应项逐渐收敛为０，仅仅剩下稳态分量和稳态分量对应的稳态向量，这也是上面的推导过程证明的结论。

从上面的理论推导结果我们还可以得到一个推论，就是斐波那契数列的相邻项比值的极限，和初始向量的定义无关，比如，我们随便修改一下初始条件为：

$\begin{bmatrix} F(1)\\ F(0)\end{bmatrix}=\begin{bmatrix} 8\\ 9\end{bmatrix}$

计算最终极限仍然是1.618034

斐波那契数列，竟然通过相邻项求比值的方式，和矩阵的特征值和特征向量建立了联系，让人不得惊叹于数学的奇妙。

斐波那契数列将遵循这个趋势，这个趋势就是当前项是前一项的1.61804倍，随着N的增加，这个比例会越来越精确，F(n),F(n-1)构成的列向量会越来越接近1.61804对应的特征向量，我们可以通过这种方式来计算下一位的值，毕竟收限于算力，对于普通的PC来说，想要计算斐波那契数列的前100项的值，也是难如登天的一件事情。

写这篇文章花了1个小时，在这1个小时的时间里，程序又算出了5项数列的值

这是运行一夜的情况，四核八线程I5，一个晚上仅仅算出来56，57，58，59四项的值。

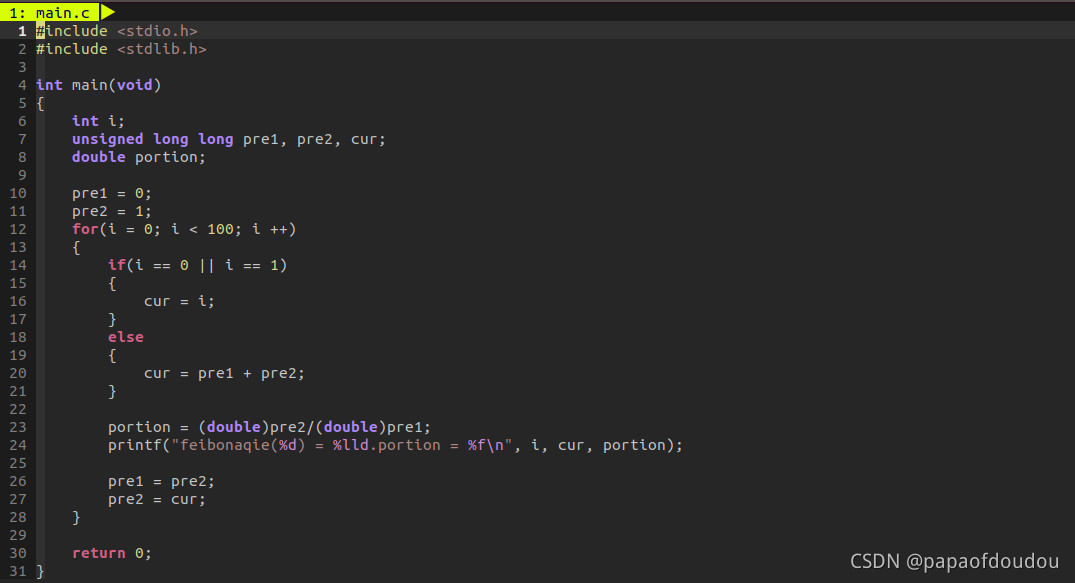
既然已经找到了通项公式，接下来我们用通项公式来计算斐波那契数列前100项的值，代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

unsigned long long febnaqi(int n)
{
	double sqrt5=sqrt(5.00);
	double vec1 = (1 + sqrt5)/2;
	double vec2 = (1 - sqrt5)/2;

	return (sqrt5/5) * (pow(vec1, n)-pow(vec2,n));
}

int main(void)
{
	int i;
	
	for(i = 0; i < 100; i ++)
	{
		printf("febnaqi(%d)=%llu.\n", i, febnaqi(i));
	}

	return 0;
}

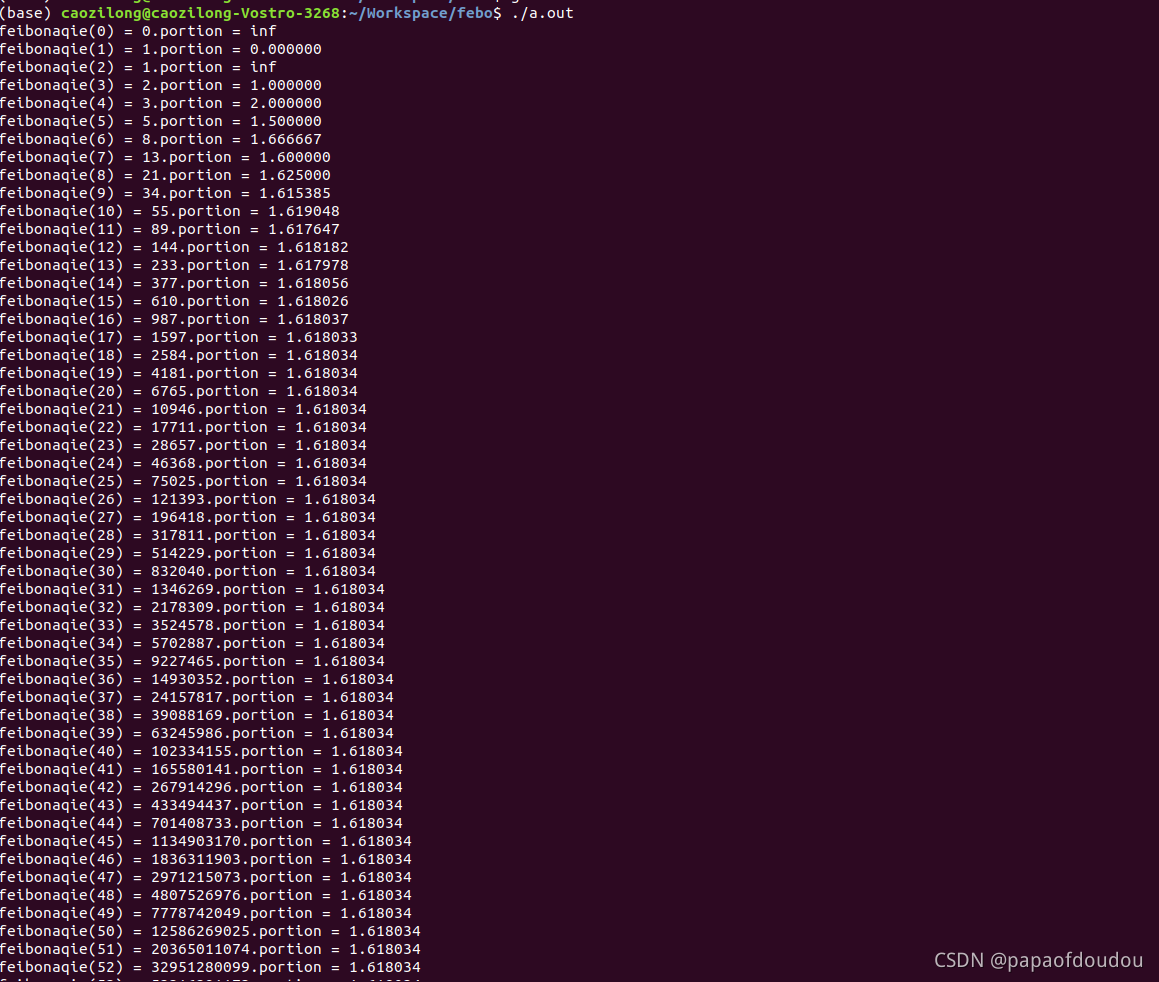
运行结果如下，最后94-99已经溢出，无法的到正确的值，从程序开始运行到执行结束，也就一眨眼的事，可以看到，我们推导除了斐波那契数列的通项公式后，大大加速了我们的计算效率，这也是为什么好的算法如此重要的原因。

czl@czl-VirtualBox:~/WorkSpace$ ./a.out 
febnaqi(0)=0.
febnaqi(1)=1.
febnaqi(2)=1.
febnaqi(3)=2.
febnaqi(4)=3.
febnaqi(5)=5.
febnaqi(6)=8.
febnaqi(7)=13.
febnaqi(8)=21.
febnaqi(9)=34.
febnaqi(10)=55.
febnaqi(11)=89.
febnaqi(12)=144.
febnaqi(13)=233.
febnaqi(14)=377.
febnaqi(15)=610.
febnaqi(16)=987.
febnaqi(17)=1597.
febnaqi(18)=2584.
febnaqi(19)=4181.
febnaqi(20)=6765.
febnaqi(21)=10946.
febnaqi(22)=17711.
febnaqi(23)=28657.
febnaqi(24)=46368.
febnaqi(25)=75025.
febnaqi(26)=121393.
febnaqi(27)=196418.
febnaqi(28)=317811.
febnaqi(29)=514229.
febnaqi(30)=832040.
febnaqi(31)=1346269.
febnaqi(32)=2178309.
febnaqi(33)=3524578.
febnaqi(34)=5702887.
febnaqi(35)=9227465.
febnaqi(36)=14930352.
febnaqi(37)=24157817.
febnaqi(38)=39088169.
febnaqi(39)=63245986.
febnaqi(40)=102334155.
febnaqi(41)=165580141.
febnaqi(42)=267914296.
febnaqi(43)=433494437.
febnaqi(44)=701408733.
febnaqi(45)=1134903170.
febnaqi(46)=1836311903.
febnaqi(47)=2971215073.
febnaqi(48)=4807526976.
febnaqi(49)=7778742049.
febnaqi(50)=12586269025.
febnaqi(51)=20365011074.
febnaqi(52)=32951280099.
febnaqi(53)=53316291173.
febnaqi(54)=86267571272.
febnaqi(55)=139583862445.
febnaqi(56)=225851433717.
febnaqi(57)=365435296162.
febnaqi(58)=591286729879.
febnaqi(59)=956722026041.
febnaqi(60)=1548008755920.
febnaqi(61)=2504730781961.
febnaqi(62)=4052739537881.
febnaqi(63)=6557470319842.
febnaqi(64)=10610209857723.
febnaqi(65)=17167680177565.
febnaqi(66)=27777890035288.
febnaqi(67)=44945570212853.
febnaqi(68)=72723460248141.
febnaqi(69)=117669030460994.
febnaqi(70)=190392490709135.
febnaqi(71)=308061521170129.
febnaqi(72)=498454011879265.
febnaqi(73)=806515533049395.
febnaqi(74)=1304969544928660.
febnaqi(75)=2111485077978055.
febnaqi(76)=3416454622906716.
febnaqi(77)=5527939700884771.
febnaqi(78)=8944394323791489.
febnaqi(79)=14472334024676262.
febnaqi(80)=23416728348467748.
febnaqi(81)=37889062373144008.
febnaqi(82)=61305790721611760.
febnaqi(83)=99194853094755776.
febnaqi(84)=160500643816367552.
febnaqi(85)=259695496911123360.
febnaqi(86)=420196140727490944.
febnaqi(87)=679891637638614400.
febnaqi(88)=1100087778366105216.
febnaqi(89)=1779979416004719616.
febnaqi(90)=2880067194370825216.
febnaqi(91)=4660046610375545856.
febnaqi(92)=7540113804746370048.
febnaqi(93)=12200160415121915904.
febnaqi(94)=0.
febnaqi(95)=0.
febnaqi(96)=0.
febnaqi(97)=0.
febnaqi(98)=0.
febnaqi(99)=0.
czl@czl-VirtualBox:~/WorkSpace$

初始的程序版本使用的是尾递归的形式，尾递归是指在最后一行的递归调用，并且递归调用语句只有一个,由于是最后一行的调用，这时候的栈帧临时存储不具有保存价值，所以，除了形式上的简明之外，递归失去了意义，这种结构的递归不需要使用栈即可用迭代法或者辗转法消除，并且斐波那契数列并不适合使用递归方法，后面会解释。

辗转法消除递归的程序版本：

另一个用空间换时间策略的实现版本，由于使用了数组预分配空间，不需要辗转赋值：

运行结果：

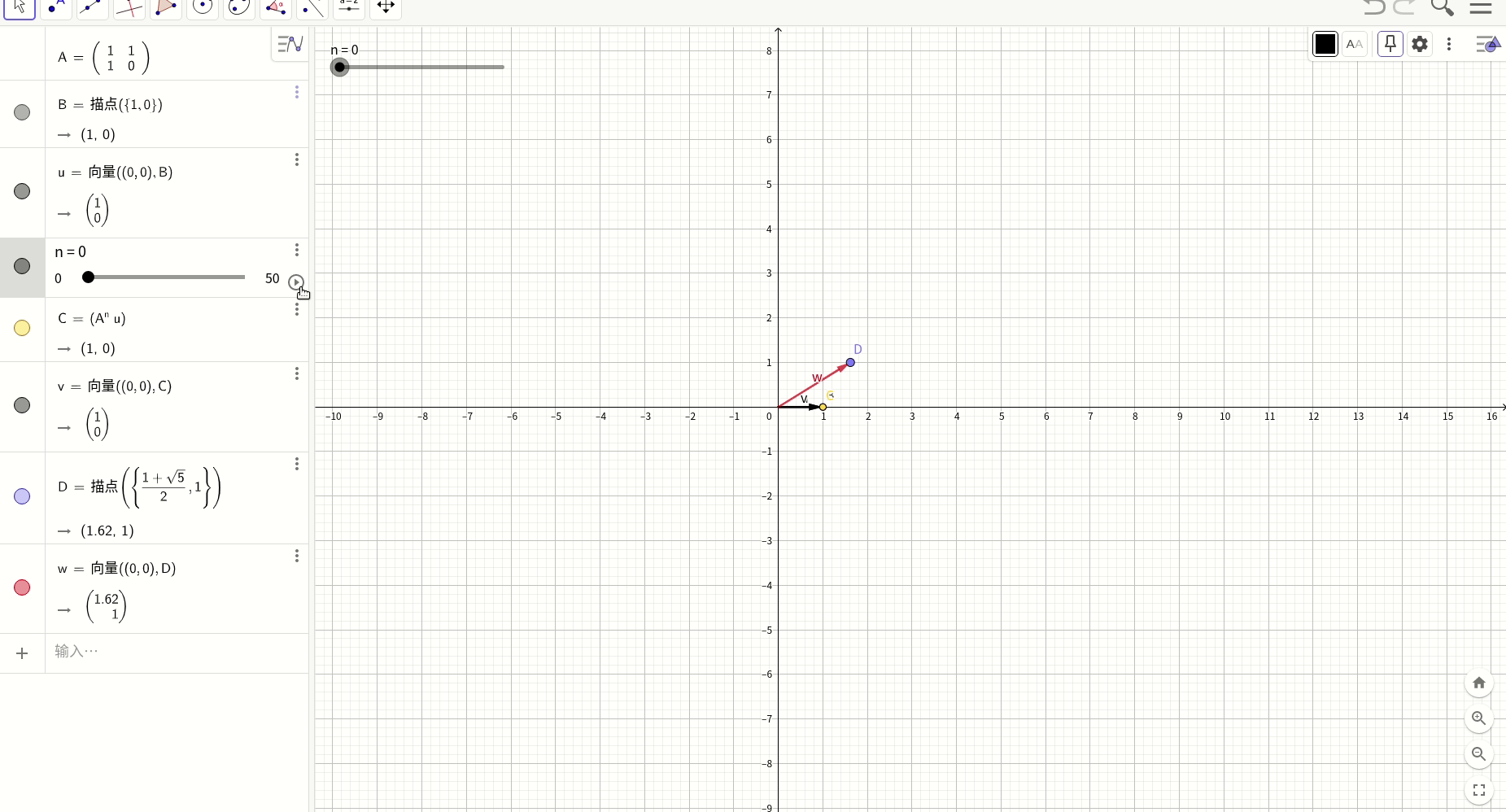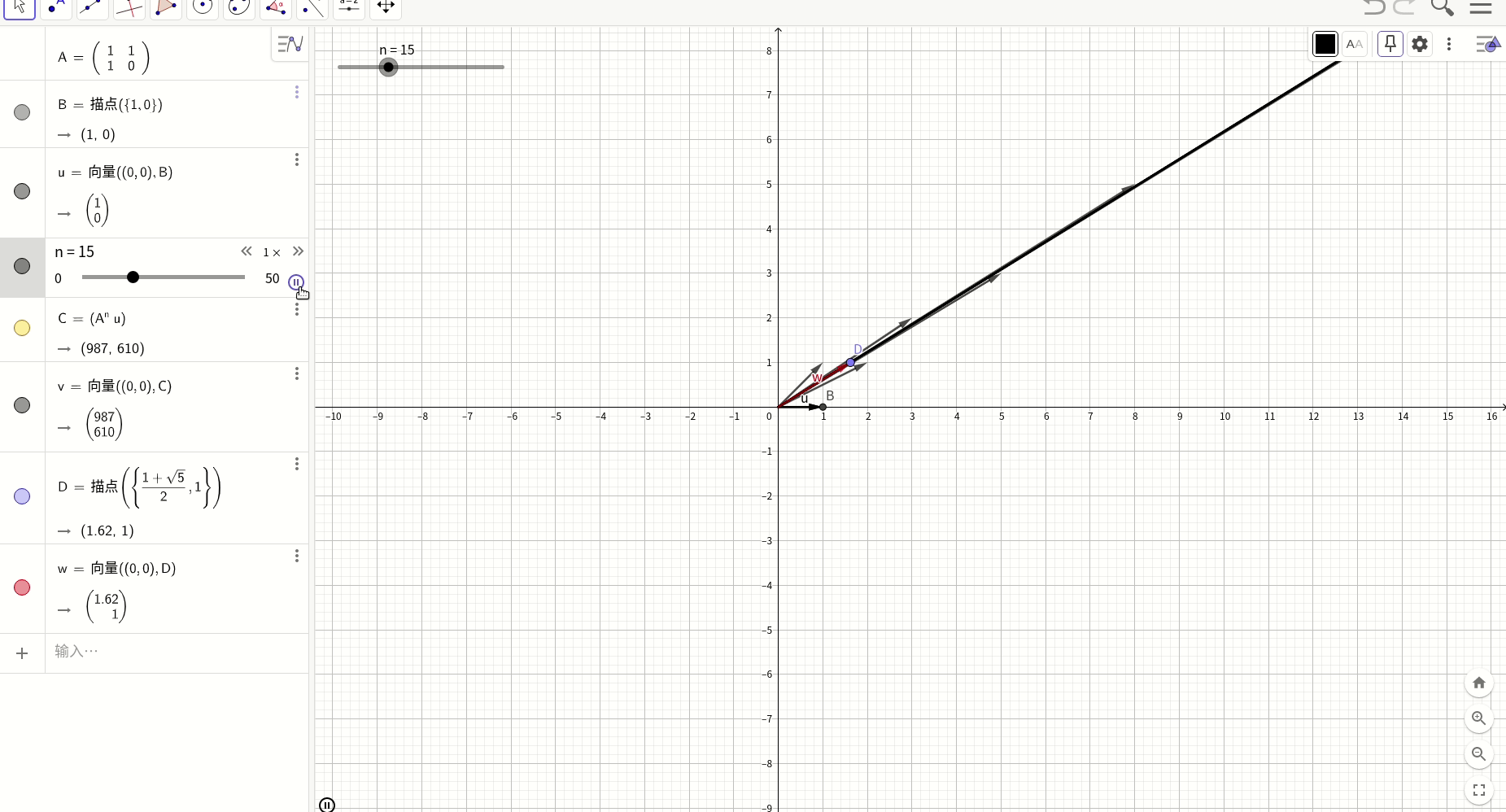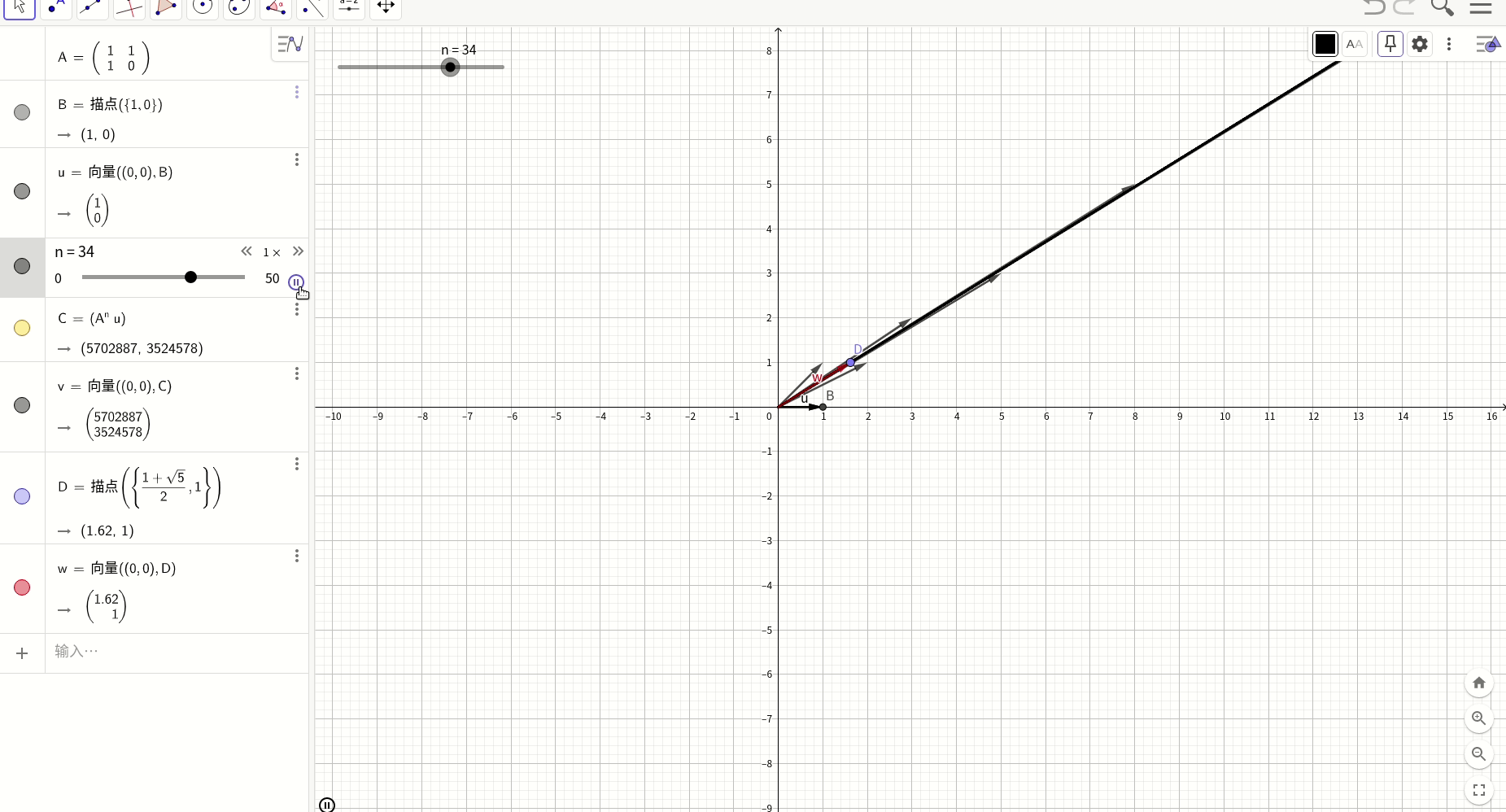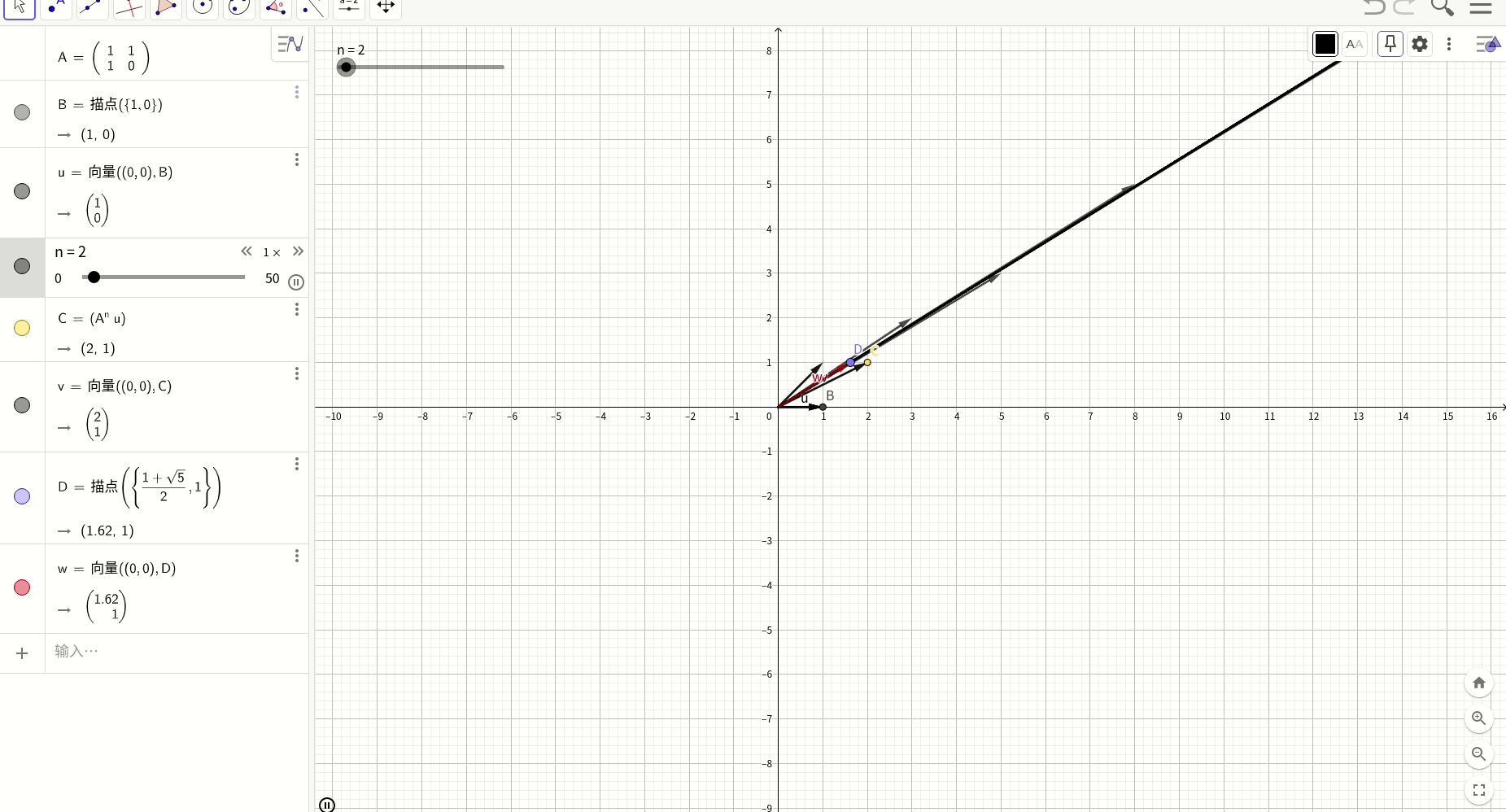
图形化表述：

我们用geogebra工具图形化表述上述过程，红色的向量是 $\lambda_2$ 对应的特征向量，其斜率是黄金分割率0.618，而黑色的向量则是斐波那契数列的初始条件向量，随着N的递增，经过变换后的向量最终越来越趋近于特征向量的方向，这就是上述过程的图形化表述。

斐波那切数列应用

斐波那契数列的图形化展示，下图表示以斐波那契数列为班级的四分之一向外扩散的圆弧形态：

自然界中符合斐波那契数列形态的身影随处可见，比如海螺壳：

葵花子的花盘，台风的形态等：

递归和尾递归

在计算机编程实现中有常常两种方法：一为迭代（iterate）；二为递归（recursion).
迭代是利用已知的变量值，根据递推公式不断演进得到变量新值得编程思想。递归则是指程序调用自身的编程思想，即一个函数调用本身。

如果递归是自己调用自己的话,迭代就是A不停的调用B。
从直观上讲，递归是将大问题化为相同结构的小问题，从待求解的问题出发，一直分解到已经已知答案的最小问题为止，然后再逐级返回，从而得到大问题的解（一个非常形象的例子就是分类回归树 classification and regression tree，从root出发，先将root分解为另一个(root,sub-tree)，就这样一直分解，直到遇到leafs后逐层返回）；而迭代则是从已知值出发，通过递推式，不断更新变量新值，一直到能够解决要求的问题为止。

编译器对尾递归的支持

根据定义，函数返回的最后一个操作是递归调用时就被称作尾递归. 尾递归效率比普通递归高，原因是尾递归没有函数栈调用的开销，也就是是说编译器会将尾递归优化为非递归调用，当然者需要编译器的支持，gcc中控制此优化的选项为-foptimize-sibling-calls。

看一下优化前后的样子：

#include <stdio.h>
 
int jiecheng(int n)
{
	int res;
 
#if 1
	printf("%s line %d, n = %d addr(n) %p.\n", __func__, __LINE__, n, &n);
#else
	printf("%s line %d, n = %d.\n", __func__, __LINE__, n);
#endif
	if (n == 1) return 1;
 
	res = n*jiecheng(n-1);
 
//	printf("%s line %d, n = %d.\n", __func__, __LINE__, n);
 
	return res;
}
 
int main(void)
{
	int n = jiecheng(10);
 
	printf("%s line %d, n = %d.\n", __func__, __LINE__, n);
}

-O0选项编译，不启用尾递归优化，发现每次n的地址不一样，函数入口jiecheng被递归调用多次，说明函数栈被持续展开，仍然使用了递归。

使用尾递归优化编译gcc -O1 -g wei.c -foptimize-sibling-calls -o opt,发现仍然是递归调用，尾递归优化没有生效。

堆栈依赖：

上面优化失败的原因是堆栈依赖阻止了编译器的优化，下文的打印最后一个参考，取n的的地址，依赖于堆栈的扩展，否则优化后的上下文无法提供多个地址。

将#if 1修改为#if 0，使用下面的打印，这个时候就不依赖于堆栈了，再次进行实验，jiecheng函数仅仅进入一次，尾递归优化成功：

尾递归调用对递归调用之后的要求要高于递归调用前的要求，上面的实验，虽然不允许递归调用前的printf函数打印n的地址避免堆栈依赖，但是至少还可以打印n的值，但是递归调用后面就啥都不能做了，只能乖乖返回，否则，也会阻止编译器优化，比如下面我们在递归调用后面加一行无关打印，尾递归优化便无法进行了：

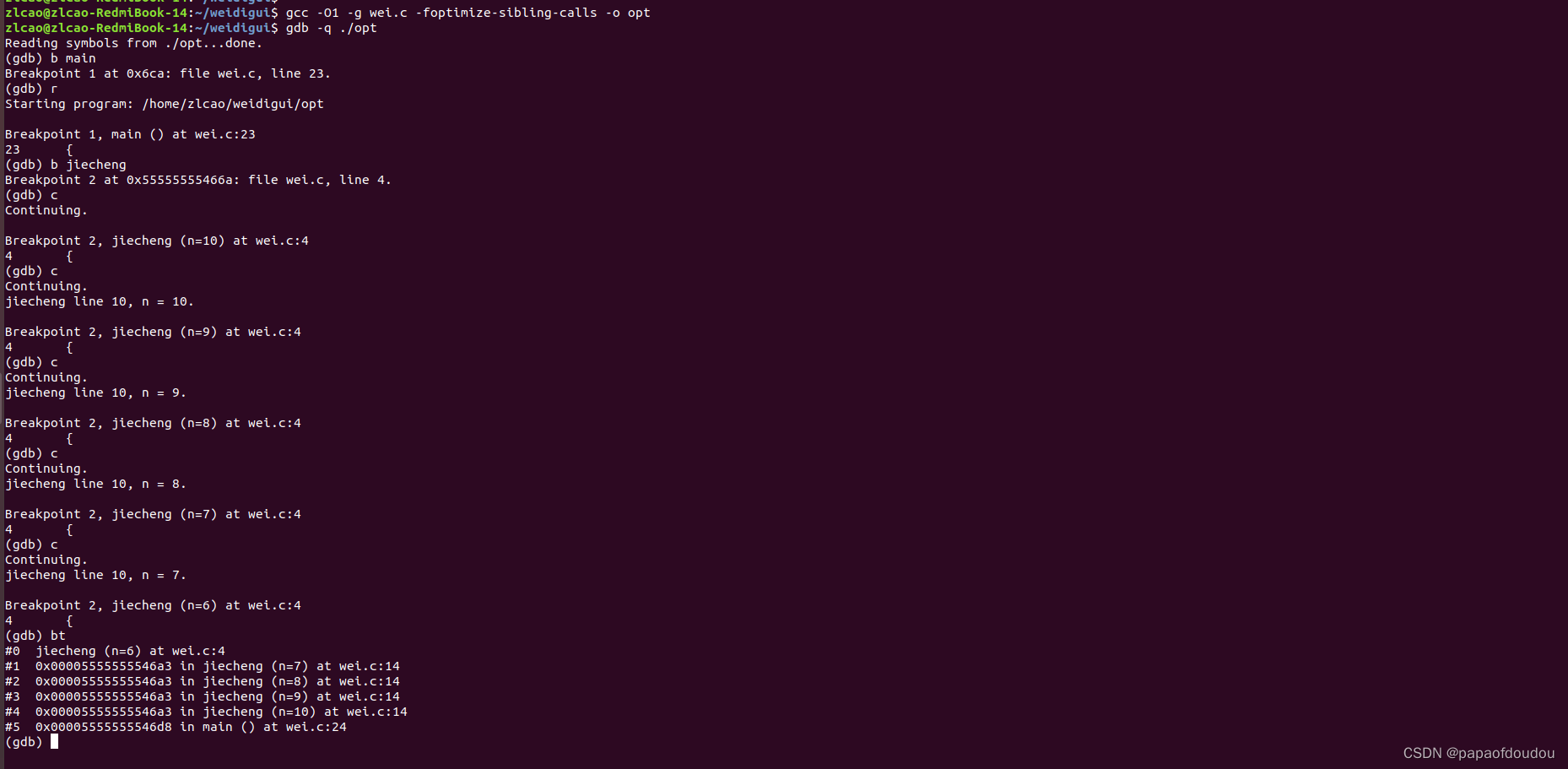
尾递归优化后，函数不再调用自身，看如下汇编指令，用ebp寄存器保存当前阶乘结果，用ebx保存当前的N值，当完成当前的计算后，jmp回再次计算N-1时的阶乘，直到保存当前N值的寄存器等于1时退出到6aa。

所以，尾递归要求的条件总结如下：

1.递归调用后立刻返回。2.递归调用前没有阻挠尾递归优化的堆栈依赖。

经过尾递归优化后，函数性能通常会变的更好，不会出现内存溢出的问题，节省内存使用。

从这个角度来说，本篇开头那段斐波那切实现不算是尾递归，因为它通常会使用两个递归调用，并且在返回之前需要将这两个调用的结果相加。需要堆栈提供临时空间保存中间结果，所以构成了堆栈依赖。

在本文开头的递归实现中，每次递归调用都会调用两次递归，分别是 fibonacci(n-1) 和 fibonacci(n-2)，然后将它们的结果相加。这个过程不是尾递归，因为在返回之前需要将两个递归调用的结果相加。

尾递归的特点是在递归函数的最后一步执行递归调用，而不需要在返回之前进行额外的操作。要将斐波那契数列的计算实现为尾递归，可以使用一个辅助函数来累积结果。以下是一个尾递归版本的斐波那契数列计算函数：

#include <stdio.h>
#include <stdlib.h>
 
long long feibonaqie(int n, int current, int next)
{
	if(n == 0)
		return current;
 
	return feibonaqie((n-1), next, current + next);
}
 
int main(void)
{
	int i;
	long long pre, cur;
	double portion;
	
	for(i = 0; i < 46; i ++)
	{
 		pre = cur;
		cur = feibonaqie(i, 0, 1);
 		if(i >= 2)
		{
			portion = (float)cur/(float)pre;
		}
 
		printf("feibonaqie(%d) = %lld.portion = %f\n", i, cur, portion);
	}
 
	return 0;
}

在这个尾递归版本中，递归调用是在最后一步执行的，不需要在返回之前进行额外的操作。这使得函数具有尾递归的特性。此版本可以更有效地处理较大的斐波那契数列值，因为它不会导致栈溢出，并且在某些编程语言和编译器中可以进行尾递归优化。

另外，尾递归和是否能够非递归化是两回事，所有的递归函数都可以非递归化，但不是所有的递归都是尾递归，并且，现阶段，只有尾递归可以由编译器非递归优化，而其它行使的递归，除了手动非递归优化之外，智能通过先尾递归再编译器优化尾递归的方式进行优化。

最规范的尾递归-尾调用递归

如果一个函数的最后一步是调用一个函数，尾调用是指函数调用出现在调用者函数的最后，并且该调用的返回值直接被当前函数返回，如果尾调用的函数是自身则这种调用是最为规范的尾递归，编译器可以直接进行优化处理。

WIKI百科对尾调用的解释：尾调用是指一个函数里的最后一个动作是一个函数调用的情形：即这个调用的返回值直接被当前函数返回的情形。这种情形下称该调用位置为尾位置。若这个函数在尾位置调用本身（或是一个尾调用本身的其他函数等等），则称这种情况为尾递归，是递归的一种特殊情形。

比如，下面这个是尾调用：

return f();

而这个不是：

return 1 + f();

关于尾调用，有个重要的优化叫做尾调用消除。经过尾调用消除优化后的程序在执行尾调用时不会导致调用栈的增长。其实，这个优化可能不算是优化。因为在某些计算模型中，尾调用天然不会导致调用栈的增长。在EOPL(ssentials of Programming Language)提到过一个原理：

导致调用栈增长的，是对参数的计算，而不是函数调用。

由于尾调用不会导致调用栈的增长，所以尾调用事实上不像函数调用，而更接近GOTO。尾递归则等同于迭代，只是写法上的不同罢了。

#include <stdio.h>
 
#if 0
int jiecheng(int n)
{
	int res;
 
	if (n == 1) return 1;
 
	return n*jiecheng(n-1);
}
#else
int jiecheng(int n, int res)
{
	if (n == 0) return 1;
	if (n == 1) return res;
 
	return jiecheng(n-1, res * n);
}
#endif
 
int main(void)
{
	int n = jiecheng(10, 1);
 
	printf("%s line %d, n = %d.\n", __func__, __LINE__, n);
}

斐波那切数列的尾递归实现，基本上，可以用循环实现的结构，也可以用尾递归实现，反之亦然。

#include <stdio.h>
#include <stdlib.h>

unsigned long fabinaci(int n)
{
    int a = 0, b = 1;
    int sum = 0;

    while(n >= 2) {
	sum = a + b;
	a = b;
	b = sum;
	n --;
    }

    return sum;
}

unsigned long fabinaci_digui(int n, int a, int b)
{
    int sum;
    sum = a+b; 

    if(n == 2) return sum;

    return fabinaci_digui(-- n, b, sum);
}

int main(void)
{
    printf("%s line %d, fab(13) = %ld.\n", __func__, __LINE__, fabinaci(13));
    printf("%s line %d, fab(13) = %ld.\n", __func__, __LINE__, fabinaci_digui(13, 0, 1));

    return 0;
}

如何思考递归

递归不但可以使计算机的堆栈爆掉，也会让我们的大脑爆炸，合理的方法是将递归和自然数联系在一起，从递归的第一步，自然数0开始考虑递归，第一不需要递归，所以可以集于此构建递归大厦。

递归（recursion）是一种算法策略，通过直接或者间接地调用自身来解决问题，将大问题分解成更多的子问题，主要解决同一大类问题。

递归过程主要包含两个阶段：

递：程序不断深入地调用自身，通常传入更小或更简化的参数，直到达到“终止条件”。
归：触发“终止条件”后，程序从最深层的递归函数开始逐层返回，汇聚每一层的结果。

递可以理解为“传递”是迭代的逆过程，归可以理解为“回归”是一个正像迭代的过程，人类的大脑善于理解“回归"过程，但是理解“传递”的过程比较费力。从这个角度看，尾递归就是那种"递"的过程已经解决了所有问题，不需要"归"阶段的一种递归形式。

无限递归和有限递归/递归构造

世界上存在无限递归，比如门特波罗佛，谢尔宾斯基三角形，科赫雪花，海岸线地图等分形图，无限递归的过程只有“递”，没有“归”，在"递"的过程中就把问题解决了。计算机能够处理的是有穷递归，包含“递"和“归"两个过程。

一个用递归实现的内存拷贝：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define RECURSIVE_SIZE   8
void memcpy_recursive(void *dst, void *src, int n)
{
    if (n <= 4) {
	memcpy(dst, src, n);
    } else {
	memcpy(dst, src, RECURSIVE_SIZE);
	memcpy_recursive(dst + RECURSIVE_SIZE, src + RECURSIVE_SIZE, n - RECURSIVE_SIZE);
    }
}

int main(void)
{
    char *src = "hello word, i miss you very much and i am very like you, could you help me on this, i am a engineer.";
    char dst[1024];

    memcpy_recursive(dst, src, strlen(src));

    printf("%s line %d, dst %s\n", __func__, __LINE__, dst);
    return 0;
}

平方递归

#include <stdio.h>
#include <stdlib.h>

int pingfang(int n)
{
    if (n == 1)
	return 1;
    else
	return pingfang(n-1) + 2*(n-1) + 1;
}

int main(void)
{
    printf("%s line %d, pintfang(5) = %d.\n", __func__, __LINE__, pingfang(5));
    return 0;
}

#include <stdio.h>
#include <stdlib.h>

int pingfang(int n)
{
    if((n % 2) == 0) {
        printf("%s line %d, input should be odd.\n",
		__func__, __LINE__);
        return -1;
    }

    if (n == 1)
	return 1;
    else
	return pingfang(n-2) + (n);
}

int main(void)
{
    printf("%s line %d, pintfang(9) = %d.\n", __func__, __LINE__, pingfang(9));
    return 0;
}

经典递归算法-走出迷宫

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define SIZE  12

static int matrix[SIZE][SIZE];
struct pos {
	int x;
	int y;
};

int idx = 0;
struct pos stack[100];

void push_stack(int x, int y)
{
	struct pos tmp;

	tmp.x = x;
	tmp.y = y;

	stack[idx] = tmp;
	idx ++;
}

void pop_stack(void)
{
	idx --;
}
void init_matrix(int mtx[][SIZE])
{
	int i, j;

	for (i = 0; i < SIZE; i++) {
		for (j = 0; j < SIZE; j++) {
#if 0
			if (i == 0 || j == 0) {
				mtx[i][j] = 1;
				continue;
			} else if (i == SIZE - 1 || j == SIZE - 1) {
				mtx[i][j] = 1;
				continue;
			}
#else
			if (i != j && (i != j + 1))
				mtx[i][j] = 1;
#endif
		}
	}

	mtx[0][0] = mtx[11][11] = 1;
	mtx[1][0] = mtx[11][10] = 1;
	mtx[9][8] = 1;
	mtx[7][8] = 0;
	mtx[7][9] = 0;
	mtx[8][7] = 1;
	mtx[7][10] = 0;
	mtx[8][10] = 0;
	mtx[9][10] = 0;
	mtx[7][5] = 0;
	mtx[8][5] = 0;
	mtx[9][5] = 0;
	mtx[10][5] = 0;
}

void dump_matrix(int mtx[][SIZE])
{
	int i, j;

	for (i = 0; i < SIZE; i++) {
		for (j = 0; j < SIZE; j++) {
			printf("%d    ", mtx[i][j]);
		}
		printf("\n");
	}

	printf("\n");
	return;
}

//#define CASE1
//#define CASE2
int find_way(int x, int y, int mtx[][SIZE])
{
	int ret = -1;
#ifdef CASE2
	printf("(%d, %d)\n", x, y);
#endif

	push_stack(x, y);
	if (x == 10 && y == 10) {
		printf("found way.\n");
		dump_matrix(mtx);
		int j = 0;
		for (j = 0; j < idx; j ++) {
			printf("(%d, %d)\n", stack[j].x, stack[j].y);
		}
		//exit(-1);
		pop_stack();
		return 0;
	}

	if ((x < SIZE - 2) && !mtx[x + 1][y]) {
		mtx[x][y] = 1;
		ret = find_way(x + 1, y, mtx);
		if (ret) {
#ifdef CASE1
			//mtx[x + 1][y] = 1;
#endif
		} else {
#ifndef CASE2
			//printf("(%d, %d)\n", x, y);
#endif
		}
		mtx[x][y] = 0;
	}

	if ((y < SIZE - 2) && !mtx[x][y + 1]) {
		mtx[x][y] = 1;
		ret = find_way(x, y + 1, mtx);
		if (ret) {
#ifdef CASE1
			//mtx[x][y + 1] = 1;
#endif
		} else {
#ifndef CASE2
			//printf("(%d, %d)\n", x, y);
#endif
		}
		mtx[x][y] = 0;
	}

	if ((x > 1) && !mtx[x - 1][y]) {
		mtx[x][y] = 1;
		ret = find_way(x - 1, y, mtx);
		if (ret) {
#ifdef CASE1
			//mtx[x - 1][y] = 1;
#endif
		} else {
#ifndef CASE2
			//printf("(%d, %d)\n", x, y);
#endif
		}
		mtx[x][y] = 0;
	}

	if ((y > 1) && !mtx[x][y - 1]) {
		mtx[x][y] = 1;
		ret = find_way(x, y - 1, mtx);
		if (ret) {
#ifdef CASE1
			//mtx[x][y - 1] = 1;
#endif
		} else {
#ifndef CASE2
			//printf("(%d, %d)\n", x, y);
#endif
		}
		mtx[x][y] = 0;
	}
	pop_stack();
	if (ret) {
		//mtx[x][y] = 1;
	} else {
		//      printf("(%d, %d)\n", x, y);
	}
	//printf("(%d, %d)\n", x, y);

	return ret;
}

int main(void)
{
	memset(matrix, 0x00, SIZE * SIZE * sizeof(int));

	init_matrix(matrix);
	dump_matrix(matrix);

	find_way(1, 1, matrix);
	dump_matrix(matrix);

	return 0;
}

zlcao@zlcao-RedmiBook-14:~/Workspace/dumpstack/test/recursive$ ./a.out 
1    1    1    1    1    1    1    1    1    1    1    1    
1    0    1    1    1    1    1    1    1    1    1    1    
1    0    0    1    1    1    1    1    1    1    1    1    
1    1    0    0    1    1    1    1    1    1    1    1    
1    1    1    0    0    1    1    1    1    1    1    1    
1    1    1    1    0    0    1    1    1    1    1    1    
1    1    1    1    1    0    0    1    1    1    1    1    
1    1    1    1    1    0    0    0    0    0    0    1    
1    1    1    1    1    0    1    1    0    1    0    1    
1    1    1    1    1    0    1    1    1    0    0    1    
1    1    1    1    1    0    1    1    1    0    0    1    
1    1    1    1    1    1    1    1    1    1    1    1    

found way.
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    0    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    0    1    1    0    1    1    1    
1    1    1    1    1    0    1    1    1    0    1    1    
1    1    1    1    1    0    1    1    1    0    0    1    
1    1    1    1    1    1    1    1    1    1    1    1    

(1, 1)
(2, 1)
(2, 2)
(3, 2)
(3, 3)
(4, 3)
(4, 4)
(5, 4)
(5, 5)
(6, 5)
(7, 5)
(7, 6)
(7, 7)
(7, 8)
(7, 9)
(7, 10)
(8, 10)
(9, 10)
(10, 10)
found way.
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    0    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    0    1    1    0    1    1    1    
1    1    1    1    1    0    1    1    1    1    1    1    
1    1    1    1    1    0    1    1    1    1    0    1    
1    1    1    1    1    1    1    1    1    1    1    1    

(1, 1)
(2, 1)
(2, 2)
(3, 2)
(3, 3)
(4, 3)
(4, 4)
(5, 4)
(5, 5)
(6, 5)
(7, 5)
(7, 6)
(7, 7)
(7, 8)
(7, 9)
(7, 10)
(8, 10)
(9, 10)
(9, 9)
(10, 9)
(10, 10)
found way.
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    0    1    1    1    1    1    1    
1    1    1    1    1    0    1    1    0    1    1    1    
1    1    1    1    1    0    1    1    1    0    1    1    
1    1    1    1    1    0    1    1    1    0    0    1    
1    1    1    1    1    1    1    1    1    1    1    1    

(1, 1)
(2, 1)
(2, 2)
(3, 2)
(3, 3)
(4, 3)
(4, 4)
(5, 4)
(5, 5)
(6, 5)
(6, 6)
(7, 6)
(7, 7)
(7, 8)
(7, 9)
(7, 10)
(8, 10)
(9, 10)
(10, 10)
found way.
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    1    1    1    1    1    1    1    
1    1    1    1    1    0    1    1    1    1    1    1    
1    1    1    1    1    0    1    1    0    1    1    1    
1    1    1    1    1    0    1    1    1    1    1    1    
1    1    1    1    1    0    1    1    1    1    0    1    
1    1    1    1    1    1    1    1    1    1    1    1    

(1, 1)
(2, 1)
(2, 2)
(3, 2)
(3, 3)
(4, 3)
(4, 4)
(5, 4)
(5, 5)
(6, 5)
(6, 6)
(7, 6)
(7, 7)
(7, 8)
(7, 9)
(7, 10)
(8, 10)
(9, 10)
(9, 9)
(10, 9)
(10, 10)
1    1    1    1    1    1    1    1    1    1    1    1    
1    0    1    1    1    1    1    1    1    1    1    1    
1    0    0    1    1    1    1    1    1    1    1    1    
1    1    0    0    1    1    1    1    1    1    1    1    
1    1    1    0    0    1    1    1    1    1    1    1    
1    1    1    1    0    0    1    1    1    1    1    1    
1    1    1    1    1    0    0    1    1    1    1    1    
1    1    1    1    1    0    0    0    0    0    0    1    
1    1    1    1    1    0    1    1    0    1    0    1    
1    1    1    1    1    0    1    1    1    0    0    1    
1    1    1    1    1    0    1    1    1    0    0    1    
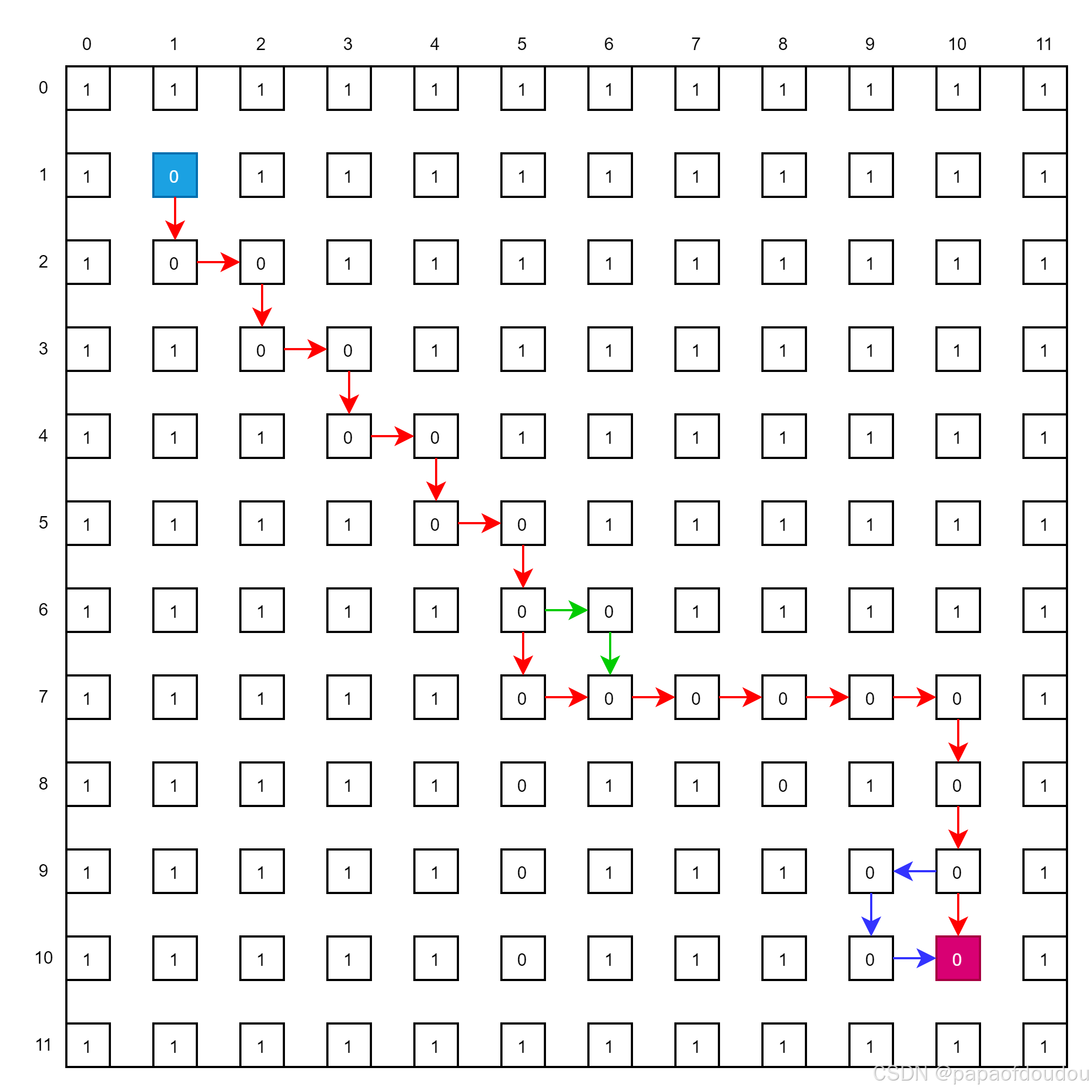
1    1    1    1    1    1    1    1    1    1    1    1

搜索出来四条走出迷宫的路径，如下图所示：

实现注意点：

1.为了避免陷入来回跳陷入死循环，在进入下一步递归搜索前，必须将当前位置设置为BLOCK，避免算法进入无穷抖动。

2.应该用四个方向上的if而非else if,因为递归过程中，四个方向都需要试探，而非四选1。

3.在达到出口时及时将路径打印出来，否则中间递归层可能遇到死胡同返回错误，影响堆栈中的正常路径的打印。

4.死胡同不需要设置不可走标志(设置为1)，因为每曾递归都是顺序走完四个方向，走过之后就不会再走了，标志没有用处。

总结：

理论推导的关键一步，是将初始向量表示为特征向量的线性组合，突破这一步，推导过程豁然开朗，通项公式也就水到渠成了。
特征值是反映变化速度的量，反映了在多个变化因素里，谁占主导地位，谁决定了变化的速度，特征向量是反映稳定性的量，决定了变化的宿命,即决定了它最终向谁收敛，所以我们看到了程序运行结果逐渐向着极限值逼近。

当编写递归程序的使用，必须满足以下几个条件

基准情形，必须有某些基准情形，在基准情形下，不用递归就能求解,如果忘记了基准情形，递归就会失控。
不断推进，对于那些需要递归求解的情形，递归调用必须朝着产生基准情形的方向前进
所有的递归调用都能运行
合成效益法则，在求解一个问题的同一个实例时，切勿在不同的递归调用中做重复性工作，这条法则说明，使用递归来计算斐波那契数列不是一个好办法，因为其中存在这很多的重复计算，以 $F(n)=F(n-1)+F(n-2)$ 为例，当计算F(n-1)时用到的 $F(n-2)$ ，后面还要重复计算一次。

递归函数中位于递归调用之前的语句，均按被调函数的顺序执行.递归函数中位于递归调用之后的语句，均按被调函数相反的顺序执行，递归过程是按照问题解决的相反顺序执行的，而回归过程则是按照解决问题的正向顺序执行的.比如下面的例子：

#include <stdio.h>

int jiecheng(int n)
{
	int res;

	printf("%s line %d, n = %d.\n", __func__, __LINE__, n);
	if (n == 1) return 1;

	res = n*jiecheng(n-1);

	printf("%s line %d, n = %d.\n", __func__, __LINE__, n);

	return res;
}

int main(void)
{
	int n = jiecheng(10);

	printf("%s line %d, n = %d.\n", __func__, __LINE__, n);
}

尾递归的特点就是回归过程没有其他函数调用，递归结果作为返回结果会者返回结果的一部分返回。

尾递归可以用循环替代实现，而一般普通递归转为非递归可以用栈实现：

#include<stdio.h>
#include<stack>
using namespace std;

struct NodeType//栈元素类型
{
	int n;//保存n值
	int f;//保存f(n)值
	int tag;//标识是否求出f(n)值，1：未求出，0：已求出 
};
int fun2(int n)
{
	NodeType e, e1, e2;
	stack<NodeType> st;
	
	e.n = n;//现在要求n的阶乘，原始n 
	e.tag = 1;//还未求出
	st.push(e);//初值进栈
	while(!st.empty())//栈不空时循环
	{
		if(st.top().tag == 1)//未计算出栈顶元素的f值
		{
			if(st.top().n == 1)
			{
				st.top().f = 1;//直接赋予阶乘值
				st.top().tag = 0;//标识已求出 
			} 
			else
			{
				e1.n = st.top().n - 1;//构建新元素e1，标识要求st.top()
				e1.tag = 1;//标识还未求出
				st.push(e1);//子任务进栈，下一次循环时处理 
			}
		}
		else //st.top().tag = 0,即已计算出栈顶元素的f值 
		{
			e2 = st.top();
			st.pop();//退栈e2
			st.top().f = st.top().n *e2.f;//根据递推式
			st.top().tag = 0; 
		} 
		if(st.size() == 1&& st.top().tag == 0) 
			break;
	}
	
	printf("%s line %d, st.size() = %ld, st.top().tag = %d, empty %d.\n",
			__func__, __LINE__, st.size(),
			st.top().tag, st.empty());
	return st.top().f; 
}

int main(void)
{
	printf("%s line %d, res %d.\n", __func__, __LINE__, fun2(6));

	return 0;
}

导致调用栈增长的，是对参数的计算，而不是函数调用，所以，尾调用天然就可以被优化掉。
递归是一种看似简单实则不易的概念，对于这个概念，不知道怎么的，总是感觉自己不知道怎么的，大脑陷入递归后容易宕机。
斐波那切数列是一种数形递归，求阶乘则是一种线性递归。树形递归效率很低，因为它做了太多冗余计算。

控制论的核心概念-反馈，不过是递归函数的一种最简单的特殊情况，不足以作为第一性原理，下图是用空控制方框图来计算递归的示意图：

迭代和递归

迭代计算的“形状”和递归不同，递归模型出现一种先逐步展开后收缩的形状，这个过程构造出一种推迟执行的运算链条，这个链条保存在堆栈里，而不是当前运算状态上下文。而迭代计算过程没有任何的增长或者收缩，对于任意一个N，在计算过程中的每一步，所有的状态都保存在当前执行的上下文里，类似于一个由固定数目的状态变量描述的计算过程，由迭代规则描述计算从一个状态到下一个状态。

迭代过程在计算过程的任意一个点，都提供了有关计算状态的完整描述，如果迭代过程被中断了也很容易通过恢复有限的几个状态得到恢复。而对于递归过程而言，还存在着不再计算上下文的
“隐含“信息，这些隐含信息并未保存在程序变量里，而是由于解释期维护，指明了在所推迟值执行的计算所形成的链条里漫游中，当前的计算过程在何处，这个链条越长，需要保存的信息也就越来多。

就实现方式来说，迭代可以利用个固定数目的寄存器实现，无需任何辅助存储器，与迭代不同，要实现递归计算过程，就需要一种机器，其中使用了堆栈。