LLM 推理优化进度大揭秘，自 DeepSeek R1 后推理时计算扩展有何新突破？

turingbooks

于 2025-04-01 17:35:28 发布

阅读量133

点赞数

文章标签：机器学习人工智能

原文链接：https://mp.weixin.qq.com/s?__biz=MjM5Njc0MjIwMA==&mid=2649833381&idx=1&sn=cebb3949634b13f9bfe0d228688ec83f&chksm=bfededefa2e36401de3223dc296a907825a9b7481d71f97b4ab4c08a34ae6aad967d29fba962&scene=126&sessionid=0

版权

提升大语言模型（LLM）的推理能力已成为 2025 年最热门的话题之一，这是有充分理由的。更强的推理能力使 LLM 能够解决更复杂的问题，在用户关心的各种任务中表现得更为出色。

在过去几周里，研究人员分享了大量提高推理能力的新策略，包括推理时计算扩展、强化学习、监督微调和模型蒸馏。许多方法结合了这些技术以达到更好的效果。

本文探讨了推理优化 LLM 的最新研究进展，特别关注自 DeepSeek R1 发布以来出现的推理时计算扩展方法。

我曾在上一篇文章「DeepSeek R1 技术揭秘：推理模型的训练与优化全流程」中解释了实现推理模型的四个主要类别。本文专注于推理时计算扩展方法。

在 LLM 中实施和改进推理：四大主要类别

由于大多数读者可能已经熟悉基于 LLM 的推理模型，这里对定义进行简短说明：基于 LLM 的推理模型是一种设计用来通过生成中间步骤或结构化的“思考”过程解决多步骤问题的 LLM。不同于仅分享最终答案的简单问答型 LLM，推理模型要么明确展示其思考过程，要么在内部处理这一过程，这使得它们在解决复杂任务如谜题、编程挑战和数学问题时表现更佳。

基础型 LLM 的一行答案与推理型 LLM 的解释性回答的并排比较

一般来说，提升推理能力主要有两种策略：增加训练计算量或增加推理计算量，这也被称为推理时扩展或测试时扩展。（推理计算指的是在训练后，为生成响应用户查询的模型输出所需的处理能力。）

准确性提升可以通过增加训练计算或测试时计算来实现，其中测试时计算与推理时计算及推理时扩展是同义的。图片来源：https://openai.com/index/learning-to-reason-with-llms/

需要注意的是，上面显示的图表让人觉得我们是通过训练时计算或测试时计算来改进推理能力的。然而，LLM 通常设计为通过结合大量的训练时计算（大量的训练或微调，通常使用强化学习或专门的数据）和增加的测试时计算（允许模型在推理过程中“思考更长时间”或执行额外的计算）来改进推理能力。

与推理时扩展同义的众多术语

为了理解推理模型是如何开发和改进的，我认为分别查看不同的技术仍然是有用的。在我之前的文章「DeepSeek R1 技术揭秘：推理模型的训练与优化全流程」中，我讨论了将其细分为四个类别的方法，如下图所示。

上图中的方法 2-4 通常会产生生成更长响应的模型，因为它们在输出中包含了中间步骤和解释。由于推理成本随着响应长度而增加（例如，响应长度翻倍则需要双倍的计算），这些训练方法本质上与推理扩展相关联。然而，在本节关于推理时计算扩展的内容中，我特别关注那些明确调节生成 token 数量的技术，无论是通过额外的采样策略、自我纠正机制还是其他方法。

本文将聚焦于自 2025年1月22日 DeepSeek R1 发布以来，有关推理时计算扩展这一有趣的新研究论文和模型发布。（最初，我打算在这篇文章中涵盖所有类别的方法，但由于篇幅过长，我决定在未来发布一篇专门讨论训练时计算方法的文章。）

在之前的文章「DeepSeek R1 技术揭秘：推理模型的训练与优化全流程」中，我讨论了 DeepSeek 推理模型的开发过程。

在我们深入探讨推理时计算扩展方法以及以推理时计算扩展类别为重点的推理模型的不同进展领域之前，让我至少提供所有不同类别的简要概述。

1. 推理时计算扩展

这一类别包括在推理时通过增加计算资源来提升模型推理能力的方法，而无需训练或修改底层模型权重。核心思想是通过增加计算资源换取更好的性能，这使得即使是固定的模型也能够通过技术手段如思维链推理和多种采样程序变得更加强大。

尽管我将推理时计算扩展单独归为一个类别，以便在这一背景下聚焦于相关方法，但需要注意的是，这项技术可以应用于任何 LLM。例如，OpenAI 使用强化学习开发了 o1 模型，并在此基础上进一步利用了推理时计算扩展。有趣的是，正如我在上一篇文章中「DeepSeek R1 技术揭秘：推理模型的训练与优化全流程」提到的，DeepSeek R1 论文明确将一些常见的推理时扩展方法（如基于过程奖励模型和基于蒙特卡洛树搜索的方法）归为“不成功的尝试”。这表明，DeepSeek 除了 R1 模型生成较长回复这一自然倾向外，并未明确采用这些技术，而这一倾向实际上是 V3 基础模型的一种隐性推理时扩展形式。然而，由于显式的推理时扩展通常是在应用层面实现的，而非 LLM 内部，DeepSeek 也承认这些技术可以轻松集成到 R1 的部署或应用中。

2. 纯强化学习

这种方法专注于仅使用强化学习（RL）来开发或提升推理能力。通常会通过数学或编码领域中可验证的奖励信号来训练模型。虽然 RL 可以让模型发展出更具战略性的思维能力和自我改进能力，但它也伴随着奖励作弊、不稳定性和高计算成本等挑战。

3. 强化学习与监督微调

这一混合方法结合了强化学习和监督微调（SFT），以实现比纯强化学习更稳定、更具泛化性的改进。通常，模型会首先使用高质量的指令数据进行 SFT 训练，然后再通过 RL 优化特定行为。

4. 监督微调与模型蒸馏

这一方法通过在高质量标注数据集上进行指令微调（SFT）来提升模型的推理能力。如果该高质量数据集由更大的 LLM 生成，这一方法通常也被称为“知识蒸馏”或直接称为“蒸馏”。需要注意的是，这与传统深度学习中的知识蒸馏略有不同，后者通常不仅使用较大教师模型的输出（标签）进行训练，还包括其 logits 信息。

推理时计算扩展方法

前一节已经简要总结了推理时计算扩展。在讨论该类别的最新研究之前，我将更详细地描述推理时计算扩展的原理。

推理时计算扩展通过在推理过程中增加计算资源（“计算量”）来提升 LLM 的推理能力。这一方法背后的思路可以用一个简单的类比来解释：人类在有更多时间思考时通常会给出更好的回答，同样地，LLM 也可以通过一些鼓励生成过程“多思考”的技术来实现性能的提升。

其中一种方法是提示工程，例如思维链（CoT）提示，提示中使用“逐步思考”等短语引导模型生成中间推理步骤。这种方式能够提升模型在复杂问题上的准确性，但对于简单的事实性查询并不必要。由于 CoT 提示会生成更多的 token，因此它会显著增加推理的计算成本。

2022 年《Large Language Models are Zero-Shot Reasoners》论文中提供了一个经典的 CoT 提示案例（https://arxiv.org/abs/2205.11916）

另一种方法是利用投票和搜索策略，比如多数投票或束搜索，通过选择最佳输出来优化生成结果。

不同的基于搜索的方法依赖于基于过程和奖励的模型来选择最优答案。图片来源：《LLM Test-Time Compute》，https://arxiv.org/abs/2408.03314）

1. S1：简单的推理时计算扩展（s1：Simple Test-Time Scaling）

本文剩余部分将重点讨论推理时计算扩展类别中，提升 LLM 推理能力的最新研究进展。我将从一篇推理时计算扩展的示例论文开始详细讨论。

该领域最近的一篇有趣的研究论文是《s1: Simple Test-Time Scaling》（2025 年 1 月 31 日），其中提出了所谓的 “wait” token，可以视为前文提到的“逐步思考”提示修改的一个更现代化版本。

需要注意的是，这种方法涉及通过 SFT 生成初始模型，因此它并不是一种纯粹的推理时计算扩展方法。然而，最终目标是通过推理时计算扩展主动控制推理行为，因此我将这篇论文归类为“1. 推理时计算扩展”类别。

简而言之，他们的方法包括两部分：

创建一个包含 1k 个训练样例的精心设计的 SFT 数据集，这些样例包括推理过程的轨迹。
通过以下方式控制生成响应的长度：
a) 添加 “Wait” token，以引导 LLM 生成更长的响应、自我验证并进行自我修正；
b) 通过添加思考结束的 token 分隔符（如 “Final Answer:”）来停止生成。他们将这种长度控制称为“预算强制（budget forcing）”。

插入 "Wait" token 控制输出长度的示例，图片来源：https://arxiv.org/abs/2501.19393

预算强制可以被看作一种顺序推理扩展技术，因为它仍然是一次生成一个 token（只是生成更多 token）。相比而言，还有像多数投票这样的并行技术，它通过聚合多个独立的生成结果来完成推理。

响应准确性与长度之间的相关性，图片来源：https://arxiv.org/abs/2501.19393

研究发现，与之前讨论的其他推理扩展技术（如多数投票）相比，他们的预算强制方法更为有效。如果要指出不足或改进之处，我希望能够看到与更复杂的并行推理扩展方法（如束搜索、前瞻搜索或 Google 在去年《Scaling LLM Test-Time Compute Optimally Can Be More Effective Than Scaling Model Parameters》论文中描述的最佳计算优化搜索方法）的对比结果。甚至可以简单对比一下经典的顺序推理方法，比如思维链提示（“逐步思考”）。

无论如何，这都是一篇非常有趣的论文和研究方法！

PS：为什么选择使用 "Wait" token？我猜研究人员可能是受到了 DeepSeek-R1 论文中 “Aha 时刻”的启发。在那项研究中，研究人员发现 LLM 会生成类似 “Wait, wait. Wait. 这是我可以在这里标记的 Aha 时刻。” 的内容，表明纯粹的强化学习可以诱导 LLM 产生推理行为。

有趣的是，他们还尝试了其他 token，比如 "Hmm"，但发现 "Wait" 的表现略胜一筹。

"Wait" 与 "Hmm" tokens 的比较。图片来源：https://arxiv.org/abs/2501.19393

其他值得关注的关于推理时计算扩展的研究论文

由于最近一个月推理模型研究领域非常活跃，为了控制文章长度，我将对其他相关论文的总结尽量简短。以下是一些与推理时计算扩展（inference-time compute scaling）相关的有趣研究文章的简要总结，按发表日期升序排列。

如前所述，并非所有这些文章都完全属于推理时计算扩展的范畴，其中一些还涉及特定的训练过程。然而，这些论文的共同点在于：控制推理时计算是其主要机制之一。（许多我将在后续文章中讨论的蒸馏或 SFT 方法也会导致更长的响应，这可以被视为一种推理时计算扩展形式。然而，这些方法并未在推理过程中主动控制响应长度，因此与这里讨论的方法有所不同。）

2. 推理时偏好优化（Test-Time Preference Optimization）

📄 2025 年 1 月 22 日，《Test-Time Preference Optimization: On-the-Fly Alignment via Iterative Textual Feedback》，详见 https://arxiv.org/abs/2501.12895

Test-Time Preference Optimization（TPO，推理时偏好优化）是一种迭代过程，可以在推理时将 LLM 的输出与人类偏好对齐，而无需改变模型的底层权重。在每次迭代中，模型会执行以下步骤：

为给定的 prompt 生成多个响应；
使用奖励模型对这些响应进行评分，并选择评分最高和最低的响应，分别作为“被选中”（chosen）和“被拒绝”（rejected）的响应；
提示模型比较并批判“被选中”与“被拒绝”的响应；
将批判内容转换为文本建议，更新模型的原始响应。

通过反复执行上述第 1-4 步，模型逐步优化其最初的响应。

图片来源：《Test-Time Preference Optimization: On-the-Fly Alignment via Iterative Textual Feedback》， https://arxiv.org/abs/2501.12895

3. 思维无处不在（Thoughts Are All Over the Place）

📄 2025 年 1 月 30 日，《Thoughts Are All Over the Place: On the Underthinking of o1-Like LLMs》，详见 https://arxiv.org/abs/2501.18585

研究者探讨了一种被称为“推理不足（underthinking）”的现象。在这种情况下，推理模型在推理过程中经常在不同的推理路径之间切换，而不是专注于探索更有前景的路径，从而降低了解决问题的准确性。

为了应对这一“推理不足”问题，他们提出了一种名为 Thought Switching Penalty（TIP，思维切换惩罚）的方法，通过调整与思维切换相关的 token 的 logits 来抑制过早切换推理路径的行为。

这一方法无需对模型进行 fine-tuning，并在多个具有挑战性的测试集上实验证明能够显著提高推理准确性。

图片来源：《Thoughts Are All Over the Place: On the Underthinking of o1-Like LLMs》，https://arxiv.org/abs/2501.18585

4. 以推理计算换取对抗鲁棒性（Trading Inference-Time Compute for Adversarial Robustness）

📄 2025 年 1 月 31 日，《Trading Inference-Time Compute for Adversarial Robustness》，详见 https://arxiv.org/abs/2501.18841

增加推理阶段的计算量（inference-time compute）在许多情况下能够提高推理类 LLM 的对抗鲁棒性（adversarial robustness），从而降低成功攻击的发生率。与对抗训练不同，这种方法无需特殊训练或对具体攻击类型的先验知识。

然而，这种方法也存在一些重要的局限性。例如，在涉及策略模糊性（policy ambiguities）或漏洞利用（loophole exploitation）的场景下，改进效果有限。此外，诸如 "Think Less" 和 "Nerd Sniping" 等新型攻击策略可能会削弱推理能力提升带来的鲁棒性增强效果。

因此，虽然研究结果表明通过扩展推理阶段的计算量可以提升 LLM 的安全性，但单靠这一方法并不能完全解决对抗鲁棒性的问题。

图片来源：《Trading Inference-Time Compute for Adversarial Robustness》， https://arxiv.org/abs/2501.18841

5. 关联思维链（Chain-of-Associated-Thoughts）

📄 2025 年 2 月 4 日，《CoAT: Chain-of-Associated-Thoughts Framework for Enhancing Large Language Models Reasoning》，详见 https://arxiv.org/abs/2502.02390

研究人员将经典的蒙特卡洛树搜索推理阶段扩展方法与“联想记忆”（associative memory）相结合，该记忆模块在推理路径探索中充当 LLM 的知识库。利用这种所谓的联想记忆，LLM 更容易回顾早期的推理路径，并在生成响应的过程中使用动态变化的信息。

图片来源：《CoAT: Chain-of-Associated-Thoughts Framework for Enhancing Large Language Models Reasoning》，https://arxiv.org/abs/2502.02390

6. 退后一步，才能更进一步（Step Back to Leap Forward）

📄 2025 年 2 月 6 日，《Step Back to Leap Forward: Self-Backtracking for Boosting Reasoning of Language Models》，详见 https://arxiv.org/abs/2502.04404

这篇论文提出了一种自回溯（self-backtracking）机制，允许 LLM 在训练和推理中学习何时以及在哪里进行回溯，从而提升推理能力。在训练阶段，模型通过 token 学会识别和纠正次优的推理路径，而论文的核心贡献在于一种推理阶段基于树的搜索方法，该方法利用学习到的回溯能力探索替代解决方案。

其独特之处在于，这种探索无需依赖外部的奖励模型（与文章“1. 推理阶段计算扩展方法”部分开头提到的基于过程奖励模型的搜索方法不同）。

图片来源：《Step Back to Leap Forward: Self-Backtracking for Boosting Reasoning of Language Models》，https://arxiv.org/abs/2502.04404

我将这篇论文列入本文，因为它非常专注于提出的回溯推理阶段扩展方法，通过动态调整搜索的深度和广度来改善推理，而不是根本性地改变训练范式（尽管需要使用 token 进行训练）。

7. 通过潜在推理扩展推理时计算（Scaling up Test-Time Compute with Latent Reasoning）

📄 2025 年 2 月 7 日，《Scaling up Test-Time Compute with Latent Reasoning: A Recurrent Depth Approach》，详见 https://arxiv.org/abs/2502.05171

研究人员并未通过生成更多 token 来提升推理能力，而是提出了一种通过在隐空间（latent space）中迭代递归深度模块（recurrent depth block）来扩展推理时计算的方法。这个模块的功能类似于 RNN 中的隐藏状态，使模型能够在无需生成更长 token 输出的情况下优化推理过程。

然而，这种方法的一个主要缺点是缺乏明确的推理步骤，而明确的推理步骤在我看来对人类可解释性非常有用，也是思维链方法的一大优势。

图片来源《Scaling up Test-Time Compute with Latent Reasoning: A Recurrent Depth Approach》， https://arxiv.org/abs/2502.05171

8. 1B LLM 能超越 405B LLM 吗？（Can a 1B LLM Surpass a 405B LLM?）

📄 2025 年 2 月 10 日，《Can 1B LLM Surpass 405B LLM? Rethinking Compute-Optimal Test-Time Scaling》，详见 https://arxiv.org/abs/2502.06703

许多推理阶段的扩展技术依赖采样，并需要一个过程奖励模型（Process Reward Model，简称 PRM）来选择最佳解答。这篇论文系统性分析了推理时计算扩展与 PRM 以及问题难度之间的关系。

研究人员提出了一种计算最优的扩展策略，该策略能够根据 PRM 的选择、策略模型以及任务复杂性进行适配。实验结果表明，采用正确的推理时计算扩展方法后，一个仅有 10 亿参数的模型可以超越没有推理阶段扩展的 4050 亿参数的 Llama 3 模型。

同样，研究还表明，7B 参数模型通过推理阶段扩展，可以超越 DeepSeek-R1，同时保持更高的推理效率。

这些发现表明，推理阶段扩展可以显著提升 LLM 的性能，甚至可以使小模型在合适的推理计算预算下超越体量更大的模型。

图片来源：《Can 1B LLM Surpass 405B LLM? Rethinking Compute-Optimal Test-Time Scaling》，https://arxiv.org/abs/2502.06703

9. 从测试时反馈中学习推理（Learning to Reason from Feedback at Test-Time）

📄 2025 年 2 月 16 日，《Learning to Reason from Feedback at Test-Time》，详见 https://www.arxiv.org/abs/2502.12521

这项研究的方法介于推理阶段方法和训练阶段方法之间，因为它会在推理阶段优化 LLM 的权重参数。

论文探索了一种方法，使得 LLM 在推理阶段可以从错误中学习，而无需将失败尝试存储到 prompt 中（这会带来高昂的成本）。与通过将先前的尝试加入上下文以精炼答案（顺序修订）或盲目生成新答案（并行采样）的常规方法不同，这种方法是在推理阶段直接更新模型的权重。

为此，作者引入了一个名为 OpTune 的小型可训练优化器，它根据模型在先前尝试中犯下的错误来更新模型权重。这意味着模型能够记住之前的错误，而不需要在 prompt 或上下文中保留错误答案。

图片来源：《Learning to Reason from Feedback at Test-Time》，https://www.arxiv.org/abs/2502.12521

10. LLM 推理与规划的推理时计算（Inference-Time Computations for LLM Reasoning and Planning）

📄 2025 年 2 月 18 日，《Inference-Time Computations for LLM Reasoning and Planning: A Benchmark and Insights》，详见 https://www.arxiv.org/abs/2502.12521

这篇论文对推理和规划任务中的多种推理阶段计算扩展技术进行了基准测试，重点分析了这些方法在计算成本与性能之间的权衡。

作者评估了多种技术，包括思维链、思维树和推理即规划，覆盖了 11 项任务，涵盖算术、逻辑、常识、算法推理和规划领域。

研究的主要发现是，尽管推理阶段计算扩展可以提升推理能力，但没有任何单一技术可以在所有任务中始终表现优越。

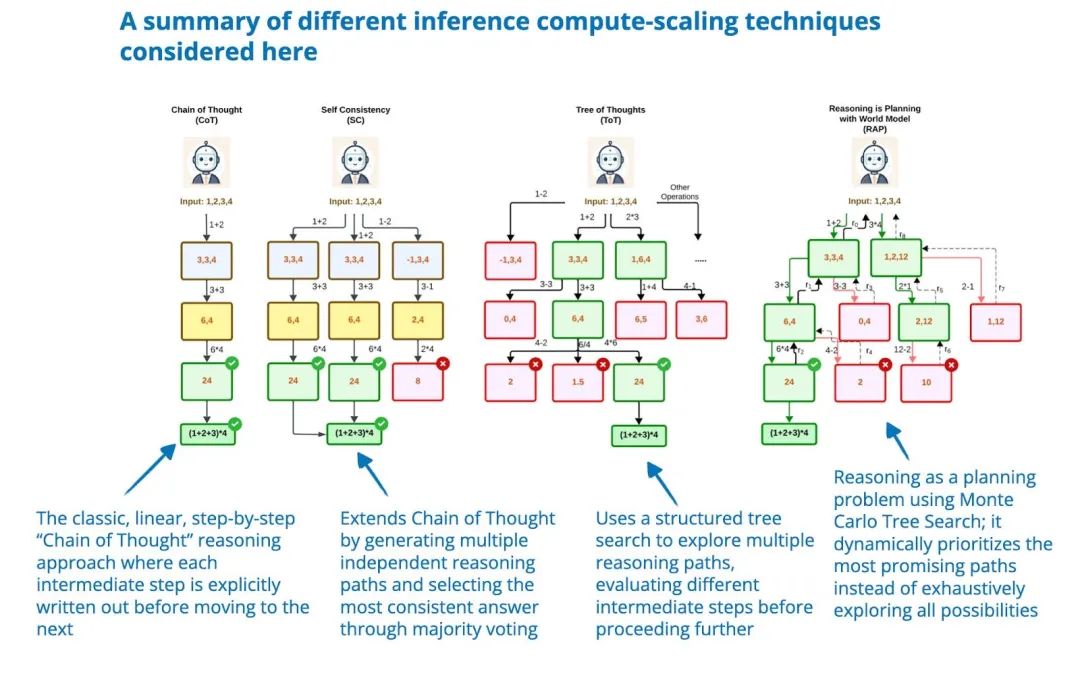图片来源：《Inference-Time Computations for LLM Reasoning and Planning: A Benchmark and Insights》，https://www.arxiv.org/abs/2502.12521

11. 内在思维 Transformer（Inner Thinking Transformer）

📄 2025 年 2 月 19 日，《Inner Thinking Transformer: Leveraging Dynamic Depth Scaling to Foster Adaptive Internal Thinking》，详见 https://arxiv.org/abs/2502.13842

Inner Thinking Transformer（ITT）能够在推理阶段动态分配更多的计算资源。不同于传统基于 Transformer 的 LLMs 对所有 token 使用固定深度（即相同的层数），ITT 采用了自适应 Token 路由（Adaptive Token Routing）机制，为困难的 token 分配更多计算资源。这些困难的 token 会多次通过相同的层进行额外处理，从而增加这些 token 的推理计算预算。

图片来源：《Inner Thinking Transformer: Leveraging Dynamic Depth Scaling to Foster Adaptive Internal Thinking》，https://arxiv.org/abs/2502.13842

12. 代码生成的推理时计算扩展（Test Time Scaling for Code Generation）

📄 2025 年 2 月 20 日，《S*: Test Time Scaling for Code Generation》，详见 https://arxiv.org/abs/2502.14382

推理时计算扩展可以通过并行扩展（生成多个答案）、顺序扩展（迭代优化答案）或两者结合的方式实现，正如 Google 在 2024 年夏季发表的论文《Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters》中所描述的那样。

S* 是一种专为代码生成设计的推理阶段计算扩展方法，它改进了并行扩展（生成多个解决方案）和顺序扩展（迭代调试）的效率。

图片来源：《S*: Test Time Scaling for Code Generation》，https://arxiv.org/abs/2502.14382

该方法分为两个阶段：

阶段 1：生成

模型生成多个代码解决方案，并使用问题提示中提供的执行结果和测试用例对它们进行迭代优化。这类似于一场编程竞赛，模型提交解决方案、运行测试并修复错误：

模型生成多个候选解决方案。
每个解决方案在公共测试用例（预定义的输入-输出对）上运行。
如果某个解决方案失败（输出错误或程序崩溃），模型会分析执行结果（错误信息、输出）并修改代码以改进它。
这一优化过程会不断迭代，直到模型找到通过测试用例的解决方案。

例如，假设模型被要求实现一个函数 is_even(n)，该函数用于判断一个数是否为偶数，如果是返回 True，否则返回 False。

模型的第一次尝试可能是：

def is_even(n):
    return n % 2  # ❌ Incorrect: should be `== 0`

模型使用公共测试用例对该实现进行测试：

Input         Expected Model Output Status
is_even(4) True         False         ❌ Fail
is_even(3) False         True         ❌ Fail

在查看结果后，模型发现 4 % 2返回的是 0而不是 True，因此修改了函数：

def is_even(n):
    return n % 2 == 0  # ✅ Corrected

现在该函数通过了所有的公共测试用例，完成了调试阶段。

阶段 2：选择

当多个解决方案通过公共测试用例后，模型需要选择最优解（如果可能）。此时，S* 引入了自适应输入生成（adaptive input synthesis）机制以避免随机选择：

模型比较两个都通过了公共测试的解决方案。
模型自问：“我能生成一个输入来区分这两个解决方案吗？”
模型生成一个新的测试输入并运行两个解决方案。
如果一个解决方案生成了正确的输出而另一个失败，模型会选择更好的那个。
如果两个解决方案的行为完全一致，模型会随机选择一个。

例如，考虑两种不同实现的 is_perfect_square(n)函数：

import math

def is_perfect_square_A(n):
    return math.isqrt(n) ** 2 == n

def is_perfect_square_B(n):
    return math.sqrt(n).is_integer()

它们在简单测试用例上都通过了测试：

n = 25
print(is_perfect_square_A(n))  # ✅ True (Correct)
print(is_perfect_square_B(n))  # ✅ True (Correct)

但当 LLM 生成边界情况时，可以看到其中一个失败，因此模型会选择解决方案 A。

n = 10**16 + 1
print(is_perfect_square_A(n))  # ✅ False (Correct)
print(is_perfect_square_B(n))  # ❌ True (Incorrect)

13. 草稿链（Chain of Draft）

📄 2025 年 2 月 25 日，《Chain of Draft: Thinking Faster by Writing Less》，详见 https://arxiv.org/abs/2502.18600

研究者观察到，尽管推理 LLM 通常会生成详细的逐步解释，但人类往往依赖于简洁的草稿，仅记录必要的信息。

受到这一现象的启发，他们提出了 Chain of Draft（CoD），这是一种通过生成最简明但具有信息量的中间步骤来减少冗长表达的提示策略。某种意义上，它是一种推理阶段的扩展方法，通过生成更少的 token 提高推理阶段的效率。

图片来源：《Chain of Draft: Thinking Faster by Writing Less》， https://arxiv.org/abs/2502.18600

从实验结果来看，CoD 的表达简洁程度几乎接近标准提示方法（standard prompting），但准确性却与 Chain of Thought（CoT）提示相当。正如我之前提到的，在我看来，推理模型的一个优势是用户可以通过阅读推理过程来学习并更好地评估/信任模型的回答。而 CoD 在一定程度上削弱了这种优势。然而，在某些场景下，如果不需要详细的中间步骤，CoD 会非常有用，因为它在保持 CoT 准确性的同时显著提升了生成速度。

14. 更好的反馈与编辑模型

📄 2025 年 3 月 6 日，《Dedicated Feedback and Edit Models Empower Inference-Time Scaling for Open-Ended General-Domain Tasks》，详见 https://arxiv.org/abs/2503.04378

许多推理阶段扩展技术依赖于具有可验证答案的任务（例如可以检查的数学和代码），因此难以应用于开放性任务，如写作和通用问题求解。

为了解决可验证答案的局限性，研究者提出了一种新系统，其中一个模型负责生成初始回答，另一个模型提供反馈（“feedback model”），第三个模型基于反馈优化回答（“edit model”）。

他们利用包含大量人类标注回答与反馈的数据集训练这些专门的“反馈模型”和“编辑模型”。在推理阶段，这些模型通过生成更优质的反馈并进行更高效的编辑，来改进模型的回答质量。

结论

推理时计算扩展已经成为今年提升大语言模型推理能力的热门研究课题之一，这种方法无需修改模型权重即可实现性能提升。

我在上文中总结的众多技术涵盖了从简单的基于 token 的干预（例如 “Wait” tokens）到更复杂的基于搜索和优化的策略（例如 Test-Time Preference Optimization 和 Chain-of-Associated-Thoughts）。

从宏观角度来看，一个反复出现的主题是，通过在推理阶段增加计算量，即使是相对较小的模型也能在推理基准测试中相比标准方法实现显著提升。

这表明推理策略可以帮助缩小小型、更具成本效益的模型与大型模型之间的性能差距。

成本权衡

需要注意的是，推理时计算扩展会增加推理成本，因此，选择是使用一个小型模型并进行大规模推理扩展，还是训练一个更大的模型并减少或不进行推理扩展，需要根据模型的实际使用频率来计算权衡。

例如，一个采用了重度推理阶段扩展的 o1 模型，实际上仍然比一个更大的 GPT-4.5 模型（可能不使用推理阶段扩展）略便宜。

（看 GPT-4.5 在使用 o1 或 o3 风格的推理阶段计算扩展时表现如何将会很有趣。）

哪种技术？

不过，推理时计算扩展并不是万能的。虽然像蒙特卡洛树搜索、自回溯（self-backtracking）和动态深度扩展（dynamic-depth scaling）等方法可以显著提升推理性能，但其效果仍然取决于任务类型和难度。正如早期的一些论文所显示的，目前没有哪种推理时计算扩展技术能在所有任务中都表现最佳。

此外，许多方法通过牺牲响应速度来换取更强的推理能力，而较慢的响应速度可能会让一些用户感到不耐烦。例如，当我处理简单任务时，我通常会从 o1 切换到 GPT4o，因为它响应更快。

下一步

展望未来，我认为今年将会有更多围绕“通过推理时计算扩展实现推理能力”的两大研究方向的论文出现：

专注于开发能在基准测试中达到最佳表现的模型的研究。
专注于平衡推理任务中成本与性能权衡的研究。

无论如何，推理时计算扩展的优势在于，它可以应用于任何现有的大语言模型，并针对特定任务进行优化提升。

按需思考

在工业界，一个有趣的趋势是我称之为“按需思考”。自 DeepSeek R1 发布以来，许多公司似乎都在争相为自己的产品添加推理能力。

一个有趣的现象是，目前大多数 LLM 提供商都增加了用户可以启用或禁用推理功能的选项。虽然相关机制尚未公开，但很可能是通过对同一个模型调整推理阶段计算扩展的强度实现的。例如，Claude 3.7 Sonnet 和 Grok 3 都新增了一个“思考”功能，用户可以自行启用，而 OpenAI 则要求用户在不同模型之间切换。例如，用户需在 GPT 4o/4.5 和 o1/o3-mini 模型之间选择，才能使用明确的推理模型。不过，OpenAI 的 CEO 表示，GPT 4.5 可能会是他们最后一款没有明确区分推理模式或“思考模式”的模型。在开源领域，甚至连 IBM 都为其 Granite 模型新增了一个明确的“思考”切换功能。

总体而言，无论是通过推理阶段还是训练阶段的计算扩展来添加推理能力，这都是 2025 年 LLM 发展的一大进步。

随着时间推移，我预计推理能力将不再被视为一种可选或特殊功能，而是会像如今的指令微调模型或基于 RLHF 微调的模型一样，成为标准配置，而不是单纯的预训练模型。

正如前文提到的，由于推理阶段计算扩展的研究已经非常活跃，我在本文中仅集中讨论了推理阶段计算扩展的相关内容。在未来的文章中，我计划涵盖所有与推理能力相关的训练阶段计算扩展方法。

我的新书《从零构建大模型》电子版已经上市，欢迎大家购买支持！纸质书预计下周上市！可以根据自身需求购买！