常用的概率分布:二项式分布，贝塔分布，狄里克雷分布

知识点：伯努利分布、二项式分布、多项式分布、先验概率，后验概率，共轭分布、贝塔分布、贝塔-二项分布、负二项分布、狄里克雷分布，伽马函数、分布

一，伯努利分布(bernouli distribution)

---

又叫做0-1分布，指一次随机试验，结果只有两种。也就是一个随机变量的取值只有0和1。
记为：0-1分布 或 $B(1,p)$，其中$p$表示一次伯努利实验中结果为正或为1的概率。
概率计算：

$$P(X=0) = p_0$$

$$P(X=1) = p_1$$
期望计算： $$E(X) = 0*p_0 + 1*p_1 = p_1$$
最简单的例子就是，抛一次硬币，预测结果为正还是反。

二，二项式分布(binomial distrubution)

---

表示n次伯努利实验的结果。
记为：$X\sim B（n,p）$，其中n表示实验次数，p表示每次伯努利实验的结果为1的概率，X表示n次实验中成功的次数。
概率计算：

$$P(X=k) = C_n^k p^k (1-p)^{n-k}, k=0,1,2,...,n$$
期望计算： $$E(X) = n*p$$
例子就是，求多次抛硬币，预测结果为正面的次数。

三，多项式分布(multinomial distribution)

---

多项式分布是二项式分布的扩展，不同的是多项式分布中，每次实验有n种结果。
概率计算：

$$P(X_1 = n_1,...,X_k=n_k)=\left\{ \begin{matrix} n!\prod_{i=1}^k \frac{p_i^{n_i}}{n_i!}, \sum_{i=1}^kn_i=n \\0, otherwise \end{matrix} \right.$$ 期望计算： $$E(X_i) = n*p_i$$
最简单的例子就是多次抛筛子，统计各个面被掷中的次数。

四，先验概率，后验概率，共轭分布

---

先验概率和后验概率 ：

先验概率和后验概率的概念是相对的，后验的概率通常是在先验概率的基础上加入新的信息后得到的概率，所以也通常称为条件概率。比如抽奖活动，5个球中有2个球有奖，现在有五个人去抽，小名排在第三个，问题小明抽到奖的概率是多少？初始时什么都不知道，当然小明抽到奖的概率$P(X=1)=\frac{2}{5}$。但当知道第一个人抽到奖后，小明抽到奖的概率就要发生变化，$P(X=1|Y_1=1)=\frac{1}{4}$。再比如自然语言处理中的语言模型，需要计算一个单词被语言模型产生的概率$P(w)$。当没有看到任何语料库的时候，我们只能猜测或者平经验，或者根据一个文档中单词w的占比，来决定单词的先验概率$P(w)=\frac{1}{1000}$。之后根据获得的文档越多，我们可以不断的更新$P(w)=\frac{count(w)_{old}+count(w)_{new}}{|D_{old}|+|D_{new}|}$。也可以写成$P(w|D_{new})=\frac{count(w)_{old}+count(w)_{new}}{|D_{old}|+|D_{new}|}$。再比如，你去抓娃娃机，没抓之前，你也可以估计抓到的概率，大致在$\frac{1}{5}$到$\frac{1}{50}$之间，它不可能是$\frac{1}{1000}$或$\frac{1}{2}$。然后你可以通过投币，多次使用娃娃机，更据经验来修正，你对娃娃机抓到娃娃的概率推断。后验概率有时候也可以认为是不断学习修正得到的更精确，或者更符合当前情况下的概率。

共轭分布 ：

通常我们可以假设先验概率符合某种规律或者分布，然后根据增加的信息，我们同样可以得到后验概率的计算公式或者分布。如果先验概率和后验概率的符合相同的分布，那么这种分布叫做共轭分布。共轭分布的好处是可以清晰明了的看到，新增加的信息对分布参数的影响，也即概率分布的变化规律。
这里有个疑问是，如何由先验分布得到后验分布，如何选择？下面举例beta分布进行详解。

$p(\theta |X)=p(X|\theta)p(\theta)$，通常我们称$p(\theta |X)$为后验概率，即添加观测$X$后的概率。$p(X|\theta)$为似然函数，为模型。$p(\theta)$为先验概率。通常$p(X|\theta)$修正求解的模型，$\theta$为模型的参数。参数$\theta$不是一个固定的值，也是服从某种分布$p(\theta)$。我们可以通过贝叶斯后验公式来更新$\theta$。如果$\theta$的先验概率$p(\theta)$和后验概率$p(\theta |X)$是同一种分布，那么似然函数$p(X|\theta)$和先验概率$p(\theta)$共轭，因为求出来后验概率和先验概率是同一种分布。

五，贝塔分布(beta distribution)

计算公式：

$$P(x) = Beta(x;\alpha,\beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0^1 \mu^{\alpha-1}(1-\mu)^{\beta-1}d\mu} =\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1} =\frac{1}{B(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1} ，$$ 其中，B(a,b)是beta函数。
期望： $$E(p) = \frac{a}{a+b}$$
首先，现实生活中我们通常需要估计一件事情发生的概率，如抛一次硬币为正面的概率。我们可以进行统计的方式给出答案，比如抛了100次硬币，其中有30次向上，我们就可以说这个硬币为正面的概率是0.3。当然我们可以从另外一个角度回答问题，比我对实验的公信度进行怀疑，我就可以说为正面的概率是0.3的可能性是0.5，为0.2的可能性是0.2，为0.4的概率是0.3，给出硬币为正面的概率的分布，即伯努利实验中p的分布。给出参数的分布，而不是固定值，的好处有很多。

• 一，如抛100次中，30次向上，和抛100000次中30000次向上，两者估计p的值都是0.3。但后者更有说服力。如果前者实验得到p为0.3的置信度是0.5的话，后者实验得到p为0.3的置信度就有可能是0.9，更让人信服。
• 二，估计一个棒球运动员的击球命中率。如果我们统计一个新棒球运动员的比赛次数，发现，3场比赛中，他击中2次，那么我们可以说他的击球命中率是$\frac{2}{3}$么？显然不合理，因为因为根据棒球的历史信息，我们知道这个击球率应该是0.215到0.36之间才对。但如果我们给出的是击球明中率的分布，而不是固定的值，就可以表示我们对当前击球命中率估计的置信度，提供了更加丰富的信息。因为只观察了三次比赛，所以我们得到运动员命中率为$\frac{2}{3}$的概率是0.1，表示我们对这个命中率值不确定。

接着进入正题：由前面可知，我们的需求是为了模拟模型参数的模型，beta分布是来模拟”取值范围是从0到1时的模型的参数的分布”。比如就求抛硬币为正的概率p为例。如果我们知道p的取值，我们就可以计算抛10次硬币，其中有1次向上的概率是$P(X=1)=C_n^1 p(1-p)^9$，有3次向上的概率是$P(X=1)=C_n^3 p^3(1-p)^7$，有6次向上的概率是$P(X=6)=C_n^6 p^3 (1-p)^7$。那么我们如何求p值呢？
前面说的有两种方法，一个是给固定的值 ，一个给值的密度分布函数。我们这里介绍后者，假设p值符合Beta分布。即$P(p)=Beta(p;a,b)= \frac{p^{a-1}(1-p)^{b-1}}{B(a,b)}$。那么现在我们又做了10次实验，其中4次为正，6次为反，称为信息X。那么我们现在要计算得到信息X后概率p的分布，即P(p|X)，根据贝叶斯条件概率计算公式

$$P(p|X)=\frac{P(X|p)*P(p)}{P(X)}$$ $$=\frac{P(X|p)*P(p)}{\int_0^1 P(X|p_i)*P(p_i) dp_i}$$ $$=\frac{\left(C_{10}^4 p^4(1-p)^6\right) *\left (\frac{p^{a-1}(1-p)^{b-1}}{B(a,b)} \right)}{\int_0^1 \left(C_{10}^4 p_i^4(1-p_i)^6\right) * \left(\frac{p_i^{a-1}(1-p_i)^{b-1}}{B(a,b)} \right) dp_i}$$ $$=\frac{(p^4(1-p)^6) * (p^{a-1}(1-p)^{b-1})}{\int_0^1 (p_i^4(1-p_i)^6) * (p_i^{a-1}(1-p_i)^{b-1}) dp_i}$$ $$=\frac{p^{4+a-1}(1-p)^{6+b-1}}{\int_0^1 p_i^{4+a-1}(1-p_i)^{6+b-1} dp_i}$$ $$=\frac{p^{4+a-1}(1-p)^{6+b-1}}{B(4+a,6+b)}$$ $$=Beta(p;4+a,6+b)$$ ，这里使用最大似然估计计算P(X|p)，即 $P(X|p)=C_{10}^4 p^4(1-p)^6$， $P(p)$和 $P(p_i)$使用的是先验概率（贝叶斯概率本来就是用先验概率计算后验概率的公式）。其中分子分母中 $C_{10}^4$和 $B(a,b)$函数是常数项可以约去，最后得到： $P(p|X)=Beta(p,a+4,b+6) ,p\in [0,1]$。
重新解释下整个过程，目的是计算得到p的概率分布，而不是固定的值。首先根据之前的经验或者统计，假设p服从Beta(a,b)分布，a表示之前统计中为正的次数，b为之前统计中为负的次数。接着，根据新做的实验或者新到达的信息X，来修正p的分布，修正后的p同样是服从Beta分布，只不过是参数由(a,b)变成(a+m,b+n)，m表示新得到的信息中为正的次数，n表示新得到的信息中为负的次数。这样的修正过程可以很直观的被理解，而且修改前后是兼容的，很好的体现了一个学习修正的过程。

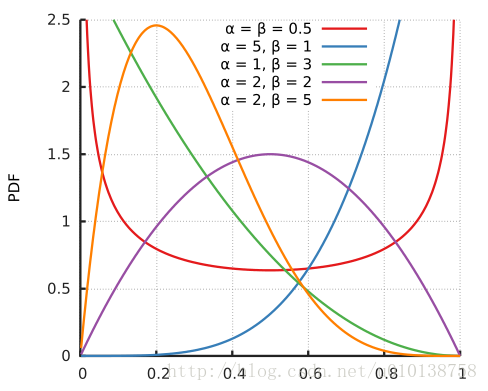
贝塔分布的pdf图：

六，贝塔-二项分布(beta-binomial distribution)

The beta-binomial distribution is the binomial distribution in which the probability of success at each trial is not fixed but random and follows the beta distribution.
贝塔-二项分布是指，二项分布中的参数p不是固定的值，是服从Beta(a,b)分布。
计算公式:

$$P(X=k|p,n)=L(p|k)=C_n^k p^k(1-p)^{n-k}$$ 其中 $L(p|k)$表示二项式分布的最大似然估计计算方式。然后将 $\pi(p|a,b)=Beta(a,b)$整合到p得， $$P(X=k|p,n)=\int_0^1 L(p|k) \pi(p|a,b)dp$$ $$= \frac{C_n^k}{B(a,b)} \int_0^1 p^{k+a-1}(1-p)^{n-k+b-1}dp$$ $$= \frac{C_n^k * B(k+a,n-k+b)}{B(a,b)}$$ 期望： $$E(X)=\frac{na}{(a+b)}$$

七，负二项分布(negative binomial distribution)

Suppose there is a sequence of independent Bernoulli trials. Thus, each trial has two potential outcomes called “success” and “failure”. In each trial the probability of success is p and of failure is (1 − p). We are observing this sequence until a predefined number r of failures has occurred. Then the random number of successes we have seen, X, will have the negative binomial (or Pascal) distribution。
一次伯努利实验分为成功和失败两个结果。现在观察连续伯努利实验，直到r次失败事件产生为止，我们观察到成功的个数。记为：$X\sim NB(r,p)$。比如我们可以用来模拟机器在出故障前可以工作的天数的分布，即一个新机器可以运行多少天不出故障。
计算公式：

$$f(k;r,p)=P_r(X=k)=C_{k+r-1}^kp^k(1-p)^r=C_{k+r-1}^{r-1}p^k(1-p)^r, k=0,1,2...。$$ (注意：是k+r-1个种选取k个，不是k+r，因为最后一个是固定的1-p。)
期望：
$E(N)=\frac{r}{(1-p)}$,N表示要想观察到r次失败，需要进行试验的总次数。
$E(K)=N-r=\frac{r}{(1-p)} - r =\frac{rp}{(1-p)}$，相当于成功和失败的比例是 $\frac{K}{r}=\frac{p}{1-p}$。

八.零，伽马函数，伽马分布(gamma distribution)，贝塔函数

伽马函数：

$$\Gamma(n)=(n-1)!，n是正整数\\ \Gamma(z)=\int_0^{\infty}x^{z-1}e^{-x}dx，z是复数，但不包括0和负整数$$
下图是伽马函数在复数域和实数域上的图像：

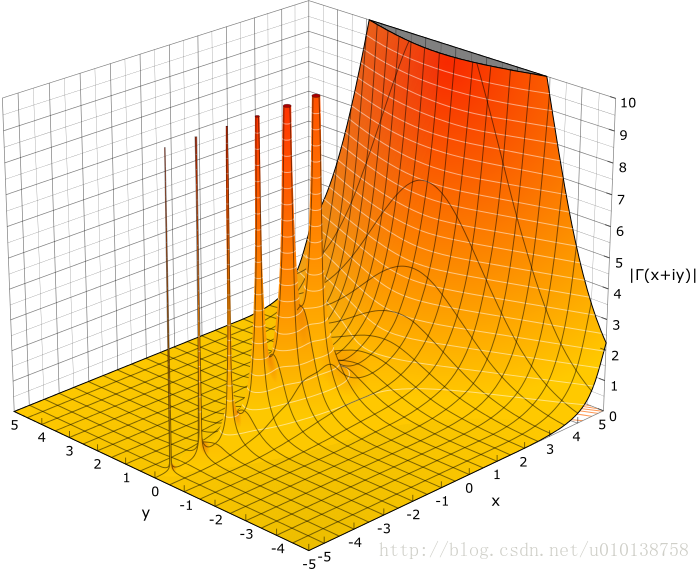
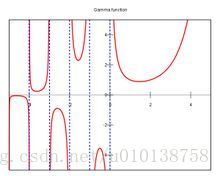
有了伽马函数我们就可以计算$2.5!$和$0.3!$和$(1.1+2.4i)!$。
贝塔函数：
贝塔函数是01区间上的积分：

$$B(x,y)=\int_0^1t^{x-1}(1-t)^{y-1}dt=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$$
在狄里克雷中我们定义：
$$B(\alpha)=\frac{\prod_{k=1}^K \Gamma(\alpha_k)}{\Gamma(\sum_{k=1}^K \alpha_k )} ，分子是伽马函数的乘积，分母是和的伽马函数$$

---

从统计学或者概率论角度来说，指数分布，正态分布，泊松分布，卡方分布，均匀分布等等，其根源（我是指数学根源，而非实际问题根源），都是来自于这两个函数。

---

伽马分布：

$$f(x;\alpha \beta)=\frac{\beta^{\alpha}x^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)} \\ \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt \\ 若令t=\beta x,则 \Gamma(\alpha,\beta)=\beta^{\alpha} \int_0^\infty x^{\alpha-1}e^{-x\beta}dx$$

假设随机变量X为等到第α件事发生所需之等候时间。（不是很理解，之后在学习吧）

怎么来理解伽玛（gamma）分布？ - T Yuan的回答 - 知乎
https://www.zhihu.com/question/34866983/answer/60541847

八，狄里克雷分布(Dirichlet distribution)

由前面的介绍可以知道，当前后验概率相同共轭时，有两个关键的部分，即Beta分布的推导过程中，先是参数个数是一个，p，而且求P(X|p)是采用二项分布的计算公式。现在进行推广，将参数有1个推广到多个，求P(X|p*)采用多项式分布的计算公式。
计算公式：

$$p(\pi|\alpha)=\frac{\Gamma(\sum_{k=1}^K \alpha_k )}{\prod_{k=1}^K \Gamma(\alpha_k)} \prod_{k=1}^K \pi_k^{\alpha_k-1}$$ 期望： $$E(\pi_k) = \frac{\alpha_k}{(\alpha_1+\alpha_2+...+\alpha_K)}$$
简单举例，beta分布是模型抛硬币为正的 概率的分布，Dirichlet可以是掷骰子模型中的 参数的分布。刚刚开始假设筛子个个面被掷中概率服从 $Dirichlet(\pi|10,10,20,20,20,20))$。现在又做了100次掷骰子实验，假设为1的次数是20，为2的次数是10，为3的次数是40，为4的次数是10，为5的次数是10，为6的次数是10。所以根据贝叶斯后验概率公式和多项式分布更新得到筛子个个面被掷中概率服从 $Dirichlet(\pi|(30,20,60,30,30,30))$。

贝塔分布和狄里克雷分布一般都作为参数的分布。
贝塔分布可以写成：
$P(x_1,x_2) =Beta(x_1,x_2;\alpha,\beta)=\frac{x_1^{\alpha-1}x_2^{\beta-1}}{\int_0^1 \mu^{\alpha-1}(1-\mu)^{\beta-1}d\mu}$，
其中$x_1+x_2=1$。公式很容易记住，上面就是每个x与其对应的参数减一的指数，相乘，然后分母就是01区间上积分，相当于归一化处理。
狄里克雷分布也同样写成：
$p(\pi_1,\pi_2,...,\pi_K|\alpha)=\frac{\Gamma(\sum_{k=1}^K \alpha_k )}{\prod_{k=1}^K \Gamma(\alpha_k)} \prod_{k=1}^K \pi_k^{\alpha_k-1}=\frac{\prod_{k=1}^K \pi_k^{\alpha_k-1}}{B(\alpha_1,\alpha_2,...\alpha_K)}$。
其中$\pi_1+\pi_2+...+\pi_K=1$。和贝塔分布一样，分子是每个x与其对应的参数减一的指数，相乘，然后分母就是01区间上积分，相当于归一化处理。

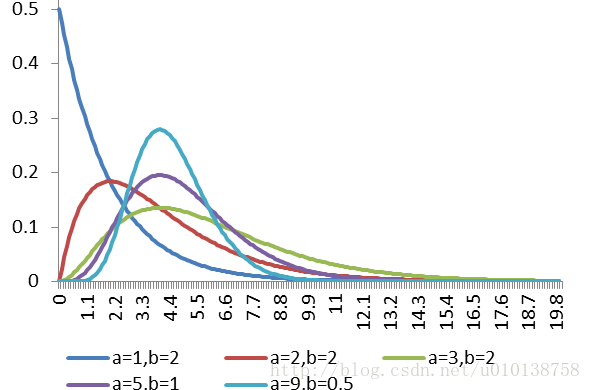
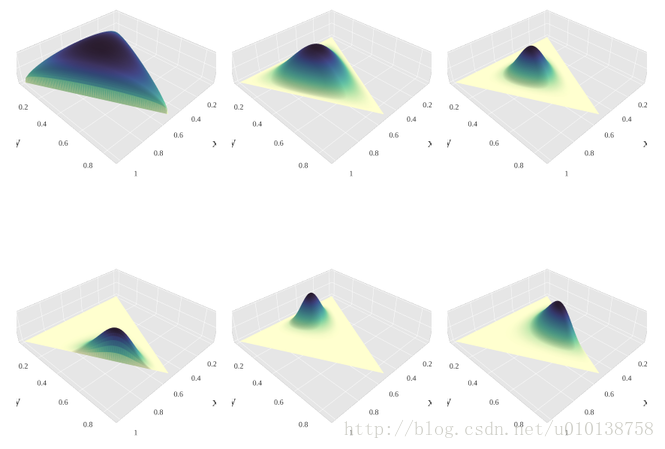
狄里克雷的pdf图：

九，几何分布（Geometric distribution）

几何分布（Geometric distribution）是离散型概率分布。其中一种定义为：在n次伯努利试验中，试验k次才得到第一次成功的机率。或者定义为：在n次伯努利试验中，需要失败k次才得到第一次成功的机率。两者的区别在于前者k取值从1到无穷，后者k取值从0到无穷。（后面的公式以第一种定义为例）
根据定义显然几何分布表示前k-1次试验都失败，只要最后第k次试验成功即可。
计算公式：

$$p(X=k)=(1-p)^{k-1}p$$ 期望： $$E(X) = \frac{1}{p}$$ 方差： $$VAR(X) = \frac{1-p}{p^2}$$

参考：

https://www.zhihu.com/question/23749913?f=41824312

http://nooverfit.com/wp/%E7%94%A8python%E5%81%9A%E8%B4%9D%E5%8F%B6%E6%96%AFab%E6%B5%8B%E8%AF%95-%E8%B4%9D%E5%8F%B6%E6%96%AFab%E6%B5%8B%E8%AF%95%E5%85%A5%E9%97%A8-%E4%BB%A5%E5%8F%8A%E5%85%B1%E8%BD%AD/

https://www.zhihu.com/question/41846423

https://www.zhihu.com/question/39004744

https://www.zhihu.com/question/30269898

https://en.wikipedia.org/wiki/Beta-binomial_distribution

https://en.wikipedia.org/wiki/Negative_binomial_distribution