漫步线性代数十四——正交和子空间

基是无关向量的集合，他们可以生成一个空间。几何上，它是坐标轴的集合，没有这些坐标轴也可以定义向量空间，但是每次我们考虑$x-y$平面和三维空间空间或$R^n$时，就会用到坐标轴，他们通常是互相垂直的！在选择基的时候，我们倾向于选择一个正交基。

正交基的想法是线性代数基本内容之一，我们需要一个基将几何转变为代数计算，而正交基可以让计算更加容易，再特殊一点：向量长度为1。对于一个正交基(正交单位向量)，我们将找到

• 向量的长度$\parallel x\parallel$;
• 用$x^Ty=0$来测试是否是正交向量；
• 如何从线性无关向量中构建垂直向量

不仅向量是垂直的，子空间也可以是垂直的。我们会看到基本子空间旋转90度将会相遇，这四个子空间有两对是垂直的，一对在$R^m$中，一对在$R^n$中，这些内容将填补线性代数的基本定理。

第一步是找出向量的长度，我们用$\parallel x\parallel$来表示，在二维空间中它是直角三角形的斜边(图1a)，长度的平方根据毕达哥拉斯定理得到：$\parallel x\parallel^2=x_1^2+x_2^2$。

图1

在三维空间里，$x=(x_1,x_2,x_3)$是盒子的对角线(图1b)，两次应用毕达哥拉斯定理就能求出它的长度。首先是底面二维平面上$(x_1,x_2,0)=(01,2,0)$，它和垂直边$(0,0,x_3)=(0,0,3)$夹角是直角，再次利用毕达哥拉斯得出斜边$\parallel x\parallel$的长度：

$$\parallel x\parallel^2=1^2+2^2+3^2\quad \parallel x\parallel=\sqrt{x_1^2+x_2^2+x_3^2}$$

由此可以立刻扩展到$n$为空间，利用毕达哥拉斯$n-1$次，$R^n$中的长度$\parallel x\parallel$是$x^Tx$正的平方根：

$$\begin{equation} \parallel x\parallel^2=x_1^2+x_2^2+\cdots+x_n^2=x^Tx\tag1 \end{equation}$$

这个平方和等于$x^Tx$，$x=(1,2,-3)$的长度是$\sqrt{14}$：

$$x^Tx=\begin{bmatrix}1&2&-3\end{bmatrix} \begin{bmatrix} 1\\2\\-3 \end{bmatrix} =1^2+2^2+(-3)^2=14$$

正交向量

我们如何判断两个向量$x,y$是否正交呢？图2中正交测试是什么？在平面中旋转$x,y$，这些向量夹角为直角，所以正交，考虑$a^2+b^2=c^2$：

$$\begin{equation} \parallel x\parallel^2+\parallel y\parallel^2=\parallel x-y\parallel^2\tag2 \end{equation}$$

利用长度公式(1)，$R^n$的正交测试变为

$$(x_1^2+\cdots+x_n^2)+(y_1^2+\cdots+y_n^2)=(x_1-y_1)^2+\cdots+(x_n-y_n)^2$$

右边的每一项$(x_i-y_i)^2$多处一个$-2x_iy_i$：

$$\text{右边}=(x_1^2+\cdots+x_n^2)-2(x_1y_1+\cdots+x_ny_n)+(y_1^2+\cdots+y_n^2)$$

当$x_iy_i$的和为零时，三角形才是直角的：

$$\begin{equation} x^Ty=x_1y_1+\cdots+x_ny_n=0\tag3 \end{equation}$$

和$x^Ty=\Sigma x_iy_i=y^Tx$表示行向量$x^T$和列向量的乘积：

$$\begin{equation} x^Ty=\begin{bmatrix} x_1&\cdots&x_n \end{bmatrix} \begin{bmatrix} y_1\\\vdots\\y_n \end{bmatrix} =x_1y_1+\cdots+x_ny_n\tag4 \end{equation}$$

这个数也叫作标量乘法或点乘，用$(x,y)$或$x\cdot y$表示，以后我们统一使用内积，并且使用符号$x^Ty$。

1、当且仅当$x,y$是正交向量时，他们的内积$x^Ty$ 是零。如果$x^Ty>0$，那么他们的角度小于90度；如果$x^Ty<0$，那么他们的角度大于90度。

$x$长度的平方等于它和自身的内积：$x^Tx=x_1^2+\cdots+x_n^2=\parallel x\parallel ^2$，长度为零的向量是零向量，它是唯一一个自己跟自己垂直的向量，并且向量$x=0$和$R^n$中的所有向量都垂直。

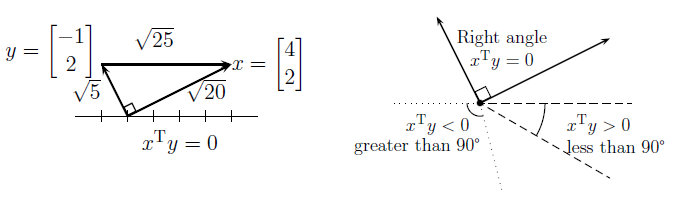
图2

例1：$(2,2,-1)$和$(-1,2,2)$正交，长度都为$\sqrt{4+4+1}=3$。

有用的事实：如果非零向量$v_1,\cdots,v_k$互相正交(每个向量和其他所有向量垂直)，那么这些向量是线性无关的。

证明：假设$c_1v_1+\cdots+c_kv_k=0$，为了说明$c_1$必须为零，我们用$v_1$和两边进行内积，根据正交性只留下了一项：

$$\begin{equation} v_1^T(c_1v_1+\cdots+c_kv_k)=c_1v_1^Tv_1=0\tag5 \end{equation}$$

这些向量都是非零的，所以$v_1^Tv_1\neq 0$，从而$c_1=0$。我们用每个$c_i$进行同样的操作得到相同的事实，$v$得到零的唯一组合就是$c_i=0$：无关！

$R^n$中的坐标向量$e_1,\ldots,e_n$是最重要的正交向量，他们是单位矩阵的列，是$R^n$最简单的基，并且还是单位向量——每个长度为$\parallel e_i\parallel=1$。他们都沿着坐标轴，如果坐标轴旋转，那就就产生新的基：一个新的互相正交单位向量系统，在$R^2$中我们有$\cos^2\theta+\sin^2\theta=1$：

$$v_1=(\cos\theta,\sin\theta),\quad v_2=(-\sin\theta,\cos\theta)$$

正交子空间

我们现在处理两个子空间的正交性。一个子空间的每个向量与另一个空间的每个向量都正交时，这两个子空间才是正交的。$R^3$子空间的维数可以是0,1,2或者3，这些子空间可以用通过原点的直线或平面表示——极端的情况就是只有原点或整个空间。子空间${0}$和其他所有子空间都是正交的，一条直线可以和另一条直线正交，或者和一个平面正交，但是平面不可能和一个平面正交。

考虑一间屋子，竖直的墙面和地板所在的平面看着就是垂直的啊，但是根据我们的定义，他们不是垂直的！我们在竖直墙面上随便做出两条线$v,w$，他们和两个面的交线夹角就不是直角。

2、对于$R^n$空间中的两个子空间$V,W$，如果$V$中的每个向量和$W$中的每个向量是正交的：$v^Tw=0$，那么子空间是正交的。

例2：假设$V$是由$v_1=(1,0,0,0)$ 和$v_2=(1,1,0,0)$生成的平面，如果$W$是$w=(0,0,4,5)$生成的直线，那么$w$和所有的$v$是正交的，线空间$W$将和整个平面$V$正交。

这种情况下，$R^4$的两个子空间维数为2和1，还有空间来容纳第三个子空间。通过$z=(0,0,5,-4)$的直线$L$垂直于$V,W$，那么维数加起来是$2+1+1=4$。现在有个疑问，什么空间对$V,W,L$ 都垂直呢？

正交子空间不是偶然就出现了，他们两个是同时出现的。事实上正交子空间肯定存在：他们是基本的子空间！第一对是零空间和行空间。他们是$R^n$的子空间——行有$n$个元素并且$Ax=0$中的$x$也有$n$个元素。接下来我们就来说明$A$的行和零空间中的向量$x$是正交的。

3、正交的基本定理：行空间和零空间($R^n$)是正交的；列空间和左零空间($R^m$)是正交的。

证明1：假设$x$是零空间中的向量，那么$Ax=0$，$m$个方程的系统可以写成$A$的行乘以$x$：

$$\begin{equation} Ax=\begin{bmatrix} \cdots&row\ 1&\cdots\\\cdots&row\ 2&\cdots\\\vdots&\vdots&\vdots\\\cdots&row\ m&\cdots \end{bmatrix} \begin{bmatrix} x_1\\x_2\\\vdots\\x_n \end{bmatrix}= \begin{bmatrix} 0\\0\\\vdots\\0 \end{bmatrix}\tag6 \end{equation}$$

第一个方程的关键点是：$row\ 1$和$x$正交。他们的内积是零，对于每个方程，右边都是零，所以$x$与每行都正交，因此$x$与行的各种组合正交。零空间中的$x$与行空间中的每个向量都是正交的，所以$N(A)\perp C(A^T)$。

另一对正交子空间来自$A^Ty=0$或者$y^TA=0$：

$$\begin{equation} y^TA=\begin{bmatrix} y_1&\cdots&y_m \end{bmatrix} \begin{bmatrix} c&&c\\o&&o\\l&&l\\u&\cdots&u\\m&&m\\n&&n\\1&&n \end{bmatrix} =\begin{bmatrix} 0&\cdots&0 \end{bmatrix}\tag7 \end{equation}$$

向量$y$和每个列正交，根据方程可以看出，右边全是零，因此$y$和列的所有组合是正交的。它正交于列空间：$N(A^T)\perp C(A)$，用$A$替换$A^T$后就跟前面的一模一样了。

证明2：和无坐标的证明进行对比会非常有益，它将给出更加抽象的推理方法，我希望大家能够完全理解这个证明。

如果$x$在零空间里，那么$Ax=0$，如果$v$在行空间里，存在某个行的组合：$v=A^Tz$，那么

$$\begin{equation} v^Tx=(A^Tz)^Tx=z^TAx=z^T0=0\tag8 \end{equation}$$

例3：假设$A$的秩为1，那么它的行空间和列空间都是直线：

$$A=\begin{bmatrix} 1&2\\2&6\\3&9 \end{bmatrix}$$

行是$(1,3)$的倍数，零空间包含$x=(-3,1)$，它和所有的行正交，零空间和行空间是$R^2$中正交的两条直线：

$$\begin{bmatrix} 1&3 \end{bmatrix} \begin{bmatrix} 3\\-1 \end{bmatrix} =0\quad \begin{bmatrix} 2&6 \end{bmatrix} \begin{bmatrix} 3\\-1 \end{bmatrix} =0\quad \begin{bmatrix} 3&9 \end{bmatrix} \begin{bmatrix} 3\\-1 \end{bmatrix} =0$$

与此相反，其他的两个子空间在$R^3$中，列空间是通过$(1,2,3)$的直线，左零空间肯定垂直于平面$y_1+2y_2+3y_3=0$，这个方程也就是$y^TA=0$。

前两个子空间的维数为$1+1=2$，后两个子空间维数为$1=2=3$。一般情况下，行空间和零空间维数加起来为$r+(n-r)=n$，另外两个空间为$r+(m-r)=m$，除了正交外还发生了其他事，也就是维数。

毫无疑问，零空间垂直于行空间——但是它不是全部事实。$N(A)$包含了所有垂直于行空间的向量，因为零空间是由$Ax=0$的所有解组成的。

定义：给定$R^n$的一个子空间$V$，所有和$V$垂直的向量组成的空间叫做$V$的正交补，用$V^{\perp}$表示。

利用这个术语，零空间是行空间的正交补：$N(A)=(C(A^T))^{\perp}$，同时行空间包含所有与零空间垂直的向量。位于行空间外的向量$z$不可能和零空间正交，因为加上$z$作为$A$的额外行的话会扩大行空间，但是我们知道有一个固定的等式$r+(n-r)=n$：

$$dim(\text{行空间})+dim(\text{零空间})=\text{列数}$$

每个正交于零空间的向量都在行空间内：$C(A^T)=(N(A))^{\perp}$。

同样的推理应用到$A^T$上得到对偶的结果：左零空间$N(A^T)$和列空间$C(A)$是正交补的关系。他们的维数加起来$(m-r)+r=m$，至此就完成了线性代数基本定理得第二部分。第一部分给出四个子空间的维数，包括列的秩等于行的秩。现在我们还知道他们是垂直的，不仅如此，他们还是正交补的关系。

4、线性代数基本定理：零空间是行空间的正交补；左零空间是列空间的正交补。
再强调一下，行空间包含所有正交零空间的向量，列空间包含所以正交左零空间的向量。对于$Ax=b$，我们能直接看出方程要成立$b$必须在列空间，但思考一下会发现，要成立的话$b$必须与左零空间垂直。

5、方程$Ax=b$，$y^TA=0$，那么当且仅当$y^Tb=0$时是方程可解。

最直接的方法是$b$是列的组合，间接的方法是$b$必须与列正交的每个向量正交。这个方法不太直观，但是如果只有一个或两个向量和列正交的话，它很容易检查$y^Tb=0$是否成立，前面讲的基尔霍夫电压定律就是很好的例子，测试闭环为零比识别列的组合更加容易。

当$Ax=b$的左边加起来为零时，右边也必须为零：

$$\begin{matrix} x_1&-&x_2&=&b_1\\x_2&-&x_3&=&b_2\\x_3&-&x_1&=&b_3 \end{matrix} \text{是可解的，当且仅当} b_1+b_2+b_3=0\quad A=\begin{bmatrix} 1&-1&0\\0&1&-1\\-1&0&1 \end{bmatrix}$$

测试$b_1+b_2+b_3=0$可以知道$b$正交左零空间的$y=(1,1,1)$，根据基本定理，$b$是列的一个组合！

矩阵和子空间

我们强调$V,W$是正交的，但是不是正交补。他们的维数太小，由$(0,1,0)$生成的线空间$V$与$(0,0,1)$生成的线空间$W$是正交的，但是$V$不是$W^{\perp}$。当维数正确的时候，正交子空间才可能是正交补：

$$\text{如果}W=V^{\perp},\text{那么}V=W^{\perp}\text{并且}dimV+dimW=n$$

也就是说$V^{\perp\perp}=V$，$V,W$的维数正确的话，整个空间$R^n$就能分解为两个垂直的部分(图3)。

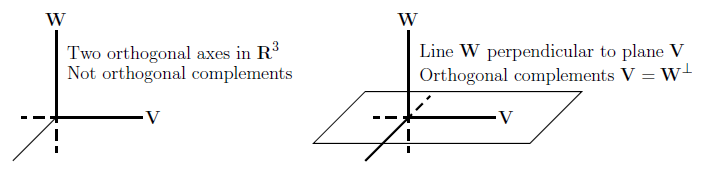
图3

将$R^n$分成正交的部分后，每个向量分成$x=v+w$，向量$v$ 是$x$在$V$上的投影，正交部分的$w$是$x$在$W$上的投影，下一篇文章我将介绍如何找出$x$的这些投影。

图4总结了线性代数的基本定理，它给出了矩阵的实际效果—— 乘法$Ax$内部发生了什么。零空间变成零向量，每个$Ax$在列空间里，没有任何东西会变到左零空间里，实际操作发生在行空间和列空间之间，并且还能看到向量$x$，它由行空间的元素和零空间的元素组成，$x=x_r+x_n$。当用矩阵$A$相乘时，得到$Ax=Ax_r+Ax_n$:

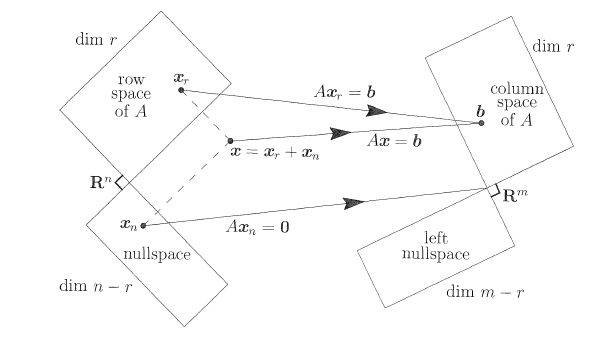
图4

1. 零空间的元素变成零：$Ax_n=0$。
2. 行空间的元素变到列空间里：$Ax_r=Ax$。

当然每个都进入到列空间——矩阵没有其他作用的。在图中我零行和列空间的大小相等，都等于维数$r$。

6、从行空间到列空间，$A$是可逆的。列空间中的每个$b$都来自行空间中的$x_r$。

证明：列空间中的每个$b$是列$Ax$ 的一个组合。事实上，$b$是$Ax_r$，其中$x_r$在行空间中，因为零空间的元素得到$Ax_n=0$。如果行空间的另一个元素$x_r^{'}$得出$Ax_r^{'}=b$，那么$A(x_r-x_r^{'})=b-b=0$。 这样的话$x_r-x_r^{'}$既在零空间又在行空间里，也就是自己和自己正交，因此只能是零。所以行空间中只要一个变量能变成$b$。

每个矩阵将它的行空间变到列空间。

$r$维空间上，$A$是可逆的，$A$的零空间为零。当$A$是对角矩阵时，我们将会看到有$r$个非零值的子矩阵是可逆的。

$A^T$方向相反，是从$R^m$到$R^n$，也就是$C(A)$到$C(A^T)$。当然转置不是逆！$A^T$移动的是空间而不是向量，这个操作需要$A^{-1}$来完成，当然前提是逆存在，也就是$r=m=n$。我们这里不探讨$A^{-1}$将零向量变成整个零空间的操作。

当$A^{-1}$不存在时，最好的替换是伪逆$A^{+}$。这就使$A$ 可逆了：$A^{+}Ax=x$，其中$x$位于行空间。而对于左零空间，什么都不需要做：$A^{+}y=0$。$A^{+}$的一种形式依赖于奇异值分解，为此我们需要知道特征值，后面会详细介绍。