漫步微积分三十五——弧长

弧是介于曲线上两个特定点$A$和点$B$之间的一部分，如图1 左边所示。物理上，弧长是一个非常简单的概念。数学上，它是稍微有点复杂。从物理观点看，我们只是折弯了一根绳子来拟合从$A$到$B$的曲线，标记下对应的点$A$和$B$，将绳子伸直然后用尺子量出长度。

这一过程可以用如下的逼近过程(适合于数学处理)来解决。弧$AB$用点$P_0=A,P_1,P-2,\ldots,P_n=B$分成$n$部分；将针放在这些点上；让该线段沿着这些一个个短针得到的路径延伸。我们在图1右边用$n=3$的情况说明了这个想法。$A,B$之间的长度明显短于弧长，因为两个点之间直线最短。然而，如果我们采取更大的$n$值，同时要求针之间放置的足够近，那么线的长度应该接近弧的长度。我们现在用数学语言表达它并推导出用积分计算弧长的实用方法。

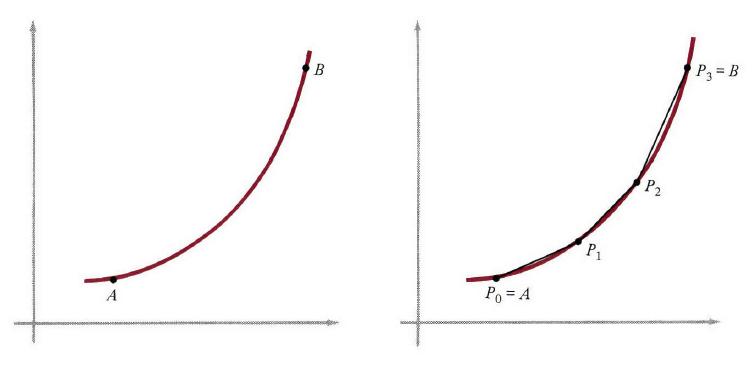
图1

假设下面讨论的弧是连续函数$y=f(x)$的在区间$a\leq x\leq b$上的图像。我们将区间$[a,b]$分成$n$个子区间，用点$x_0=a,x_1,\ldots,x_{k-1},x_k,\ldots,x_n=b$标记出来如图2所示。令$P_k$ 表示点$(x_k,y_k)$，其中$y_k=f(x_k)$。 多边路径$P_0P_1\cdots P_{k-1}P{k}\cdots P_{n}$的总长度是每个点之间弦长的长度和。如果我们写成

$$\Delta x_k=x_k-x_{k-1}\quad and\quad \Delta y_k=y_k-y_{k-1}\quad k=1,2,\ldots,n$$

那么利用毕达哥拉斯定理得

$$\begin{align} {\rm{length\ of\ kth\ chord}} &=\sqrt{(\Delta x_k)^2+(\Delta y_k)^2}\nonumber\\ &=\sqrt{\left[1+\frac{(\Delta y_k)^2}{(\Delta x_k)^2}\right](\Delta x_k)^2}\nonumber\\ &=\sqrt{1+\left(\frac{\Delta y_k}{\Delta x_k}\right)^2}\Delta x_k\tag1 \end{align}$$

现在我们假设函数$y=f(x)$不仅连续而且可导。那么我们就能用$x_{k-1},x_k$ 之间某点$x_k^*$处的导数值代替根号下的比值(也就是连接$P_{k-1},P_k$之间弦长的斜率)

$$\frac{\Delta y_k}{\Delta x_k}=f'(x_k^*)\quad x_{k-1}<x_k^*<x_k$$

这一步是基于这个事实：弦平行于曲线$P_{k-1},P_k$之间某点的切线。所以我们能将(1)写成

$${\rm{length\ of\ kth\ chord}} =\sqrt{1+[f'(x_k^*)]^2}\Delta x_k$$

所以总长度为

$$\begin{equation} \sum_{k=1}^n\sqrt{1+[f'(x_k^*)]^2}\Delta x_k\tag2 \end{equation}$$

现在我们用这些和的极限形式得出了结论，当$n$趋于无穷大时，最长子区间的长度接近零：

$$\begin{align} {\rm length\ of\ arc\ AB} &=\lim_{{\rm max\Delta x_k\to 0}}\sum_{k=1}^n\sqrt{1+[f'(x_k^*)]^2}\Delta x_k\nonumber\\ &=\int_a^b\sqrt{1+[f'(x)]^2}dx\tag3 \end{align}$$

因为$f'(x)$是连续的，所以它的积分存在。

首先，公式(3)不太好记。然而，如果我们用莱布尼兹符号$dy/dx$代替$f'(x)$，那么下面直觉的方法将令这个公式更加掌握和记忆。让$s$表示从$A$ 到曲线上某个变化点的弧长，如图3所示。$s$可以由一个很小的增量$ds$使得$ds$是弧长的微分元素，$dx,dy$分别是$x,y$对应的变化量。我们将$ds$看做非常小，小到这段曲线几乎是直的，因此$ds$是直角三角形(称为微分三角形)的斜边。根据毕达哥拉斯定理得

$$\begin{equation} ds^2=dx^2+dy^2\tag4 \end{equation}$$

这个简单的方程是计算弧长所有智慧的根源。如果我们求解(4)，因子$dx^2$提出来并移到根号外得

$$\begin{align} ds &=\sqrt{dx^2+dy^2}\nonumber\\ &=\sqrt{\left(1+\frac{dy^2}{dx^2}\right)dx^2}=\sqrt{\left(1+\frac{dy^2}{dx^2}\right)}dx\tag5 \end{align}$$

图2

弧$AB$的总长度可以看做所有弧元素$ds$从$A$到$B$的总和- 或积分。利用(5) 可以得出

$$\begin{equation} {\rm length\ of\ arc\ }AB=\int ds=\int_a^b\sqrt{\left(1+\frac{dy^2}{dx^2}\right)}dx\tag6 \end{equation}$$

也就是(3)。这个公式告诉我们$x$是积分变量，$y$可以看做$x$的函数。然而，有时候用$y$表示积分变量，将$x$看做$y$ 的函数会更加方便。在这种情况下(5) 可以换为

$$\begin{align} ds &=\sqrt{dx^2+dy^2}\nonumber\\ &=\sqrt{\left(\frac{dx^2}{dy^2}+1\right)dy^2}=\sqrt{\left(\frac{dx^2}{dy^2}+1\right)}dy\tag7 \end{align}$$

因为$y$是积分变量，弧长$AB$的积分是

$$\begin{equation} \int ds=\int_c^d\sqrt{\left(\frac{dx^2}{dy^2}+1\right)}dy\tag8 \end{equation}$$

有时候它比(6)计算更加简单。

例：求出曲线$y^2=4x^3$在点(0,0) 和$(2,4\sqrt{2})$ 之间的弧长。

解：曲线如图4所示

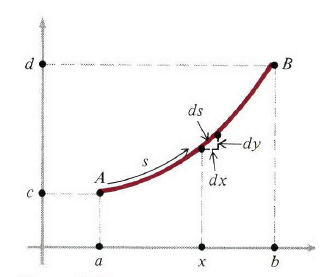
图3



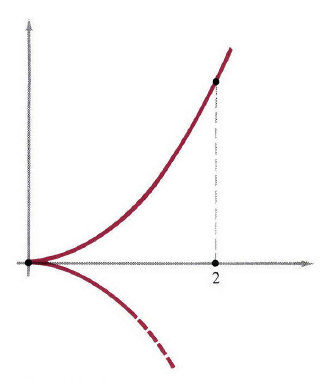
图4

问题中的弧指的是第一象限的曲线，如果我们求解$y$，那么得到

$$y=2x^{3/2}\quad so\quad \frac{dy}{dx}=3x^{1/2}$$

那么公式(6)变为

$$\begin{align*} {\rm length\ of\ arc\ } &=\int_0^2\sqrt{1+9x}=dx=\frac{1}{9}\int_0^2(1+9x)^{1/2}9dx\\ &=\frac{1}{9}\cdot \frac{2}{3}(1+9x)^{3/2}\Big|_0^2=\frac{2}{27}(19\sqrt{19}-1) \end{align*}$$

对这种计算应该提出一个警告，当我们尝试求解任何熟悉曲线的弧长时，因为(6)中有平方根，所以我们可以无法求出积分。目前，我们是为了能够计算出积分，仔细选择了我们的问题。但这也同时让我们意识到我们迫切需要更多的积分方法。我会在下三篇文章中说明。

注解1：存在这样的例子，在$a\leq x\leq b$ 上曲线$y=f(x)$ 连续，但是没有长度。这个令人吃惊的事实表明弧长的基本理论比我们想象的要复杂得多。我们的讨论都需要假定函数$y=f(x)$有连续的导数。这种曲线称为光滑曲线，并且”弧”一词通常意味着限制曲线有这种属性。一条光滑曲线在几何上通常描述为”连续的转向切线”。

注解2：一些学生对方程(4)和(5)可能存在这样的印象(他们互相等效)他们是近似解，大概正确，因为微分三角形只是“准三角”，实际所谓的斜边不是一条真正的直线段。可事实不是这样的，这些方程完全正确。我们知道(3)是有效的，所以图3中的弧长$s$可以写成

$$s=\int_a^x\sqrt{1+[f'(t)]^2}dt$$

用$t$表示积分变量。很明显$s$是积分上限为$x$的函数，我们计算它的导数得

$$\frac{ds}{dx}=\sqrt{1+[f'(x)]^2}=\sqrt{1+\left(\frac{dy}{dx}\right)^2}$$

和等式(5)等价。