线性模型

y=wx+b

优点：可解释性强；非线性模型可以通过在线性模型的基础上引入层级结构或者高维映射而得。

 

将特征转化为模型的输入值

离散属性：如果存在序关系（高中低），可以将其转化为对应的连续值；如果不存在序关系（不太相关的值），则可以将其转化为k维向量，k为属性的取值个数。

 

性能度量：均方误差最小化，对应的方法称为“最小二乘法”。

 

如果xTx是一个满秩矩阵的话，那么w能够得到一个闭式解，如下：

 

但是现实任务中有很多变量数大于样例数的情况，导致矩阵并不满秩，所以会有多个w的解。这种情况下就要引入正则化项来挑选。

 

广义线性模型：

当g取为ln时上式变为对数线性回归。

 

对数几率函数（逻辑回归函数）：

     =>> 

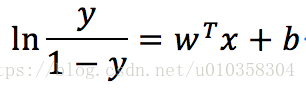
y代表样本为正例的可能性，（1-y）代表样本为反例的可能性，所以上图右侧为x为正例的对数几率（所谓几率指x作为正例的相对可能性）。   虽然上式通常被称为逻辑“回归”，但其实为分类模型，而不是回归模型。直接对分类可能性建模，得到的y值对应为类别的概率预测。

 

LDA: linear discriminant analysis 线性判别分类器  将样例投影到一条直线上，使得同类的投影点尽可能接近，异类投影点尽可能远离。 分类时，将待预测样本也投影到直线上，根据距离远近判断其类别。

 

多分类学习：将多分类拆分为若干个二分类任务求解，为拆分出的每个二分类任务训练一个分类器。

如何拆分：

1） 一对一：将类别两两配对，将其中一个作为正类，一个作为负类，训练分类器。

2）一对其余：将一个类作为正例，其余所有类作为负类，训练分类器。只需训练N个分类器。

3）多对多：将若干个类作为正类，若干个类作为反类

 

类别不平衡：正反例的比例不对等。当正例小于反例时，解决方法：

1）对反例欠采样：去除一些反例，使得正反例子数目接近

2）对正例过采样：增加一些正例使得正反例子数目接近

3）直接基于原始训练集进行学习，但在使用训练好的分类器进行预测时进行再缩放，也就是阈值移动。也就是在均衡时使用y/(1-y)与1的比较作为判断正负例的标准，但在不均衡时应该使用样本中正负例子的比值来代替1作为阈值