人工智能-过拟合,欠拟合以及模型泛化

最新推荐文章于 2024-01-07 02:05:56 发布

路灯捶背三百一位

最新推荐文章于 2024-01-07 02:05:56 发布

阅读量792

点赞数

分类专栏： Ridge LASSO 逻辑回归文章标签：机器学习

本文链接：https://blog.csdn.net/u010473886/article/details/106686658

版权

逻辑回归同时被 3 个专栏收录

2 篇文章 0 订阅

订阅专栏

Ridge

1 篇文章 0 订阅

订阅专栏

LASSO

1 篇文章 0 订阅

订阅专栏

过拟合、欠拟合与模型泛化

这篇文章包含的内容比较多，我将从多项式回归模型中引出过拟合、欠拟合、模型泛化问题以及Ridge回归、LASSO回归两个用于优化过拟合问题的模型

多项式回归

在之前我们提到过简单线性回归、多元线性回归；都是假设特征与样本目标值之间是存在线性关系的，但实际应用中存在简单线性关系的场景是少之又少的；
如果特征与目标值是非线性关系，回归线是一条曲线，即目标值与某个或多个特征之间存在幂函数的关系，如何预测目标值呢？这就出现了多项式回归；
多项式回归的实现方式很简单，既然我们假设目标值与特征存在高次幂的关系，那么我们可以将所有特征求出幂函数值，作为新的特征添加到特征中，也就是对数据进行升纬；
$例： y = ax^2 + bx + c$
假设如上的二次函数模型，特征纬度为1，即 x；我们可以将 $x^2$ 看作一个新的特征 $x_1 = x^2$ ，这样就相当于特征纬度变为2，
$y = ax_1 + bx_2 + c$
舒服了～
然后用多元线性回归模型来训练，得到各个特征的 $\theta$ 系数，这样就实现了多项式回归

这里我们生成一个训练数据集

import matplotlib.pyplot as plt
import numpy as np

X = np.arange(-10,10,.1).reshape((-1,1))
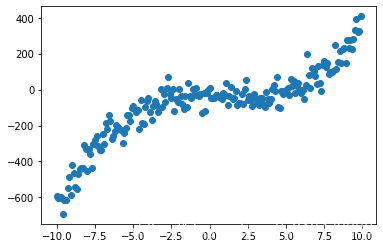
# 目标值与 x 特征之间的关系  y = 0.5x^3 - x^2 + x + 5 + 噪音
y = .5 * X[:,0]**3 - X[:,0]**2 + X[:,0] + 5 + np.random.normal(-50,50,200)
plt.scatter(X,y)

最终绘制出来的是这样，就像《野狼disco》里面的彩虹
在这里插入图片描述
接下来我们使用 sklearn 为我们提供的 Pipeline 将数据特征堆叠、数据归一化、线性回归组装到一起，就构成了一个可以训练 多项式回归模型 的函数

PolynomialFeatures 用于将特征进行升纬，构造函数传入 degree 表示将特征的最多几次方添加到特征中
StandardScaler 数据归一化，用于统一特征量纲
LinearRegression 线性回归

# 将数据样本分为 训练数据集 和 测试数据集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y)
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

def polynomialFeatures(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("scaler", StandardScaler()),
        ("linear_reg", LinearRegression())
    ])

过拟合、欠拟合、泛化能力

我们手动生成的训练数据集中，我们知道 y 与 x 是存在最高三次方的关系
下面，我会分别使用 1次方、平方、三次方以及三十次方来尝试进行训练
进而阐述过拟合和欠拟合现象

# 1次方
poly1 = polynomialFeatures(degree=1)
poly1.fit(X_train, y_train)
y_pre1 = poly1.predict(X_train)
plt.scatter(X,y)
plt.plot(np.sort(X_train[:,0]), y_pre1[np.argsort(X_train[:,0])],color = "red")
plt.title("R_Squared: {}".format(poly1.score(X_test, y_test)), color="red")

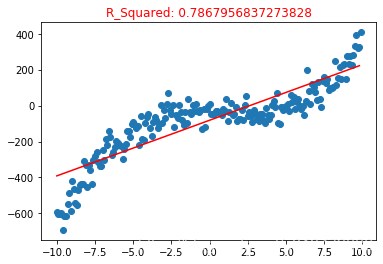
在这里插入图片描述
由于使用特征最高 1次方，相当于是简单线性回归来，所以回归线是一个直线
使用R_Squared 模型准确的评估，准确度为 0.786 的样子，完全一副人工智障的样子
这就是欠拟合的结果，我们训练数据集中，特征与目标值是最高三次方的关系，但是我们训练的模型是一次方关系，换句话说这个模型并不能完整的表达特征与目标值之间的关系，所以模型准确度只有 0.7

下面是平方的多项式回归模型

poly2 = polynomialFeatures(degree = 2)
poly2.fit(X_train, y_train)
y_pre2 = poly2.predict(X_train)

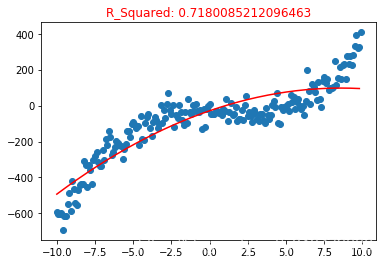
plt.title("R_Squared: {}".format(poly2.score(X_test, y_test)),color = "red")
plt.scatter(X,y)
plt.plot(np.sort(X_train[:,0]),y_pre2[np.argsort(X_train[:,0])],color = "red")

使用含有特征平方值的训练数据集训练的模型，有一点曲线的样子了
But ! 但是！ However !
R_2 模型准确度评估结果为 0.71 比一次方还要低，从图像来看又是一个欠拟合的产物
在这里插入图片描述

下面是最高三次方的训练数据集训练的多项式回归模型，这跟我们生成的规则是一致的

poly3 = polynomialFeatures(degree = 3)
poly3.fit(X_train, y_train)
y_pre3 = poly3.predict(X_train)

plt.title("R_Squared: {}".format(poly3.score(X_test, y_test)), color="red")
plt.scatter(X,y)
plt.plot(np.sort(X_train[:,0]), y_pre3[np.argsort(X_train[:,0])],color = "red")

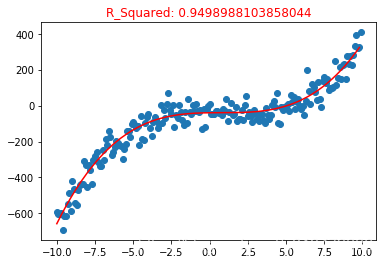
在这里插入图片描述
**excellent! **
训练出来的模型至少从视觉上完美的拟合了样本，R_2 模型准确度评估也达到了 0.94

模型误差 = 偏差 + 方差 + 无法避免的误差

由于训练数据集生成过程中我们加入了噪音，所以误差是客观存在的

接下来我们再看一下过拟合的情况, 这次我们使用特征最高30次方的值，作为新的特征加入训练数据集

poly5 = polynomialFeatures(degree =30)
poly5.fit(X_train, y_train)
y_pre5 = poly5.predict(X_train)

plt.title("R_Squared: {}".format(poly5.score(X_test, y_test)), color="red")
plt.scatter(X,y)
plt.plot(np.sort(X_train[:,0]), y_pre5[np.argsort(X_train[:,0])],color = "red")

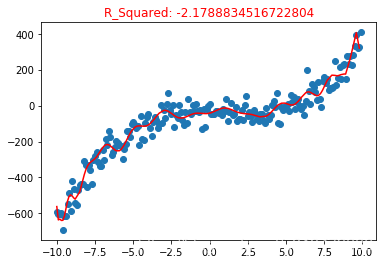
在这里插入图片描述
这个回归曲线非常花里胡哨，弯弯绕绕，好像拟合的非常棒，但是使用测试数据集进行模型准确度评估 R_2 = -2.17 ，当R_2 模型准确度为负数时，可以理解为模型完全是错的，甚至不如使用平均值作为模型进行预估；

泛化能力

我们明明看曲线拟合的还不错，为什么R_2 指标这么低呢，原因就在于过拟合：对训练样本拟合的很好，但是应用到生产环境，碰到新的样本预测结果表现的很差，模型把一些无关的特征学习到了，这就是过拟合情况，同时也表现出模型的泛化能力较低，难以将模型泛化到新的样本上

学习曲线

我们来绘制上面几个模型的学习曲线；随着训练样本数量增加，模型对训练样本预测误差和测试样本预测误差的变化趋势，进一步说明过拟合，欠拟合，以及泛化能力

下面几张图中 X 轴为训练样本的数量， Y轴为 MSE（均方误差）用于衡量预测值与实际值的误差，误差越大，可理解为模型准确度越低；
每幅图有两条线，没别表示模型对训练数据集预测的误差和泛化到训练数据集中不存在的样本后预测误差

from sklearn.metrics import mean_squared_error
# 绘制模型学习曲线
def drawLearnLinear(func, X, y):
    X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3)
    train_mse = np.empty(len(X_train))
    test_mse = np.empty(len(X_train))
    for i in range(len(X_train)):
        func.fit(X_train[:(i+1)], y_train[:(i+1)])
        train_mse[i] = mean_squared_error(y_train[:(i+1)], func.predict(X_train[:(i+1)]))
        test_mse[i] = mean_squared_error(y_test, func.predict(X_test))
    plt.plot(np.arange(len(X_train)), train_mse, label = "train line")
    plt.plot(np.arange(len(X_train)), test_mse, label = "test line")
    plt.axis([0,len(X_train),0, 50000])
    plt.legend()

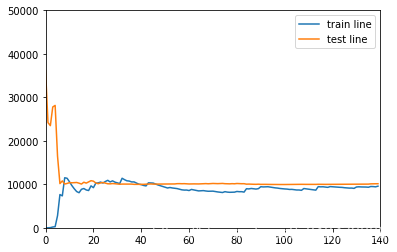
一次方的模型学习曲线（欠拟合）

drawLearnLinear(poly1,X,y)

如下图随着训练样本数量增加，两个误差最后稳定在 10000多一点，但是两条线间距逐渐减小，说明泛化能力还可以
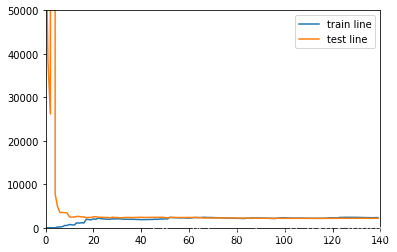
在这里插入图片描述

三次方的模型学习曲线

drawLearnLinear(poly3,X,y)

这幅图简直完美，

随着训练样本增加，两条线几乎合并，模型泛化能力很好，说明模型在训练样本训练后泛化到新的样本上，误差几乎一致
最终误差稳定在3000 左右的样子，相比上一幅图小了很多，相比较之下也说明上面的模型欠拟合

在这里插入图片描述

30次方的模型学习曲线

drawLearnLinear(poly5,X,y)

训练样本和测试样本之间间距很大并且测试样本误差非常不稳定，大出天际，过拟合，泛化能力较低

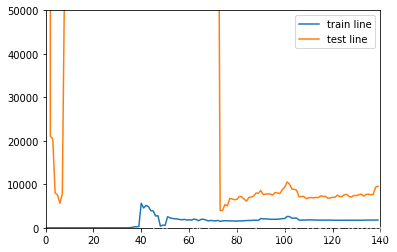
在实际应用过程中，我们大都是在解决过拟合情况，我们使用训练数据集训练模型，然后发现拟合的不错，即使发生过拟合也不自知，在高纬度的样本空间中，可是很难以进行可视化；所以接下来我们讨论如何解决过拟合

我们打印上面几个模型，学习到的 $\theta$ 参数

poly1.get_params()['linear_reg'].coef_

array([  0.        , 186.11946548])

poly2.get_params()['linear_reg'].coef_

array([  0.        , 163.6013378 , -50.05769662])

poly3.get_params()['linear_reg'].coef_

array([  0.        ,   2.00832969, -37.03488194, 208.61357956])

poly5.get_params()['linear_reg'].coef_

array([ 3.60460115e+12, -7.50492893e+01,  4.02625575e+02,  7.50064206e+03,
       -5.31983387e+04, -1.89716199e+05,  1.86114685e+06,  1.97519240e+06,
       -3.09333497e+07, -7.12811683e+06,  2.96235084e+08, -3.19140561e+07,
       -1.80711808e+09,  4.60268720e+08,  7.44470660e+09, -2.33671288e+09,
       -2.14435003e+10,  7.02475143e+09,  4.39978121e+10, -1.38712963e+10,
       -6.46641554e+10,  1.85250937e+10,  6.75581331e+10, -1.66255368e+10,
       -4.89684824e+10,  9.62439487e+09,  2.34009853e+10, -3.25078340e+09,
       -6.62797198e+09,  4.87070189e+08,  8.42481030e+08])

可以发现过拟合的模型，学习到的特征系数绝对值都非常大，那么我们是否通过限制 $\theta$ 的大小，来避免过拟合情况发生呢

答案是肯定的，我们可以在最小化损失函数过程中，最小化 $\theta$ ，在多元线性回归的损失函数后面添加一项
$\alpha \frac 1 2 \displaystyle \sum_{i=1}^n \theta_i^2$
或者
$\alpha \frac 1 2 \displaystyle \sum_{i=1}^n |\theta_i|$

然后最小化损失函数， $\alpha$ 也是新增的超参数，在我理解是用来控制 $\theta$ 在损失函数中的影响比重

两种不同的回归模型损失函数如下：

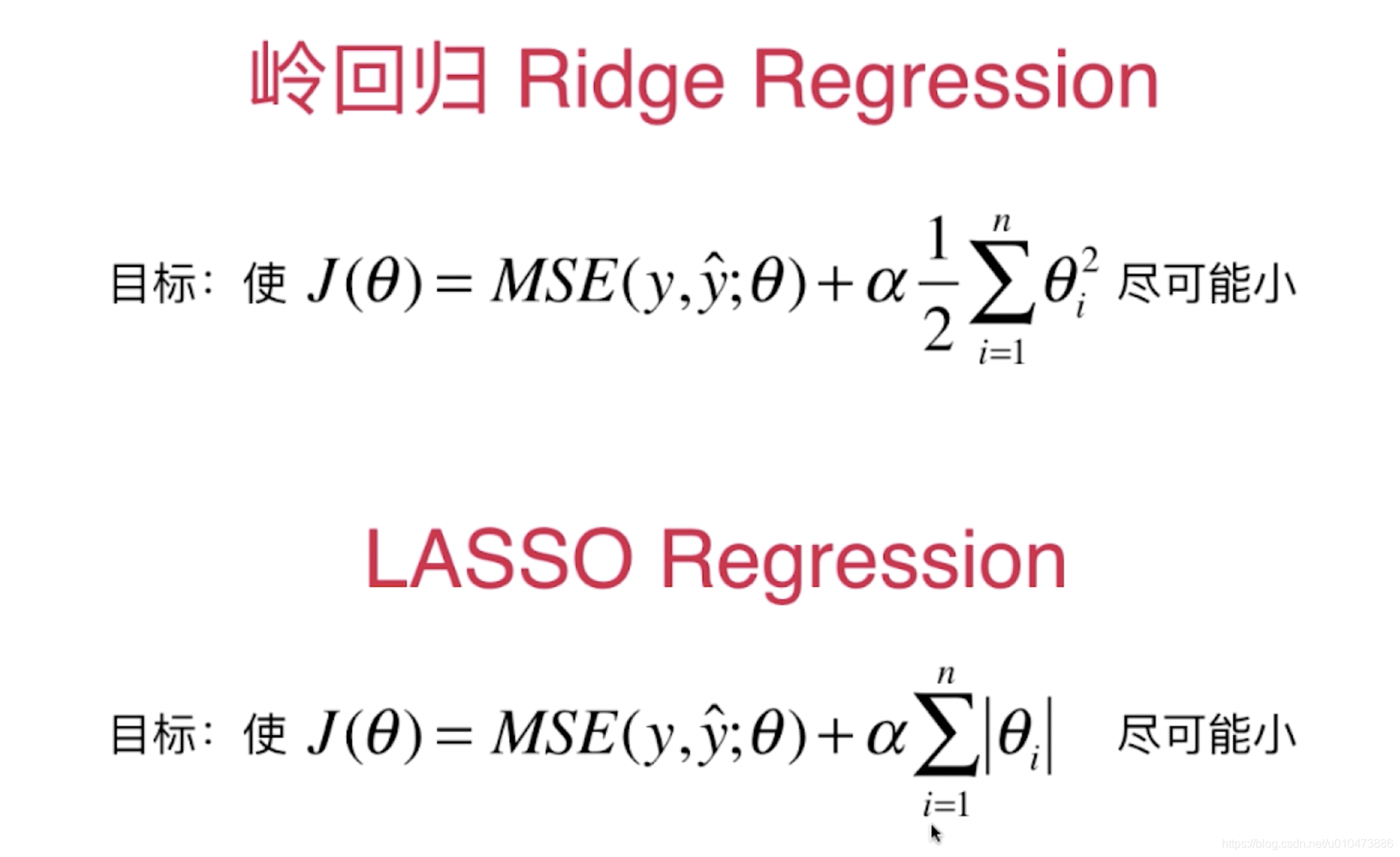
在这里插入图片描述

尝试使用Ridge回归、 LASSO回归解决过拟合

Ridge 回归

from sklearn.linear_model import Ridge
def ridgeFeatures(degree,alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("scaler", StandardScaler()),
        ("linear_reg", Ridge(alpha = alpha))
    ])

直接使用 30次方，可能存在过拟合情况来看一下Ridge回归的威力

ridge = ridgeFeatures(30,1)

ridge.fit(X_train, y_train)

print("模型预测准确度:",ridge.score(X_test,y_test))

模型预测准确度: 0.9557567126123063

再次绘制学习曲线

drawLearnLinear(ridge, X, y)

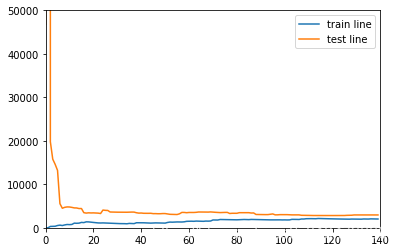
在这里插入图片描述
神奇的事情发生了，R_2 模型准确度达到了0.95，并且误差和泛化能力都不错，这可是包含各个特征30次方的训练数据集！

LASSO回归

from sklearn.linear_model import Lasso

def lassoFeatures(degree,alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("scaler", StandardScaler()),
        ("linear_reg", Lasso(alpha = alpha))
    ])

使用可能存在过拟合情况的超参数

lasso = lassoFeatures(30, 10)
lasso.fit(X_train,y_train)
print("模型预测准确度:",lasso.score(X_test,y_test))

模型预测准确度: 0.9447394073618249

绘制学习曲线

drawLearnLinear(lasso, X, y)

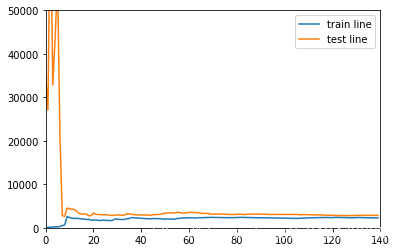
在这里插入图片描述
perfect!

路灯捶背三百一位

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
人工智能-过拟合,欠拟合以及模型泛化

这篇文章包含的内容比较多，我将从多项式回归模型中引出过拟合、欠拟合、模型泛化问题以及Ridge回归、LASSO回归两个用于优化过拟合问题的模型
复制链接

扫一扫

专栏目录

人工智能-过拟合,欠拟合以及模型泛化

过拟合、欠拟合与模型泛化

多项式回归

过拟合、欠拟合、泛化能力

学习曲线

尝试使用Ridge回归、 LASSO回归 解决过拟合

Ridge 回归

LASSO回归

“相关推荐”对你有帮助么？

尝试使用Ridge回归、 LASSO回归解决过拟合