1th Nov,金融数据作业

金融数据分析第一次作业

1.1题

• 分析

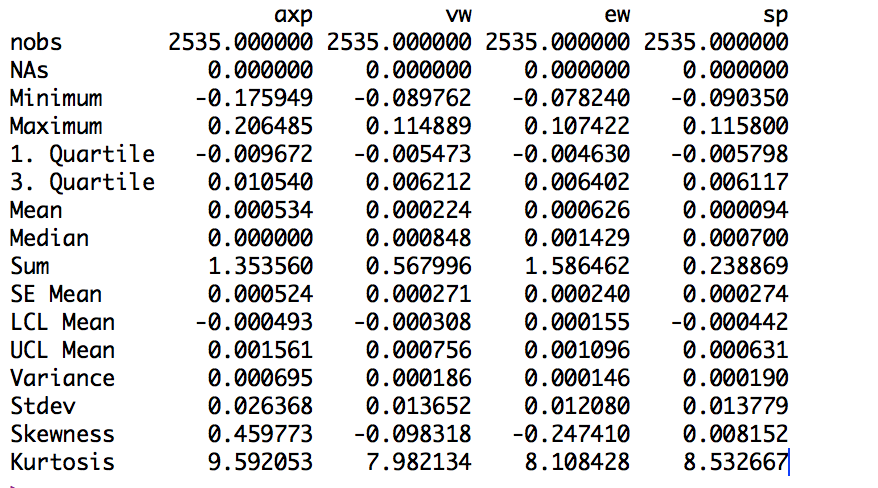
（1）我们使用fBasics进行简单收益率的描述性统计；
（2）分析简单收益率与对数收益率的关系，我们有
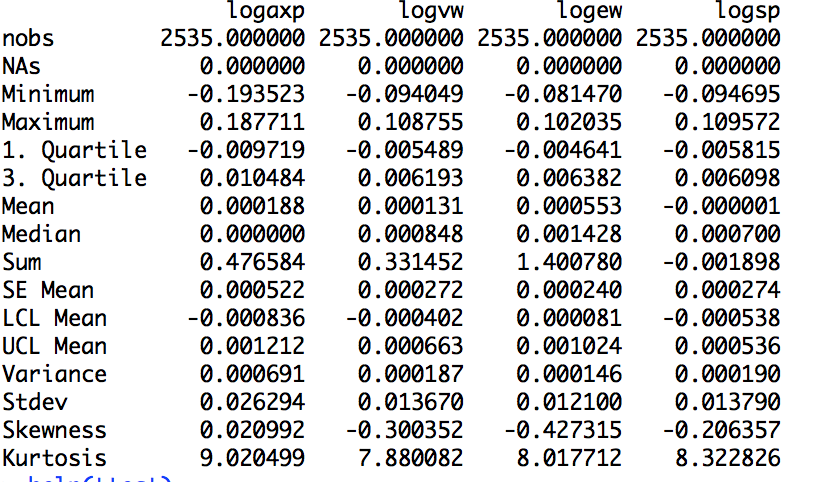
$logR=log(R+1)$,将转换的数据用该包进行的描述性统计；
（3）使用R语言自带的t.test进行t检验；

• 代码

library('fBasics')
axp<-read.table("/Users/ZHU/Desktop/学习资料/金融数据分析/data/ch1data/d-axp3dx-0111.txt",header=T);
logaxp<-log(axp$axp + 1);
logvw<-log(axp$vw + 1);
logew<-log(axp$ew + 1);
logsp<-log(axp$sp + 1);
logdata<-cbind(axp$date,logaxp,logvw,logew,logsp);
logdata<-as.data.frame(logdata)；
smry<-basicStats(logdata[,c(2,3,4,5)])
t.test(logdata$logaxp)

• 结果
  简单收益率的各项统计指标：
  
  对数收益率：
  
  t检验结果：
  
One Sample t-test
data: logdata$logaxp
t = 0.35999, df = 2534, p-value = 0.7189
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.0008360686 0.0012120714
sample estimates:
mean of x
0.0001880014
``
  从结果来看，axp的对收益率在95％的置信区间内，不能拒绝原假设，我们认为其收益率可以认为是零。
  1.3题

• 分析
  对这三个指标分别进行t-test，其中偏度和峰度的检验需要根据其枢轴量的分布自己构造t-statistics，在计算p值时我用了正态分布的分位数，在数据量较大时我们知道t分布是渐进趋向正态分布的。

• 代码

 library("timeDate")
library("timeSeries")
library('fBasics')
ge<-read.table("/Users/ZHU/Desktop/学习资料/金融数据分析/data/ch1data/m-ge3dx-4011.txt",header=T);
t.test(ge)
skewtest(ge)
kurtuosis_test(ge)
skewtest <- function(ts){
    s <- skewness(ts)
    T <- length(ts)
    if(T < 30)
        print("Warning:insufficient sample,the p-value may heavily biased!")
    t3 <- s/sqrt(6/T)
    pp <- 2*(1 - pnorm(t3))
    return(pp)
}

kurtuosis_test <- function(ts){
    s <- kurtosis(ts)
    T <- length(ts)
    if(T < 30)
        print("Warning:insufficient sample,the p-value may heavily biased!")
    t4 <- s/sqrt(24/T)
    pp <- 2*(1 - pnorm(t4))
    return(pp)
}

• 结果
  我们算得三个指标的P值分别为：3.386e-06，0.5363498，1.136868e-13，所以我们得到结论收益率序列收益率显著不为零，但是没有明显的不对称，但是显著厚尾。

2.1
(a)我们将失业率画出来，发现是一个有截距没有趋势的图形，所以我们选定了ADF检验的方法，使用ar模型拟合确定阶数为11阶，代码如下：

library("urca")
library("fUnitRoots")
uepm<-read.table("/Users/ZHU/Desktop/学习资料/金融数据分析/data/ch2data/m-unrate-4811.txt",head=T)
urate <- uepm$rate
plot(urate,type="l")
acf(urate);pacf(urate)
m1 <- ar(diff(urate),method='mle');
adfTest(urate,lags=m1$order,type(c("c")));

得到的结果为：

itle:
 Augmented Dickey-Fuller Test

Test Results:
  PARAMETER:
    Lag Order: 12
  STATISTIC:
    Dickey-Fuller: -2.72
  P VALUE:
    0.07501  

所以我们知道，不能拒绝原假设，说明我们不能拒绝这是一个单位根过程的假设。

(b)首先对失业率画出ACF与PACF图，发现ACF拖尾而PACF截尾，但是ACF表现为收敛于零的速度非常的慢，100阶后才不显著异于0。
尝试长记忆模型，模型拟合非常显著。代码如下：

library("TSA")
durate<-diff(urate)
m1=ar(durate,method="mle")
m1$order
print(durate$aic,digits=3)
m2=arima(x=urate,order=c(12,1,0),fixed=c(0,NA,NA,NA,NA,0,0,0,0,NA,0,NA))
tsdiag(m2)
test<-Box.test(m2$residuals,lag=30,type='Ljung')
1-pchisq(test$X-square,24)
m4=fracdiff(urate,nar=1,nma=1)
summary(m4)

差分方程的结果是：

Call:
  fracdiff(x = urate, nar = 1, nma = 1) 
Coefficients:
    Estimate Std. Error z value Pr(>|z|)    
d  0.2648840  0.0009471  279.69   <2e-16 ***
ar 0.9650814  0.0368789   26.17   <2e-16 ***
ma 0.1561706  0.0096425   16.20   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
sigma[eps] = 0.2070408 
[d.tol = 0.0001221, M = 100, h = 1.268e-06]
Log likelihood: 119.3 ==> AIC = -230.6804 [4 deg.freedom]

但是差分不能预测，所以我们还是要用airma建模，首先对原始数据进行差分，然后通过AIC给模型定阶，我们看到：

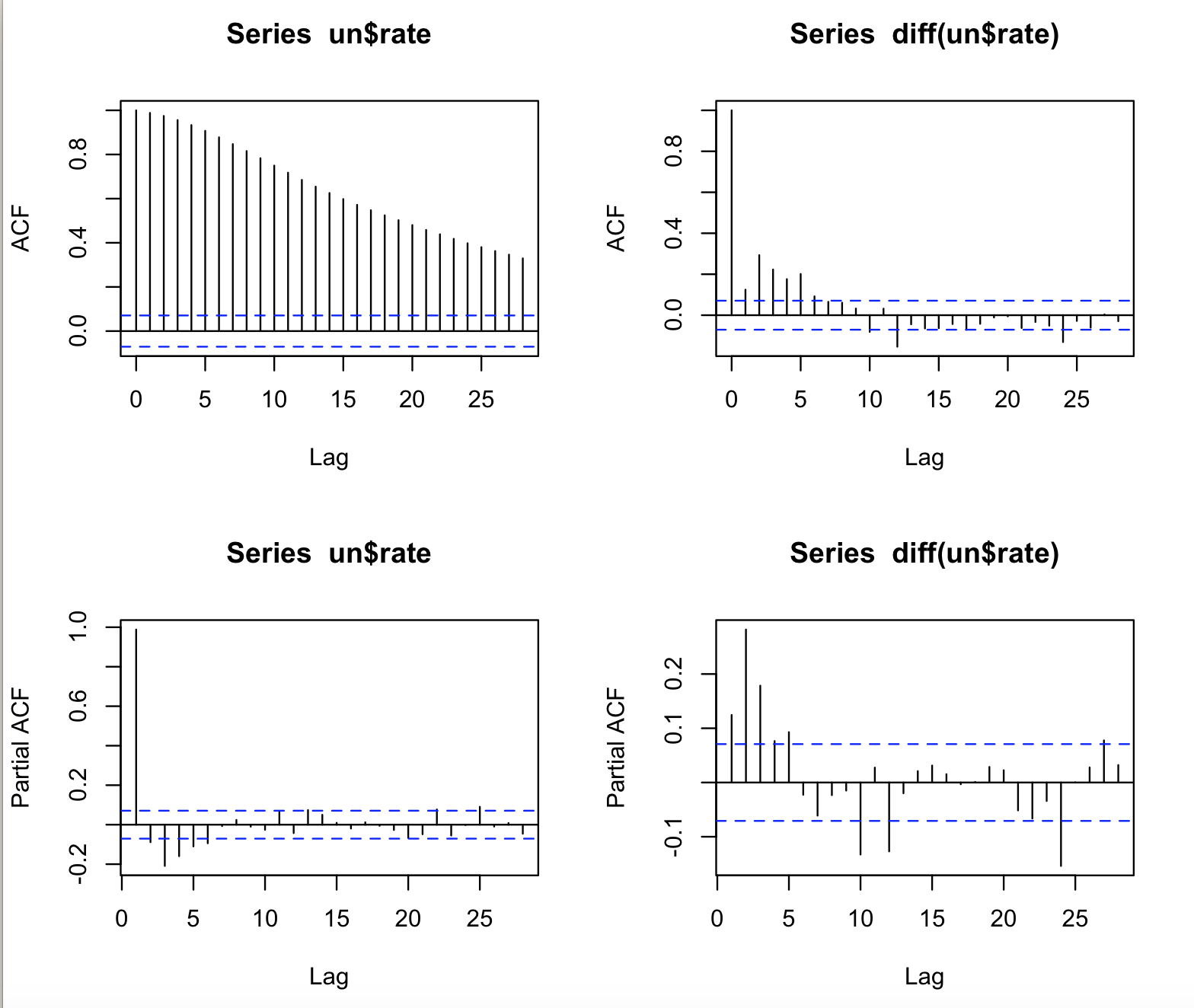
差分的后的图有明显的12阶周期性，再结合ACF5阶显著，PACF指数衰减，我们建立的模型为：$ARIMA(1,1,5)(1,0,1)^{12}$
观察第一次回归后系数的显著效果，结果为：

Call:
arima(x = da$rate, order = c(1, 1, 5), seasonal = list(order = c(1, 0, 1), period = 12), 
    include.mean = F, fixed = c(NA, NA, NA, 0, 0, NA, NA, NA))

Coefficients:
         ar1      ma1     ma2  ma3  ma4     ma5    sar1     sma1
      0.7536  -0.7744  0.2351    0    0  0.0990  0.6051  -0.8525
s.e.  0.0569   0.0650  0.0365    0    0  0.0386  0.0654   0.0457

sigma^2 estimated as 0.03649:  log likelihood = 175.75,  aic = -337.5

模型检验也是充分的，如图：

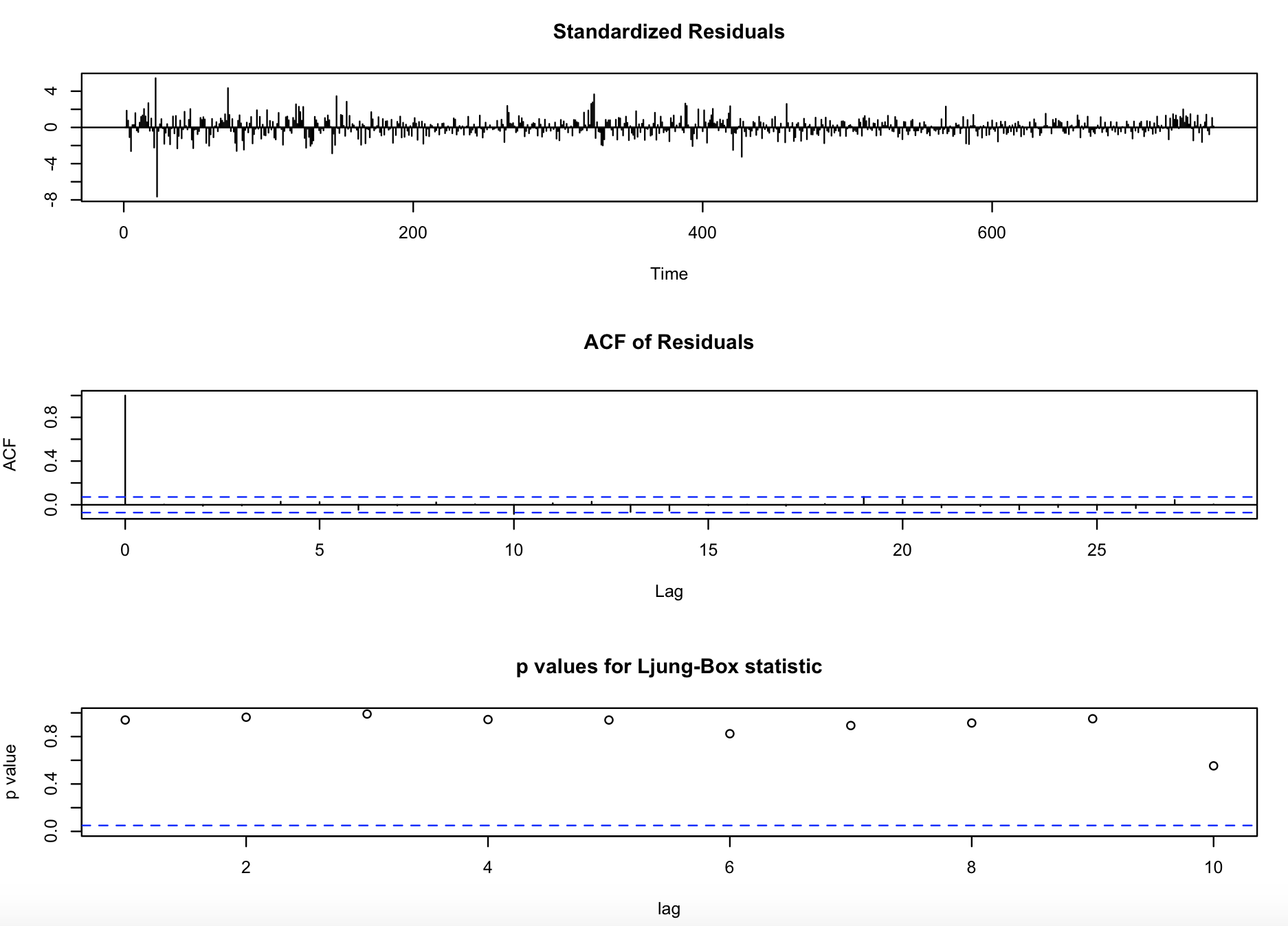
用模型进行4期预测有：

模型	1	2	3	4
Pred	9.513730	9.498022	9.384609	9.450147
s.e.	0.1910190	0.2673454	0.3519905	0.4379314

(c)存在商业周期，为12期。
2.2
(a)对数据进行Ljung-Box检验，我们得出结论，dec2不能拒绝ACF全为0，dec显著不为零。
(b)使用TSA包计算出dec2序列的EACF值，我们看图：

AR/MA
  0 1 2 3 4 5 6 7 8 9 10 11 12
0 x o o o o o o o o o o  o  o 
1 x o o o o o o o o o o  o  o 
2 x x o o o o o o o o o  o  o 
3 x o x o o o o o o o o  o  o 
4 x o x o o o o o o o o  o  o 
5 x x x x x o o o o o o  o  o 
6 x x o x o x o o o o o  o  o 

所以我们认为这个三角形的顶点在ARMA(0,1)的位置，对模型进行拟合，我们得到结果以及检验：

Call:
arima(x = crsp$dec2, order = c(0, 0, 1), method = "ML")

Coefficients:
         ma1  intercept
      0.1307     0.0093
s.e.  0.0425     0.0022

sigma^2 estimated as 0.002223:  log likelihood = 996.04,  aic = -1988.08

所以模型为 xt=0.0093+ϵt−0.1307