数据结构-（平衡二叉树，最短路径，关键路径）-含代码

本文链接：https://blog.csdn.net/u011146203/article/details/133949565

作业三-----平衡二叉树

二叉树

二叉树的逻辑结构

二叉树的定义

二叉树是n（n $\ge$ 0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

二叉树特点

1.每个结点最多有两颗子树。

2.二叉树是有序的，其次序不能任意颠倒。

注意：二叉树和树是两种树结构。

二叉树的基本性质

性质1:二叉树的第i层上最多有 $2^{i-1}$ 个结点（i $\ge$ 1）

性质2:一棵深度为k的二叉树中，最多有 $2^{k-1}$ 个结点，最少有k个结点。

性质3:在一棵二叉树中，如果叶子结点数为 $n_0$ ，度为2的结点数为 $n_2$ ，则有： $n_0=n_2+1$ 。

性质4:具有n个结点的完全二叉树的深度为 $\left\lfloor\log _{2} n\right\rfloor+1$ 。

性质5:对一棵具有n个结点的完全二叉树中从1开始按层序编号，则对于任意的序号为i（ $1\le i \le n$ ）的结点(简称为结点i），有：
（1）如果i>1，则结点的双亲结点的序号为i/2；如果i=1，则结点是根结点，无双亲结点。

（2）如果 $\le n$ ，则结点i的左孩子的序号为2i；如果2i>n，则结点i无左孩子。

（3）如果 $2i+1\le n$ ，则结点i的右孩子的序号为2i+1；如果 $2 i + 1 > n$ ，则结点无右孩子。

顺序存储结构

二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置（下标）应能体现结点之间的逻辑关系-父子关系。

完全二叉树的顺序储存

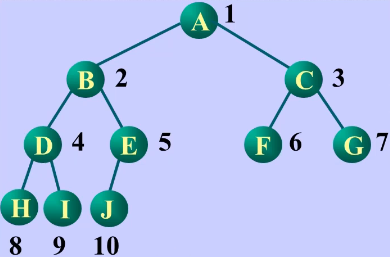
二叉树编号

按照完全二叉树编号

可以编号为：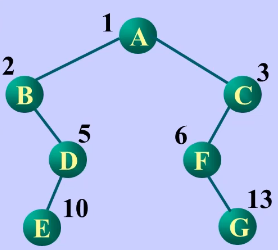

没有编号的位置直接存储为空。

二叉链表

data	数据域，存放该结点的数据信息
Ichild	左指针域，存放指针指向左孩子的指针
rchild	右指针域，存放指针指向右孩子的指针

class tree
{
    public:
    int data;
    class tree* Ichild;
    class tree* rchild;
}
typedef class tree node;
typedef node *btree;

二叉树的遍历

二叉树的组成：根结点D，左子树L，右子树R。

如果限定先左后右，则二叉树遍历方式有三种：

前序（Preorder）：DLR

中序（Inorder）：LDR

后序（Postorder）：LRD

如下图所视

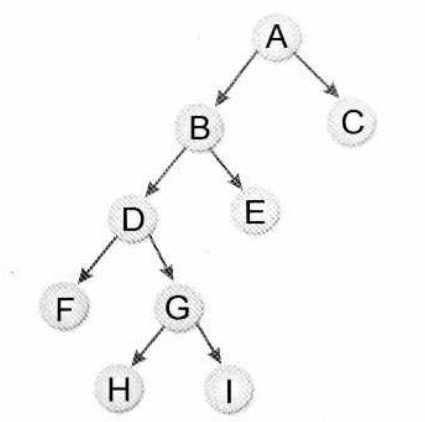
中序遍历

1.遍历左子树
2.遍历（或访问）树根
3.遍历右子树

中序遍历为：FDHGIBEAC

void Inorder(btree ptr)
{
if (ptr != NULL)
	{
	Inorder(ptr->left);   //遍历左子树
	cout<<ptr ->data;     //遍历并打印树根
	Inorder(ptr->right);   //遍历右子树
	}
}

后序遍历

1.遍历左子树
2.遍历右子树
3.遍历树根

中序遍历为：FHIGDEBCA

void Postorder (btree ptr)
{
if (ptr != NULL)
{
	Postorder(ptr->left);     //遍历左子树
	Postorder(ptr->right);    //遍历右子树
	cout<<ptr->data;          //遍历并打印树根
}

前序遍历

1.遍历树根
2.遍历左子树
3.遍历右子树

中序遍历为：ABDFGHIEC

void Preorder(btree ptr)
{
if (ptr != NULL)
	{
    cout<<ptr ->data;     //遍历并打印树根
	Inorder(ptr->left);   //遍历左子树
	Inorder(ptr->right);   //遍历右子树
	}
}

二叉树节点的插入和删除

在二叉树建立的过程中，是根据左子树<树根<右子树的原则建立的。

查找

只需从树根出发比较键值，如果比树根大就往右，否则往左而下，直到相等就找到了要查找的值，如果比到NULL，无法再前进就代表查找不到此值。

btree search (btree ptr,int val)  //查找二叉树某键值得函数
{
	while（1）
	{
		if(ptr==NULL)     //没找到就返回NULL
			return NULL;
		if(ptr->data==val)   //节点值等于查找值
			return ptr;
		else if(ptr->data>val)  //节点值大于查找值
			ptr=ptr->left;
		else                  //小于查找值
			ptr=ptr->right;    
	}
}

插入操作

插入节点的情况和查找相似，关键是插入后仍要保持二叉查找树的特性（左子树<树根<右子树）。如果插入的节点在二叉树中没有找到，就是出现查找失败的情况，就相当于找到了要插入的位置。我们可以修改，只要多加一条if判断语句，当查找到键值时输出“二叉树中有此节点了！”，如果找不到，再将此节点加到此二叉树中。算法如下所示。

	btree ptr=NULL;
if((search(ptr,data))!=NULL)     //查找二叉树
    cout<<"二叉树中有此节点了-"<<data<<endl;
else
	{
    	ptr=creat_tree(ptr,data);//将此键值加入到此二叉树中
    	inorder(ptr);
	}

btree creat_tree(btree root,int val)
{  
	btree newnode,current,backup;
	newnode=(btree)malloc(sizeof(node));//创建一个新结点
	newnode->data=val;
	newnode->left=NULL;
	newnode->right=NULL;
	if(root==NULL)    //如果树根为空
	{  
		root=newnode;
		return root;
	}
	else     //树不为空
	{  
		for(current=root;current!=NULL;)   //把树赋给root
		{  
			backup=current;    //current赋给backup
			if(current->data > val)    //val小于此结点的data
				current=current->left; //current被赋为右树的节点
			else
				current=current->right;//current被赋为左树的节点
		}
		if(backup->data >val) //节点数据域大于val值说明新结点是它的左孩子
			backup->left=newnode;
		else
			backup->right=newnode;
	}
	return root;
}

}
void inorder(btree ptr)			//中序遍历子程序
{  
  if(ptr!=NULL)
     {  
      inorder(ptr->left);
      cout<<"["<<ptr->data<<"]";
      inorder(ptr->right);
      }
}

二叉树的删除

1.删除的结点为树叶：只要将其相连的父节点指向NULL即可。

2.删除的节点只有一颗子树，如下图，要删除节点1，就要将其右指针放到其父节点的左指针

3.删除的节有两颗子树，如下图，要删除节点4，方式有两种

3.1 找出中序立即先行者（inorder immediate predecessor）

即是将欲删除节点的左子树中最大者向上提，在此即为图中的节点2，简单来说，就是在该节点的左子树，往右寻找，直到右指针为NULL，这个节点就是中序立即先行者。

3.2 找出中序立即后继者（inorder immediate successor）

即是将欲删除节点的右子树中最小者向上提，在此即为图中的节点5，简单来说，就是在该节点的右子树，往左寻找，直到左指针为NULL，这个节点就是中序立即后继者。

平衡二叉树（AVL树）

由于二叉查找树的缺点是无法永远保持在最佳状态。当加入的数据部分已排序的情况下，极有可能产生斜二叉树，因而使树的高度增加，导致查找效率降低。所以二叉查找树不利于数据的经常变动（加入或删除）的情况。为了能够尽量降低所需要的时间，在查找的时候能够很快找到所要的键值，就必须让树的高度越小越好。

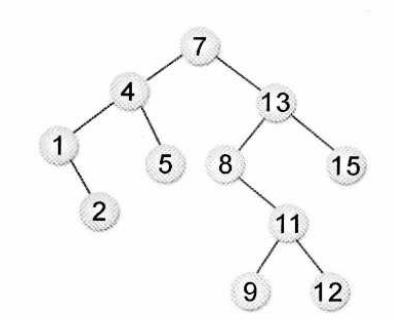
现在又a[8] = {1,2,3,4,5,6,7,8}需要构建二叉排序树。在没有学习平衡二叉树之前，根据二叉排序树的特性，通常会将它构建成如下左图。虽然完全符合二叉排序树的定义，但是对这样高度达到8的二叉树来说，查找是非常不利的。因此，更加期望构建出如下右图的样子，高度为4的二叉排序树，这样才可以提供高效的查找效率。
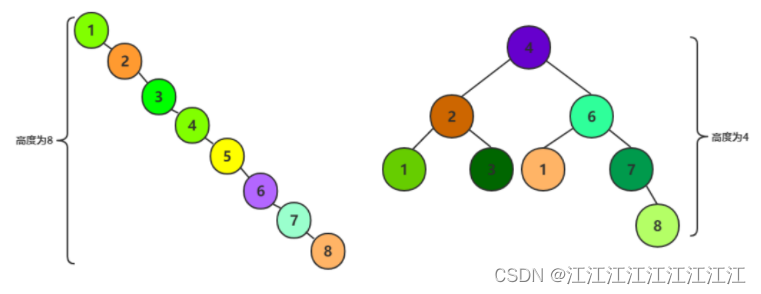
在这里插入图片描述

二叉排序树

由序列{1，2，3，4，5}得到二叉排序树：ASL=（1+2+3+4+5）/5=3

由序列{3，1，2，5，4}得到二叉排序树：ASL =（2+3+1+3+2）/5= 2.2

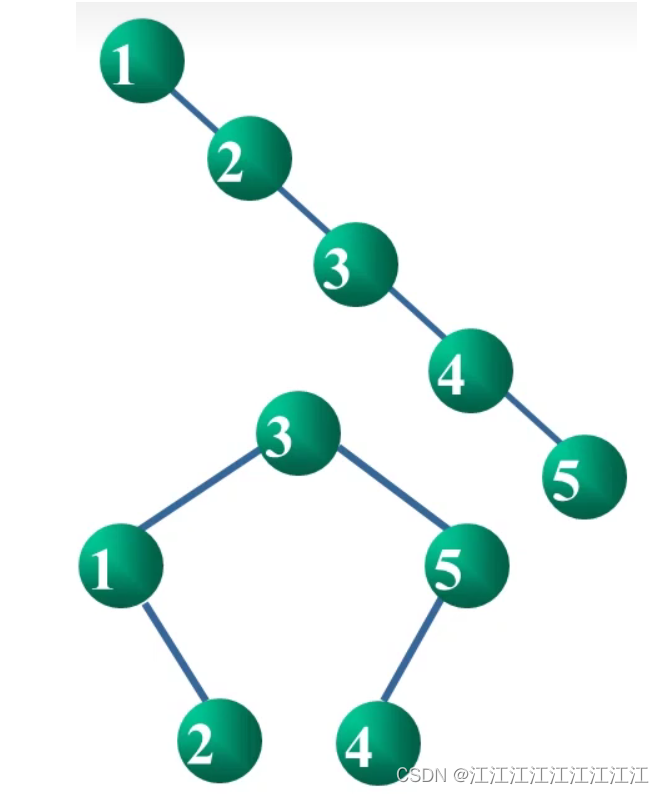
在这里插入图片描述

平衡树的定义

在AVL树中，每次在插入数据和删除数据后，必要的时候会对二叉树作一些高度的调整让二叉查找树的高度随时维持平衡。T是一个非空的二叉树， $T_l$ 和 $T_r$ ，分别是它的左右子树，若符合 $\left|h_{1}-h_{r}\right|\leq1$ 。 $h_i$ 和 $h_r$ ，分别为 $T_l$ 和 $T_r$ 的高度，也就是所有内部节点的左右子树高度相差必定小于或等于1，则称T是个高度平衡树。

平衡因子：结点的平衡因子是该结点的左子树的深度与右子树的深度之差。

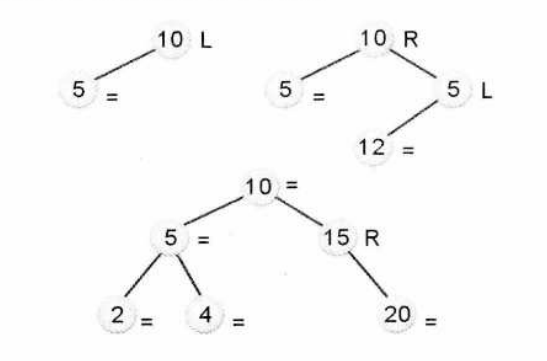
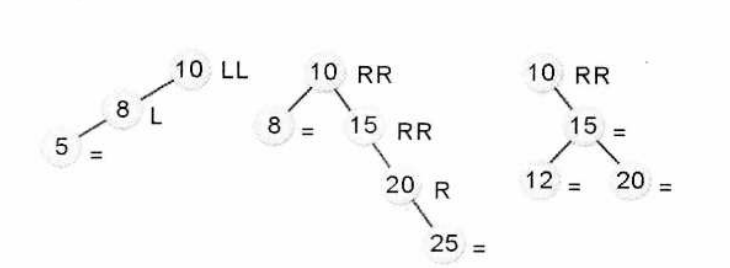
平衡二叉树的调整

构造平衡二叉树的基本思想：每插入一个结点，
（1）从插入结点开始向上计算各结点的平衡因子，如果某结点平衡因子的绝对值超过1，则说明插入操作破坏了二叉排序树的平衡性，需要进行平衡调整；否则继续执行插入操作。
（2）如果二叉排序树不平衡，则找出最小不平衡子树的根结点，根据新插入结点与最小不平衡子树根结点之间的关系判断调整类型。
（3）根据调整类型进行相应的调整，使之成为新的平衡子树。

当我们从零开始插入一个二叉树的时候，最开始是一个空的树

if (root == NULL) {
		root = (AVLTREE*)malloc(sizeof(AVLTREE));
		root->data = data;
		root->height = 0;
		root->leftChlid = root->rightChild = NULL;
	}

如果判断树为空，那么我们先给树跟分配一个空间，树的data域储存第一个数据，这个树的高度为零，左右孩子都为空。

然后当我们去插入节点的时候，通过规则判断，比这个数据小的会储存到左孩子中，比这个数据大的会储存到右孩子中。但当我们插入第三个开始就可能会出现不平衡的情况，即不符合 $\left|h_{1}-h_{r}\right|\leq1$ 我们归纳为以下四种情况，每次插入我们都进行判断，从而保证二叉树一直在一个平衡的状态。

设结点A为最小不平衡子树的根结点，对该子树进行平衡调整归纳起来有以下四种情况：
1.LL型

RR型
LR型
RL型

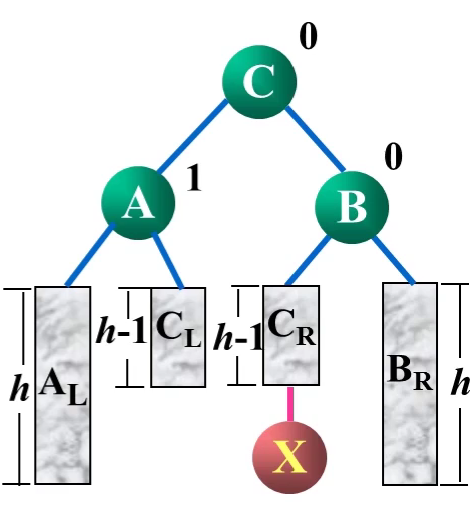
LL型

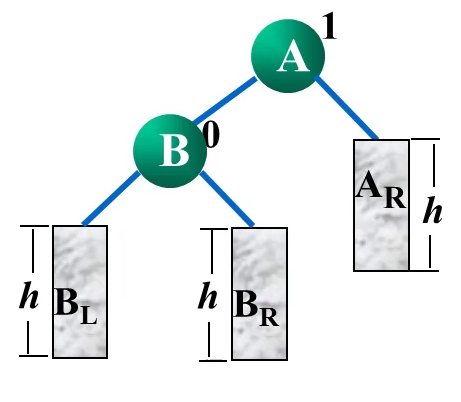
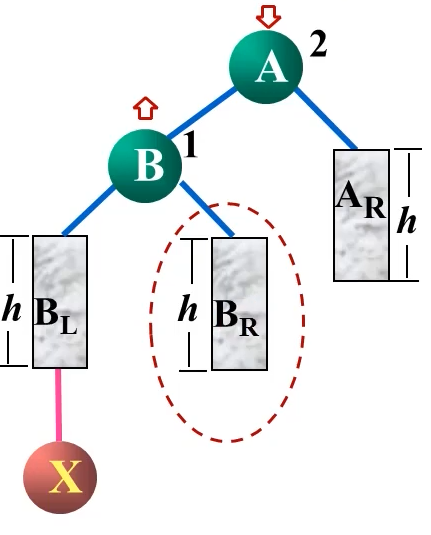
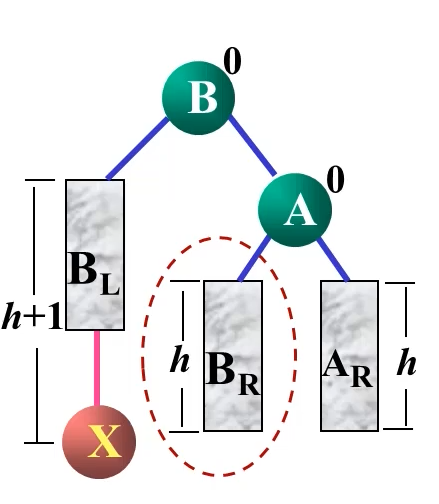
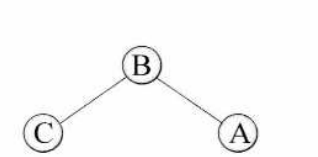
当根结点左子树的左子树中的节点导致根结点的平衡因子为2时，采用LL型旋转进行调整。

因为我们插入的时候就已经知道 $B_R$ 是大于B小于A的，所以我们可以把 $B_R$ 当作A的一个左孩子

 if (data < root->data) {    //如果要插入的数据小于树的data域，插入为树的左孩子            
		root->leftChlid = insertPoint(data, root->leftChlid); 

		if (getHeight(root->leftChlid) - getHeight(root->rightChild) == 2) {//如果左子树的深                                                                          度比右子树的深度高1
			if (data < root->leftChlid->data)  //插入数据小于左孩子就是左左
				root = left_Left_Rotation(root);
			else                               //反之则为右右
				root = left_Right_Rotation(root);
		}
	}

左左的操作

AVLTREE* left_Left_Rotation(AVLTREE* root) {
	AVLTREE* newRoot = NULL;

	newRoot = root->leftChlid;
	root->leftChlid = newRoot->rightChild;
	newRoot->rightChild = root;

	root->height = max(getHeight(root->leftChlid), getHeight(root->rightChild)) + 1;
	newRoot->height = max(getHeight(newRoot->leftChlid), root->height) + 1;

	return newRoot;
}

RR型

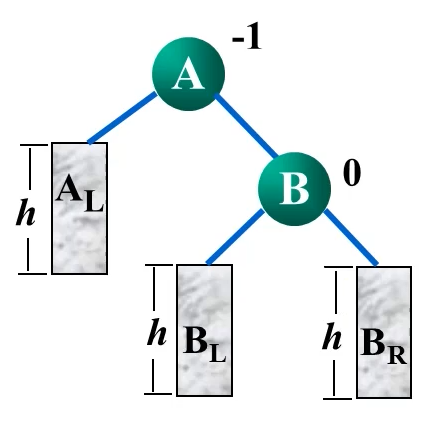
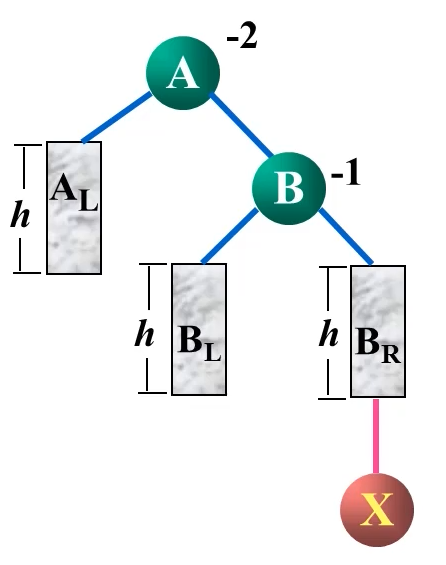
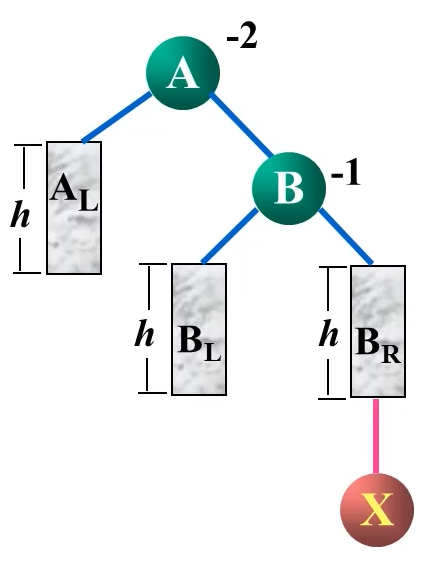
AVLTREE* right_Right_Rotation(AVLTREE* root) {
	AVLTREE* newRoot = NULL;

	newRoot = root->rightChild;
	root->rightChild = newRoot->leftChlid;
	newRoot->leftChlid = root;

	root->height = max(getHeight(root->leftChlid), getHeight(root->rightChild)) + 1;
	newRoot->height = max(getHeight(newRoot->rightChild), root->height) + 1;

	return newRoot;
}

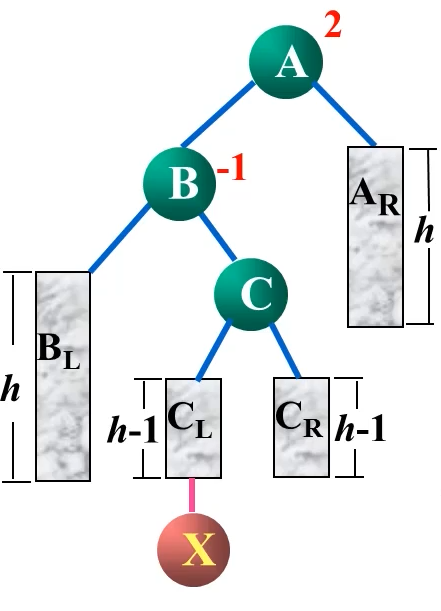
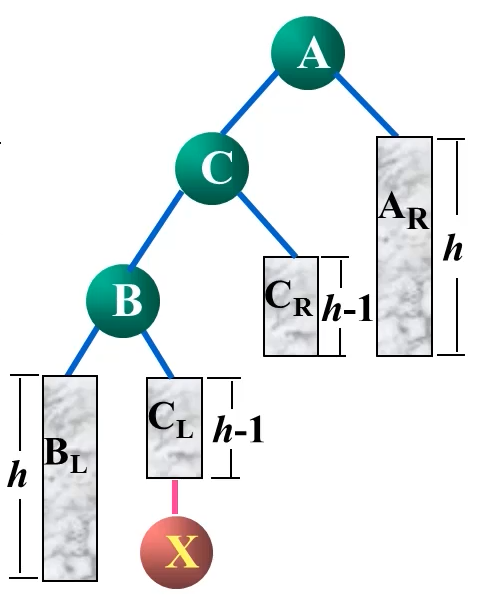
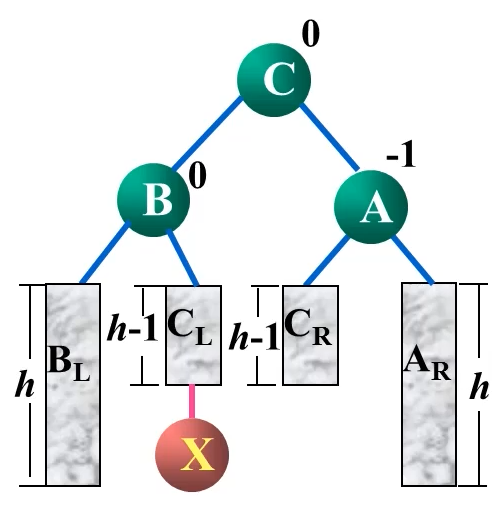
LR型

LR型是一种特殊情况，前面两次LL和RR都是单旋转，而LR型和RL型是双旋转

对其应该先进行一次右右，再进行一次左左

AVLTREE* left_Right_Rotation(AVLTREE* root) {
	root->leftChlid = right_Right_Rotation(root->leftChlid);

	return left_Left_Rotation(root);
}

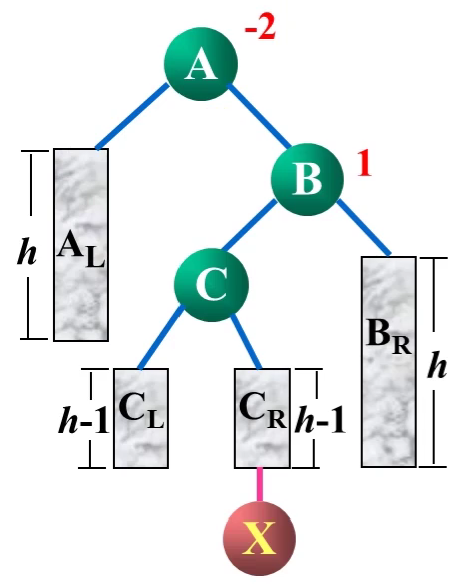
RL形

AVLTREE* right_Left_Rotation(AVLTREE* root) {
	root->rightChild = left_Left_Rotation(root->rightChild);

	return right_Right_Rotation(root);
}

AVL树的插入

AVLTREE* insertPoint(int data, AVLTREE* root) {
	
	if(root == NULL) {
		root = (AVLTREE *)malloc(sizeof(AVLTREE));
		root->data = data;
		root->height = 0;
		root->leftChlid = root->rightChild = NULL;
	} else if(data < root->data) { //如果插入数据小于树的数据，则插入到书的左子树        
		root->leftChlid = insertPoint(data, root->leftChlid);
		
		if(getHeight(root->leftChlid) - getHeight(root->rightChild) == 2) {	//判断是LX
			if(data < root->leftChlid->data)
				root = left_Left_Rotation(root);//判断为LL
			else
				root = left_Right_Rotation(root);//判断为LR
		}
	} else if(data > root->data) {//如果插入数据大于于树的数据，则插入到书的左子树  
		root->rightChild = insertPoint(data, root->rightChild);
		if(getHeight(root->rightChild) - getHeight(root->leftChlid) == 2) {//判断为RX型
			if(data > root->rightChild->data)  //判断为RR型
				root = right_Right_Rotation(root);
			else                               //判断为RL型
				root = right_Left_Rotation(root);
		}
	} else if(data == root->data) {
		return NULL;               
	}
 
	root->height = max(getHeight(root->leftChlid), getHeight(root->rightChild)) + 1;
	return root;
}

平衡二叉树的删除

删除操作和二叉查找树删除一样，分为三种情况讨论

（1）删除节点没有左右子树，这种情况直接删除此节点即可

（2）删除节点没有左子树，这种情况直接将删除节点的父节点指向删除节点的右子树。

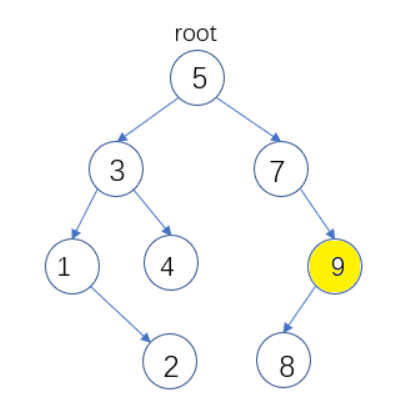
（3）删除节点没有右子树，这种情况直接将删除节点的父节点指向删除节点的左子树。

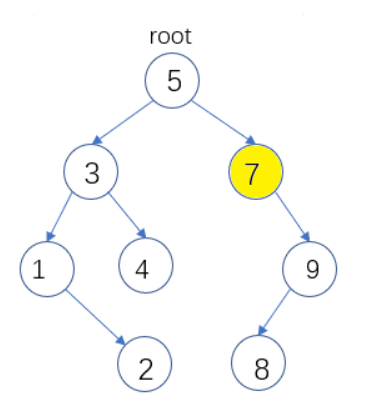
（4）删除节点左右子树都存在，可以采用两种方式，

1：让删除节点左子树的最右侧节点代替当前节点

2：让删除节点右子树的最左侧节点代替当前节点

只有左右子树，或者无子树

	AVLTREE* temp = root;

	root = root->leftChlid ? root->leftChlid : root->rightChild;
	destroy(temp);

创建一个临时节点存放树，如果左孩子不为空，此节点root等于root的左子树，如果左子树节点为空，此节点root就等于root的右孩子。就相当于删除了root

如果是没有子节点的情况下，三目运算判断root为root的右子树，但是右子树为null就相当于把其删去

有左右子树

if (root->leftChlid && root->rightChild) {

			if (getHeight(root->leftChlid) > getHeight(root->rightChild)) {
				
				AVLTREE* max = getMaxNum(root->leftChlid);
				root->data = max->data;
				root->leftChlid = deletePoint(max->data, root->leftChlid);
			}
			else {
				
				AVLTREE* min = getMinNum(root->rightChild);
				root->data = min->data;
				root->rightChild = deletePoint(min->data, root->rightChild);
			}
		}

重要的是，在每一次删除节点以后，都要对新的树进行判断是否平衡，也就是平衡因子是小于等于1。

待删除的点在左子树

if (abs(getHeight(root->rightChild) - getHeight(root->leftChlid)) == 2) {
			AVLTREE* p = root->rightChild;

			if (getHeight(p->leftChlid) > getHeight(p->rightChild)) {
				root = right_Left_Rotation(root);
			}
			else {
				root = right_Right_Rotation(root);
			}
		}

待删除的点在右子树

if (abs(getHeight(root->leftChlid) - getHeight(root->rightChild)) == 2) {
			AVLTREE* p = root->leftChlid;
			if (getHeight(p->rightChild) > getHeight(p->leftChlid)) {
				root = left_Right_Rotation(root);
			}
			else {
				root = left_Left_Rotation(root);
			}

输入

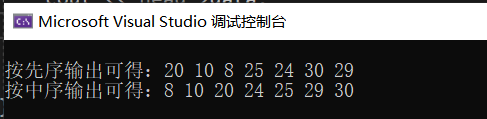
20 10 25 8 24 30 29

运行结果

先序和中序遍历

删除

删除24

运行结果

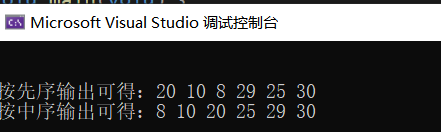
源代码

#include<iostream>
#include<malloc.h>
#include<math.h>
using namespace std;


typedef struct AVLTREE {
	int data;
	int height;
	struct AVLTREE* leftChlid;
	struct AVLTREE* rightChild;
}AVLTREE;

typedef unsigned char boolean;
#define TRUE            1  
#define FALSE           0  

static int i = 1;

void showBtreeByLeft(AVLTREE* head);
void showBtreeByMid(AVLTREE* head);
AVLTREE* left_Left_Rotation(AVLTREE* root);
AVLTREE* right_Right_Rotation(AVLTREE* root);
AVLTREE* left_Right_Rotation(AVLTREE* root);
AVLTREE* right_Left_Rotation(AVLTREE* root);
AVLTREE* insertPoint(int data, AVLTREE* root);
AVLTREE* deletePoint(int data, AVLTREE* root);
int getHeight(AVLTREE* root);
int max(int data1, int data2);
AVLTREE* getMaxNum(AVLTREE* root);
AVLTREE* getMinNum(AVLTREE* root);
void destroy(AVLTREE* root);

void destroy(AVLTREE* root) {
	if (root == NULL) {
		return;//如果树为空就不用处理
	}

	root->leftChlid = NULL;//如果树的左孩子跟右孩子都是零，那么就让整个树为空
	root->rightChild = NULL;
	root = NULL;
}

AVLTREE* getMinNum(AVLTREE* root) {
	if (root == NULL) {
		return NULL;
	}

	while (root->leftChlid != NULL) {//如果左孩子为空就停止，此时返回最小树
		root = root->leftChlid;
	}
	return root;
}

AVLTREE* getMaxNum(AVLTREE* root) {
	if (root == NULL) {
		return NULL;
	}

	while (root->rightChild != NULL) {//找到最大的数值
		root = root->rightChild;
	}
	return root;
}

int max(int data1, int data2) {
	return ((data1 > data2) ? data1 : data2);
}

int getHeight(AVLTREE* root) {
	if (root == NULL)       //得到一个树的树高
		return -1;
	else
		return root->height;
}

AVLTREE* deletePoint(int data, AVLTREE* root) {
	// 根为空 或者 没有要删除的节点，直接返回NULL
	if (root == NULL || data == NULL) {
		return NULL;
	}

	// 待删除的节点在root的左子树
	if (data < root->data) {
		root->leftChlid = deletePoint(data, root->leftChlid);
		// 删除节点后，若AVL树失去平衡，则进行相应的调节
		if (abs(getHeight(root->rightChild) - getHeight(root->leftChlid)) == 2) {
			AVLTREE* p = root->rightChild;

			if (getHeight(p->leftChlid) > getHeight(p->rightChild)) {
				root = right_Left_Rotation(root);
			}
			else {
				root = right_Right_Rotation(root);
			}
		}
		// 待删除的节点在root的右子树
	}
	else if (data > root->data) {
		root->rightChild = deletePoint(data, root->rightChild);
		// 删除节点后，若AVL树失去平衡，则进行相应的调节
		if (abs(getHeight(root->leftChlid) - getHeight(root->rightChild)) == 2) {
			AVLTREE* p = root->leftChlid;
			if (getHeight(p->rightChild) > getHeight(p->leftChlid)) {
				root = left_Right_Rotation(root);
			}
			else {
				root = left_Left_Rotation(root);
			}
		}
		// root就是要删除的节点
	}
	else if (data == root->data) {
		//左右孩子非空
		if (root->leftChlid && root->rightChild) {

			if (getHeight(root->leftChlid) > getHeight(root->rightChild)) {
				// 如果root的左子树比右子树高；
				// 则找出root的左子树中的最大节点
				//   将该最大节点的值赋值给root
				//   删除该最大节点
				// 这类似于用root的左子树中最大节点做root的替身
				// 删除root的左子树中最大节点之后，AVL树仍然是平衡的
				AVLTREE* max = getMaxNum(root->leftChlid);
				root->data = max->data;
				root->leftChlid = deletePoint(max->data, root->leftChlid);
			}
			else {
				// 如果root的左子树比右子树低；
				// 则找出root的左子树中的最小节点
				//   将该最小节点的值赋值给root
				//   删除该最小节点
				// 这类似于用root的右子树中最小节点做root的替身
				// 删除root的左子树中最小节点之后，AVL树仍然是平衡的
				AVLTREE* min = getMinNum(root->rightChild);
				root->data = min->data;
				root->rightChild = deletePoint(min->data, root->rightChild);
			}
		}

		else {
			//这种情况为左孩子为空右孩子不为空、或者右孩子为空左孩子不为空、左右孩子都为空时的处理方法
			//直接通过一个三目运算，即可完美解决
			AVLTREE* temp = root;

			root = root->leftChlid ? root->leftChlid : root->rightChild;

			destroy(temp);
		}
	}

	return root;
}
/*
		如果节点为空，那么创建一个节点
		下面也分别给出了当要插入的节点大于或小于或等于当前节点的情况
		当一个节点的左右孩子高度差为2时，说明树需要旋转
		至于是单旋转还是双旋转,得看插入的位置是左子树还是右子树
		然后根据相应结构，选择单旋转或者双旋转
*/
AVLTREE* insertPoint(int data, AVLTREE* root) {

	if (root == NULL) {
		root = (AVLTREE*)malloc(sizeof(AVLTREE));
		root->data = data;
		root->height = 0;
		root->leftChlid = root->rightChild = NULL;
	}
	else if (data < root->data) {
		root->leftChlid = insertPoint(data, root->leftChlid);

		if (getHeight(root->leftChlid) - getHeight(root->rightChild) == 2) {
			if (data < root->leftChlid->data)
				root = left_Left_Rotation(root);
			else
				root = left_Right_Rotation(root);
		}
	}
	else if (data > root->data) {
		root->rightChild = insertPoint(data, root->rightChild);
		if (getHeight(root->rightChild) - getHeight(root->leftChlid) == 2) {
			if (data > root->rightChild->data)
				root = right_Right_Rotation(root);
			else
				root = right_Left_Rotation(root);
		}
	}
	else if (data == root->data) {
		return NULL;
	}

	root->height = max(getHeight(root->leftChlid), getHeight(root->rightChild)) + 1;
	return root;
}

AVLTREE* right_Left_Rotation(AVLTREE* root) {
	root->rightChild = left_Left_Rotation(root->rightChild);

	return right_Right_Rotation(root);
}

AVLTREE* left_Right_Rotation(AVLTREE* root) {
	root->leftChlid = right_Right_Rotation(root->leftChlid);

	return left_Left_Rotation(root);
}

AVLTREE* right_Right_Rotation(AVLTREE* root) {
	AVLTREE* newRoot = NULL;

	newRoot = root->rightChild;
	root->rightChild = newRoot->leftChlid;
	newRoot->leftChlid = root;

	root->height = max(getHeight(root->leftChlid), getHeight(root->rightChild)) + 1;
	newRoot->height = max(getHeight(newRoot->rightChild), root->height) + 1;

	return newRoot;
}

AVLTREE* left_Left_Rotation(AVLTREE* root) {
	AVLTREE* newRoot = NULL;

	newRoot = root->leftChlid;
	root->leftChlid = newRoot->rightChild;
	newRoot->rightChild = root;

	root->height = max(getHeight(root->leftChlid), getHeight(root->rightChild)) + 1;
	newRoot->height = max(getHeight(newRoot->leftChlid), root->height) + 1;

	return newRoot;
}

void showBtreeByMid(AVLTREE* head) {
	if (head == NULL) {
		return;
	}
	showBtreeByMid(head->leftChlid);
	cout << head->data;
	cout << " ";
	showBtreeByMid(head->rightChild);
}

void showBtreeByLeft(AVLTREE* head) {
	if (head == NULL) {
		return;
	}

	cout << head->data;
	cout << " ";
	showBtreeByLeft(head->leftChlid);
	showBtreeByLeft(head->rightChild);
}

void main(void) {
	AVLTREE* root = NULL;
	root = insertPoint(20, root);
	root = insertPoint(10, root);
	root = insertPoint(25, root);
	root = insertPoint(8, root);
	root = insertPoint(24, root);
	root = insertPoint(30, root);
	root = insertPoint(29, root);
	cout << endl;
	cout << "按先序输出可得：";
	showBtreeByLeft(root);
	cout << endl;
	cout << "按中序输出可得：";
	showBtreeByMid(root);
	cout << endl;
	root = deletePoint(24, root);
	cout << endl;
	cout << "按先序输出可得：";
	showBtreeByLeft(root);
	cout << endl;
	cout << "按中序输出可得：";
	showBtreeByMid(root);
	cout << endl;
}

作业四-----最短路径（Dijsktra）

图的定义

图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：
$G = (V, E)$
其中：G表示一个图，V是图G中顶点的集合，E是图G中顶点之间边的集合。

在线性表中，元素个数可以为零，称为空表；

在树中，结点个数可以为零，称为空树；

在图中，顶点个数不能为零，但可以没有边。(没有空图的概念)

不同逻辑结构关系的对比

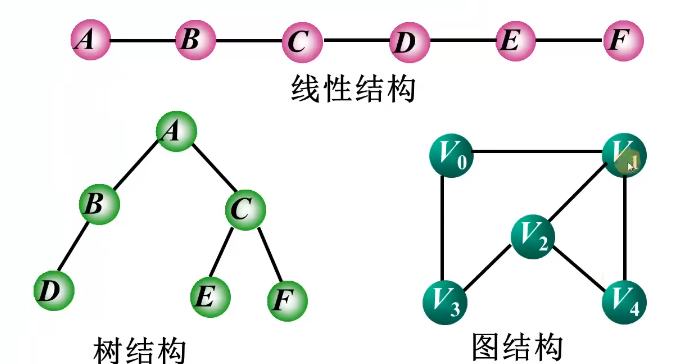
在线性结构中，数据元素之间仅具有线性关系；
在树结构中，结点之间具有层次关系；
在图结构中，任意两个顶点之间都可能有关系。

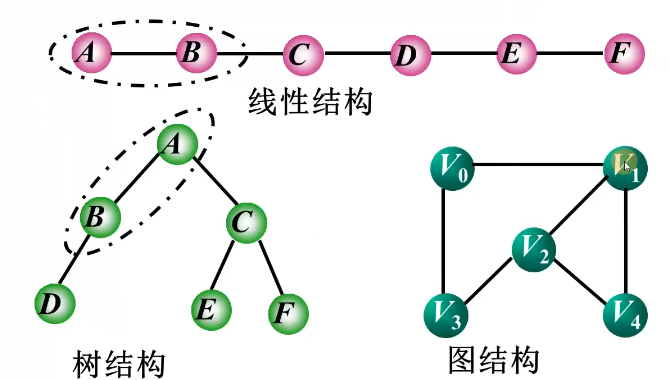
在线性结构中，元素之间的关系为前驱和后继
在树结构中，结点之间的关系为双亲和孩子
在图结构中，顶点之间的关系为邻接。

图的储存

图的粗存结构及实现

邻接矩阵

基本思想：用一个一维数组存储图中顶点的信息，用一个二维数组（称为邻接矩阵）存储图中各顶点之间的邻接关系。

无向图的邻接矩阵

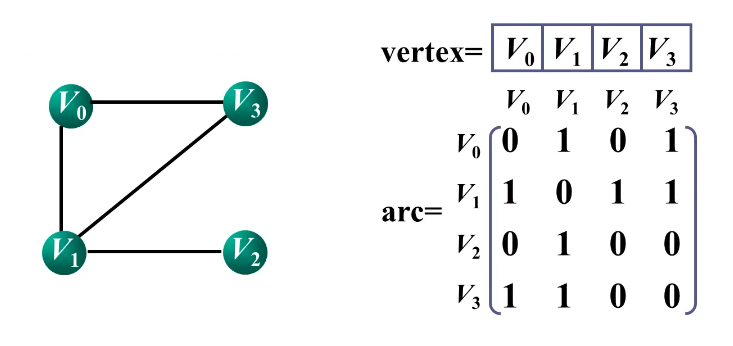
网图邻接矩阵的定义

$\textbf{arc}[i][j]=\left\{\begin{array}{l}\boldsymbol{w}_{ij}，若(v_i,v_j)\in E(或<v_i,v_j>\in E) \\ \boldsymbol{0},若i=j \\{\infty}，其他\end{array}\right.$

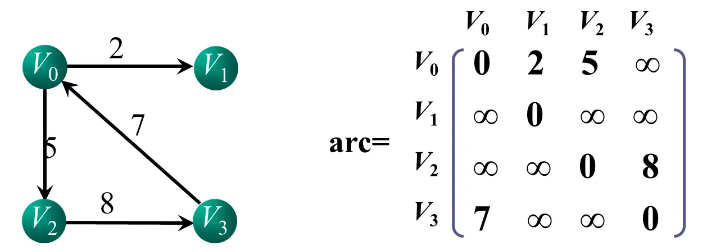
图的储存结构及实现

const int MAX_VERTEX=10;//图的最大顶点数
class MGraph{
	private:
		Data Type vertex[MAX_VERTEX];  
		int arc[MAX_VERTEX][MAX_VERTEX];
		int vertexNum， arcNum；
	public：
		MGraph(DataType v[]，int n，int e);//构造函数
		-MGraph();           //析构函数
		void DFSTraverse(int v); //深度遍历
		void BFSTrayerse(int v);  //广度遍历
}；

构造函数的实现

邻接矩阵中图的基本操作——构造函数
1.确定图的顶点个数和边的个数；
2.输入顶点信息存储在一维数组vertex中；
3.初始化邻接矩阵arc；
4.依次输入每条边存储在邻接矩阵arc中；
4.1输入边依附的两个顶点的序号i，j；
4.2将邻接矩阵的第i行第j列的元素值置为1；
4.3将邻接矩阵的第j行第i列的元素值置为1；

MGraph::MGraph（Data Type v[], int n,int e）{
	vertexNum = n;
	arcNum = e;
	for （i = 0; i < vertexNum; i++）
		vertex[i] = v[i];
	for （i = 0; i < vertexNum; i++）
	//初始化邻接矩阵
		for （j = 0; j < vertexNum; j++）
			arc[i][] = 0;
	for （i = 0; i< arcNum; i++）[ //依次输入每一条边
		cin >>vi>>vj； //输入边依附的两个顶点的编号
		arc[vi][vj] = 1; //置有边标志
		arc[vj][vi] = 1;
     }
   }

邻接表

图的邻接矩阵储存结构的空间复杂度？

假设图G有n个顶点e条边，则储存该图需要 $O(n^2)$

如果为稀疏图则会出现什么现象？

邻接表储存的基本思想：对于图的每个顶点 $v_i$ ，将所有邻接于 $v_i$ 的顶点链成一个单链表，称为顶点 $v_i$ 的边表（对于有向图则称为出边表）所有边表的头指针和存储顶点信息的一维数组构成了顶点表。

vertex	数据域，存放顶点信息
firstEdge	指针域，指向边表中第一个结点
adjvex	邻接点域，边的终点在顶点表中的下标
next	指针域，指向边表中的下一个结点

struct ArcNode//边表
{
	int adjvex;
	ArcNode *next;
};
struct VertexNode //顶点表
{
	DataType vertex;
	ArcNode *fristEdge;
};

图的存储结构及实现

邻接表存储有向图的类

const int MAx_VERTEX = 10;
class ALGraph{
	private:
		VertexNode adjList[MAX_VERTEX];
		int vertexNum,arcNum;
	public:
		ALGraph(DataType v[],int n,int e);//构造函数
		~ALGraph();                      //析构函数
		void DFSTraverse(int v);
		void BFSTraverse(int v);
}

邻接表中图的基本操作----构造函数

1.确定图的顶点个数和边的个数

2.输入顶点信息，初始化该顶点的边表

3.依次输入边的信息并储存在边表中

3.1输入边所依附的两个顶点的序号 $v_i$ 和 $v_j$

3.2生成邻接点序号为 $v_j$ 的边表结点s

3.3将结点s插入到第 $v_i$ 个边表的头部

ALGraph:: ALGraph(DataType v[], int n, int e){
	vertexNum = n;
	arcNum = e;
	for (i = 0; i < vertexNum; i++) {
	//初始化顶点信息，指针域都为空
		adjList[i].vertex = v[i];
		adjList[i].firstEdge = NULL;
	}
    for(i = 0;i < arcNum ;i++){
        //输入边的信息存储在边表中
        cin>>vi>>vj;//输入边依附的两个顶点的编号
        s = newArcNode;
        s->adjvex = vj;
        s->next = adjList[vi].fristEdge;
        adjList[vi].fristEdge = s;
    }
}

图的遍历

1.在图中，任何两个顶点之间都可能存在边，顶点是没有确定的先后次序的，所以，顶点的编号不唯一。
为了定义操作的方便，将图中的顶点按任意顺序排列起来，比如，按顶点的存储顺序。

2.从某个起点始可能到达不了所有其它顶点，怎么办？

解决方案：多次调用从某顶点出发遍历图的算法。

3.因图中可能存在回路，某些顶点可能会被重复访问，那么如何避免遍历不会因回路而陷入死循环。

解决方案：附设访问标志数组visited[n]

4.在图中，一个顶点可以和其它多个顶点相连，当这样的顶点访问过后，如何选取下一个要访问的顶点？

深度和广度优先遍历

深度优先遍历

（1）访问顶点v；
（2）从v的未被访问的邻接点中选取一个顶点w，从w出发进行深度优先遍历；
（3）重复上述两步，直至图中所有和v有路径相通的顶点都被访问到。

思路

1.访问顶点v；visited[v]= 1；
2.w=顶点v的第一个邻接点；
3.while（w存在）
3.1 if（w未被访问）从顶点w出发递归执行该算法；
3.2 w=顶点v的下一个邻接点；

邻接表实现

void ALGraph::DFSTraverse(int * visited) {
	
	int i;
	for (i = 0; i < vertexNum; i++) {
		visited[i] = 0;
	}
	for (i = 0; i < vertexNum; i++) {  //循环遍历每个顶点
		if (!visited[i]) {
			DFS(i, visited);
		}
	}
}

void ALGraph::DFS(int v, int *visited) {   //遍历单个头顶点

	visited[v] = 1;
	cout << adjList[v].vertex << " ";
	ArcNode *p = adjList[v].firstEdge;
	while (p) {
		if (!visited[p->adjvex]) {
			DFS(p->adjvex, visited);
		}
		p = p->next;
	}

}

邻接矩阵实现

template<class T>
void MGraph<T>::DFS(int i,int * visited){
	cout<<vertex[i]<<" ";
	visited[i] = 1;
	for(int j=0;j<vertexNum;j++){
		if(visited[j] == 0&&arc[i][j] != 0 &&arc[i][j] != INFINIT){
			DFS(j,visited);
		}
	}
}

template<class T>
void MGraph<T>::DFSTraverse(int * visited){
	for(int i=0;i<vertexNum;i++){
		visited[i] = 0;
	}
	for(int i=0;i<vertexNum;i++){
		if(!visited[i]){
			DFS(i,visited);
		}
	}
}

广度优先遍历

基本思想：
（1）访问顶点v；
（2）依次访问v的各个未被访问的邻接点v1，V2，…，Vk
（3）分别从v1，V2,…, Vk出发依次访问它们未被访问的邻接点，并使“先被访问顶点的邻接点”先于后被访问顶点的邻接点”被访问。直至图中所有与顶点v有路径相通的顶点都被访问到。

邻接表实现

void ALGraph::BFSTraverse(int * visited) {
	
	int i;
	for (i = 0; i < vertexNum; i++) {
		visited[i] = 0;
	}
	for (i = 0; i < vertexNum; i++) {
		if (!visited[i]) {
			BFS(i, visited);
		}
	}
}

void ALGraph::BFS(int i, int *visited) {
	queue<int> q;
	visited[i] = 1;
	q.push(i);
	
	while(!q.empty()){
		int temp = q.front();
		cout<<adjList[temp].vertex<<" ";
		q.pop();
		ArcNode * p = adjList[i].firstEdge;
		while(p){
			if(!visited[p->adjvex]){
				q.push(p->adjvex);
				visited[p->adjvex] = 1;
			}
			p = p->next;
		}
	}
	
}

邻接矩阵实现

template<class T>
void MGraph<T>::BFS(int i,int * visited){
	queue<int> q;
	visited[i] = 1;
	q.push(i);
	while(!q.empty()){
		int temp = q.front();
		cout<<vertex[temp]<<" ";
		q.pop();
		for(int j=0;j<vertexNum;j++){
			if(!vertex[i]&&arc[i][j]!=0&&arc[i][j]!=INFINIT){
				
				visited[j] = 1;
				q.push(j);
			}
		}

	}
	cout<<endl;
}
template<class T>
void MGraph<T>::BFSTraverse(int * visited){
	for(int i=0;i<vertexNum;i++){
		visited[i] = 0;
	}
	for(int i=0;i<vertexNum;i++){
		if(!visited[i]){
			BFS(i,visited);
		}
	}
}

最短路径（Dijkstra算法）

在网图中，最短路径是指两顶点之间经历的边上权值之和最短的路径。

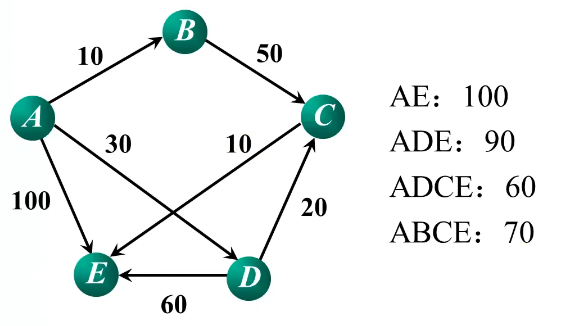
单源点最短路径问题

问题描述：给定带权有向图G=（V，E）和源点v$\in $V，求从v到G中其余各顶点的最短路径。

图的存储结构：带权的邻接矩阵存储结构

数组dist[n]：每个分量dist[i]表示当前所找到的从始点v到终点 $v_i$ ，的最短路径的长度。初态为：若从v到 $v_i$ ，有弧，则dist[i]为弧上权值；否则置dist[i]为$\infty $。数组 p a t h [n] ： p a t h [i] 是一个字符串，表示当前所找到的从始点 v 到终点$ v_i$，的最短路径。初态为：若从v到
$v_i$ 有弧，则path[i]为0；否则置path[i]为-1。
数组s[n]：存放源点和已经生成的终点，其初态为只有一个源点v。

最小生成树与最短路径的区别

最短路径问题

最短路径是求两点之间路径最短的问题，应用如导航，两个地方怎么走距离最短。可以存在到不了的情况。

这个问题是说，如何找到从某个特定的节点出发，通向其他节点的最短路径。它只着眼于点与点之间的路径问题，并不关注整个图，也就意味着对一个节点运行算法的结果与另一个节点的结果之间没有多少关系。

最小生成树问题

最小生成树是把连通的图的所有顶点连起来路径之和最小的问题，即生成树总权值之和最小。

即在一个连通的图里，如何去除图里的边，使得剩余的边仍能连接所有的节点，且这些边的权重之和最小。显然，满足这个要求的图不可能存在环，也就是一棵树，因此叫做生成树。这种算法与上面的相反，着眼于整个图的结构，并不关心某两个节点之间的路径是不是最短的。

伪代码

1.初始化数组dist、path和s；

while （s中的元素个数<n）
2.1 在dist[n]中求最小值，其下标为k；
2.2 输出dist[j]和path[jl；
2.3修改数组dist和path；
2.4将顶点 $v_k$ 添加到数组s中；

void MGraph::Dijkstra(int startV) {
	this->startV = startV;
	for (int i = 0; i < vertexNum; i++) {
		dist[i] = arc[startV][i];
		if (dist[i] != INFINIT) {
			path[i] = startV;
		}
		else {
			path[i] = -1;
		}
	}
	for (int i = 0; i < vertexNum; i++) {
		s[i] = 0;
	}
	s[startV] = 1; //startV放入s集合
	int num = 1; //s集合的元素个数为1
	while (num < vertexNum) {
		int min = findMinDist();
		//min是当前dist数组中最短路径的下标
		//前提是s[i]=0，即在s集合的补集中查找
		s[min] = 1; //min放入s集合
		for (int i = 0; i < vertexNum; i++) {
			if (s[i] == 0 && (dist[i] > dist[min] + arc[min][i])) {
				dist[i] = dist[min] + arc[min][i];
				path[i] = min;
			}
		}
		num++;
	}
	displayPath();
}

调试结果

输入

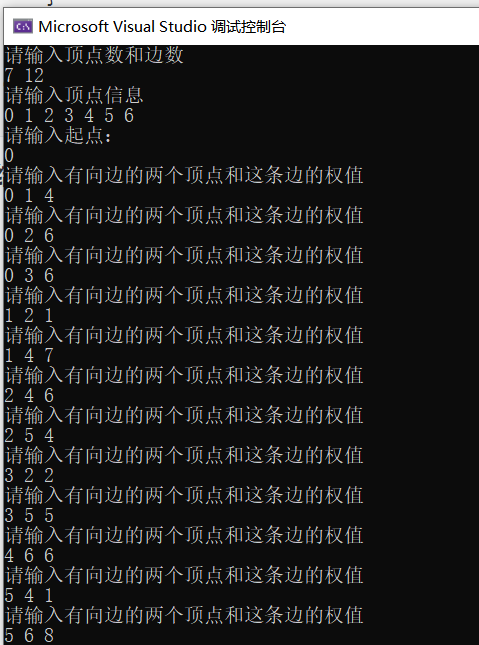
输出

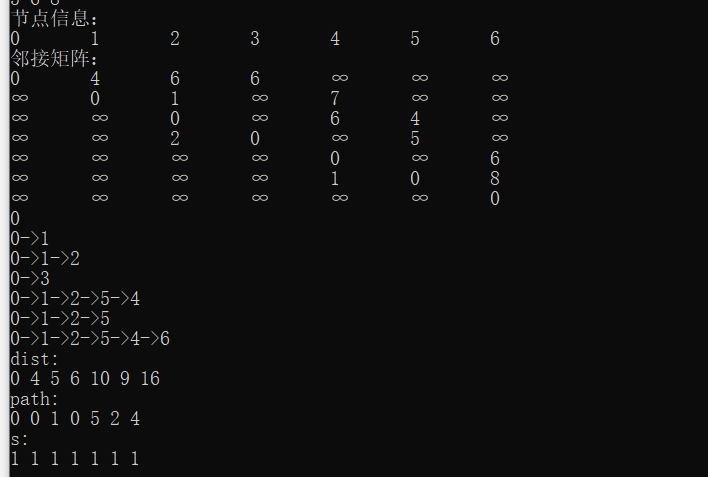
程序源码

#include<iostream>
#include<stack>
#define MAX 50
#define INFINIT 65535

using namespace std;

class MGraph {
private:
	int vertexNum, arcNum;
	int arc[MAX][MAX];
	int vertex[MAX];
	int dist[MAX];
	int path[MAX];
	int s[MAX];
	int startV;
public:
	MGraph(int v[], int n, int e);
	void display();
	void Dijkstra(int startV);
	int findMinDist();
	void displayPath();
	void displayDistPathS();
};

MGraph::MGraph(int v[], int n, int e) {
	vertexNum = n;
	arcNum = e;
	for (int i = 0; i < vertexNum; i++) {
		vertex[i] = v[i];
	}
	for (int i = 0; i < arcNum; i++) {
		for (int j = 0; j < arcNum; j++) {
			if (i == j) {
				arc[i][j] = 0;
			}
			else {
				arc[i][j] = INFINIT;
			}
		}
	}
	int vi, vj, w;
	for (int i = 0; i < arcNum; i++) {
		cout << "请输入有向边的两个顶点和这条边的权值" << endl;
		cin >> vi >> vj >> w;
		arc[vi][vj] = w; //有边标志
	}
}

void MGraph::display() {

	cout << "节点信息：" << endl;
	for (int i = 0; i < vertexNum; i++) {
		cout << vertex[i] << endl;
	}
	cout << endl;


	cout << "邻接矩阵：" << endl;
	for (int i = 0; i < vertexNum; i++) {
		for (int j = 0; j < vertexNum; j++) {
			if (arc[i][j] == INFINIT) {
				cout << "∞" << endl;
			}
			else {
				cout << arc[i][j] <<endl;
			}
		}
		cout << endl;
	}

}


void MGraph::Dijkstra(int startV) {
	this->startV = startV;
	for (int i = 0; i < vertexNum; i++) {
		dist[i] = arc[startV][i];
		if (dist[i] != INFINIT) {
			path[i] = startV;
		}
		else {
			path[i] = -1;
		}
	}
	for (int i = 0; i < vertexNum; i++) {
		s[i] = 0;
	}
	s[startV] = 1; //startV放入s集合
	int num = 1; //s集合的元素个数为1
	while (num < vertexNum) {
		int min = findMinDist();
		//min是当前dist数组中最短路径的下标
		//前提是s[i]=0，即在s集合的补集中查找
		s[min] = 1; //min放入s集合
		for (int i = 0; i < vertexNum; i++) {
			if (s[i] == 0 && (dist[i] > dist[min] + arc[min][i])) {
				dist[i] = dist[min] + arc[min][i];
				path[i] = min;
			}
		}
		num++;
	}
	displayPath();
}

int MGraph::findMinDist() {
	int minNum = INFINIT;//用于更新
	int number;
	for (int i = 0; i < vertexNum; i++) {
		if (s[i] == 0) {
			if (minNum > dist[i] && 0 != dist[i] && INFINIT != dist[i]) {
				minNum = dist[i];
				number = i;
			}
		}
	}
	return number;
}

void MGraph::displayPath() {
	for (int i = 0; i < vertexNum; i++) {
		if (i == startV) cout << i << endl;

		if (startV != i) {
			int temp = i;
			stack<int> s;
			while (temp != startV) {
				s.push(path[temp]);
				temp = path[temp];
			}
			while (!s.empty()) {
				cout << s.top() << "->";
				s.pop();
			}
			cout << i;
			cout << endl;
		}

	}
}

void MGraph::displayDistPathS() {
	cout << "dist:" << endl;
	for (int i = 0; i < vertexNum; i++) {
		cout << dist[i] << " ";
	}
	cout << endl;

	cout << "path:" << endl;
	for (int i = 0; i < vertexNum; i++) {
		cout << path[i] << " ";
	}
	cout << endl;

	cout << "s:" << endl;
	for (int i = 0; i < vertexNum; i++) {
		cout << s[i] << " ";
	}
	cout << endl;
}

int main() {
	int n, e;
	int v[MAX];
	cout << "请输入顶点数和边数" << endl;
	cin >> n >> e;
	cout << "请输入顶点信息" << endl;
	for (int i = 0; i < n; i++) {
		cin >> v[i];
	}
	cout << "请输入起点：" << endl;
	int t;
	cin >> t;
	MGraph mgraph(v, n, e);
	mgraph.display();
	mgraph.Dijkstra(t);
	mgraph.displayDistPathS();
	return 0;
}

如下图所示

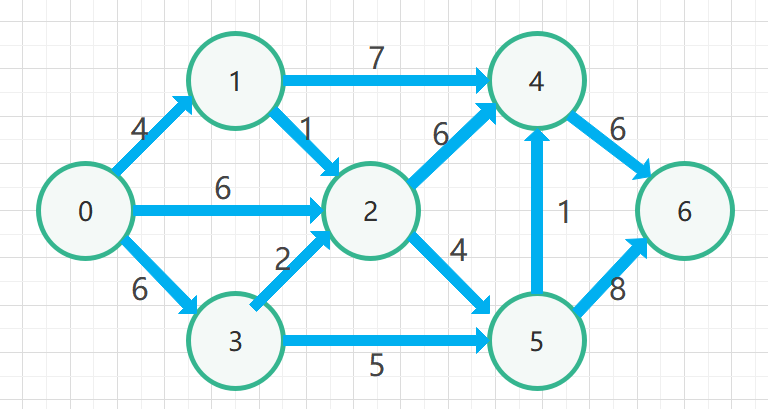
作业五------关键路径

AOE网

AOE网：在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，边上的权值表示活动的持续时间，称这样的有向图叫做边表示活动的网，简称AOE网。AOE网中没有入边的顶点称为始点（或源点），没有出边的顶点称为终点（或汇点）

AOE网的性质：

（1）只有在某顶点所代表的事件发生后，从该顶点出发的各活动才能开始；
（2）只有在进入某顶点的各活动都结束，该顶点所代表的事件才能发生

AVE网应用举例

请问汽车厂造一辆汽车，最短需要多少时间？
其中生产一个轮子：0.5天，发动机：3天，底盘：2天，外壳：2天，其他零部件：2天，全部零部件集中到一起：0.5天，组装成车并完成测试：2天。

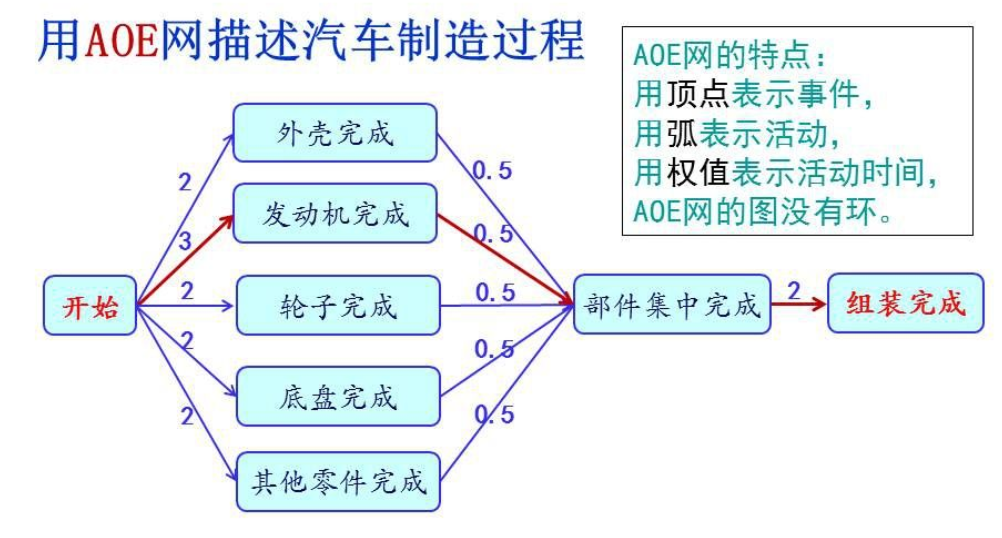
AOE网

例如，事件 $v_4$ 表示活动 $a_3$ 和 $a_4$ 已经结束，活动 $a_6$ 和 $a_7$ 可以开始。

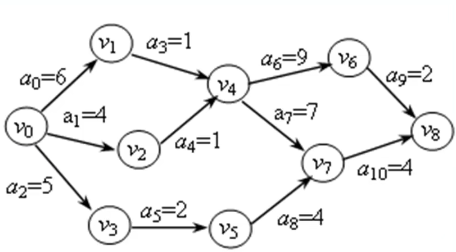
AOE网可以回答下列问题：
1.完成整个工程至少需要多少时间？
2.为缩短完成工程所需的时间，应当加快哪些活动？

关键路径

关键路径：在AOE网中，从始点到终点具有最大路径长度（该路径上的各个活动所持续的时间之和）
的路径称为关键路径。
关键活动：关键路径上的活动称为关键活动。

首先计算以下与关键活动有关的量：
（1）事件的最早发生时间ve[k]
（2）事件的最迟发生时间vl[k]
（3）活动的最早开始时间ee[i]
（4）活动的最晚开始时间el[i]
最后计算各个活动的时间余量el[k]-ee[k]，时间余
量为0者即为关键活动。

（1）事件的最早发生时间ve[k]

ve[k]是指从始点开始到顶点v的最大路径长度。这个长度决定了所有从顶点v发出的活动能够开工的最早时间。

（2）事件的最迟发生时间vl[k]

vl[k]是指在不推迟整个工期的前提下，事件v允许的最晚发生时间。

（3）活动的最早开始时间ee[i]

若活动a，是由弧< $v_k$ ， $v_j$ >表示，则活动 $a_i$ 的最早开始时间应等于事件 $v_k$ 的最早发生时间。因此：
$ee [i] = v e [k]$

（4）活动的最晚开始时间el[i]

若 $a_i$ 由弧< $v_k$ ， $v_j$ >表示，则 $a_i$ 的最晚开始时间要保证事件 $v_j$ ，的最迟发生时间不拖后。因此，有： $\mathbf{el}[\mathbf{i}]=\mathbf{vl}[\mathbf{j}]-\mathbf{len}<\mathbf{v}_k,\mathbf{v}_j>$

注意

（1）如果想缩短工程时间，可通过提高对应关键路径上的关键活动的速度来实现，但提高幅度必须适当，因为只有在不改变AOE网的关键路径的前提下，提高关键活动的速度才能有效缩短工程总时间；
（2）若AOE网中同时存在几条关键路径的话，只单独提高其中某一条关键路径上的关键活动的速度并不能提高整个工程的工作效率来缩短总工期只有同时提高这几条关键路径上的关键活动的速度才可以。

首先调用TopologicalSort函数检查是否是一个没有环的图

bool ALGraph::CriticalPath() {

	int resultStack[MAX_VERTEX]; //存储拓扑排序结果序列(存储下标)
	int resultTop;               //拓扑排序有效顶点个数(栈顶指针)
	ArcNode* p;
	int count;
	int inVex, outVex;  //inVex,outVex，分别代表一条边的起点顶点号和终点顶点号

	if (!TopologicalSort(resultStack, count)) {
		return false;
	}

	//输出拓扑排序的顶点处理顺序
	cout << "拓扑排序的顶点处理顺序是：" << endl;
	for (int i = 0; i < count; i++) {
		cout << resultStack[i] << " ";
	}
	cout << endl;


	//输出ve数组的值
	cout << "ve数组的值为：" << endl;
	for (int i = 0; i < count; i++) {
		cout << "ve[" << i << "]=" << ve[i] << endl;
	}


	//求解vl数组的值
	resultTop = count - 1;
	inVex = resultStack[resultTop--];//汇点出栈
	for (int i = 0; i < vertexNum; i++) {
		vl[i] = ve[inVex]; //用最大值初始化
	}

	//栈不为空时，按拓扑逆序求各个顶点的vl值
	while (resultTop != -1) {
		inVex = resultStack[resultTop--];
		p = adjList[inVex].firstEdge;
		while (p) {
			outVex = p->adjvex;
			if (vl[inVex] > vl[outVex] - p->weight) {
				vl[inVex] = vl[outVex] - p->weight;
			}
			p = p->next;
		}
	}
	cout << "vl数组的值为：" << endl;
	for (int i = 0; i < count; i++) {
		cout << "vl[" << i << "]=" << vl[i] << endl;
	}


	//完成关键路径的求解
	cout << "输出关键路径：" << endl;

	//从上往下扫描顶点表，处理每个顶点的边表
	for (inVex = 0; inVex < vertexNum; inVex++) {
		p = adjList[inVex].firstEdge;
		while (p) {
			outVex = p->adjvex;
			int weight = p->weight;
			int ee = ve[inVex];
			int el = vl[outVex] - weight;

			if (ee == el) {
				cout << "<" << inVex << "," << outVex << ">" << weight << " ";
			}
			p = p->next;
		}
	}
	return true;
}

程序思路

1，从源点 $v_0$ 出发，令ve[0]=0，按拓扑序列求其余各顶点的最早发生时间ve[i]；
2.如果得到的拓扑序列中顶点个数小于AOE网中的顶点数，则说明网中存在环，不能求关键路径，算法终止；否则执行步骤3；
3.从终点 $v_{n-1}$ 出发，令vl[n-1]=ve[n-1]，按逆序拓扑有序求其余各顶点的最迟发生时间vl[i]；
4.根据各顶点的ve和vl值，求每条有向边的最早开始时间ee[i]和最迟开始时间el[i]；
5，若某条有向边 $a_i$ ，满足条件ee[i]=el[i]，则 $a_i$ 为关键活动

拓扑排序

1.栈s初始化；累加器count初始化；
2.扫描顶点表，将没有前驱的顶点压栈；
3.当栈S非空时循环
3.1 $v_j$ 退出栈顶元素；输出 $v_j$ 累加器加1；
3.2将顶点 $v_j$ 的各个邻接点的入度减1；
3.3将新的入度为0的顶点入栈；

4.if （count<vertexNum）输出有回路信息；

opologicalSort用于实现拓扑排序
参数：result用来保存处理过的拓扑排序顶点；count用来保存处理过的拓扑排序顶点的个数
功能：进行拓扑排序，将找到的拓扑顶点序号存入result数组（result可以看成一个栈,count可以看成是栈顶指针）
增加的功能：用注释--------标识，在拓扑排序的同时计算ve数组的值[事件最早发生时间]

bool ALGraph::TopologicalSort(int result[], int& count) {

	int stack[MAX_VERTEX];   //把顶点对应的下标压入堆栈

	int top = -1;
	int inVex; 
	int outVex;//遍历一个顶点的所有邻接边结点时,用outVex暂存当前处理的顶点
	ArcNode* p;

	//初始化事件最早发生时间ve数组
	for (int i = 0; i < vertexNum; i++) {
		ve[i] = 0;
	}
	//遍历顶点表，把入度为0的压栈
	for (int i = 0; i < vertexNum; i++) {
		if (adjList[i].in == 0) {
			stack[++top] = i;
		}
	}
	//完成拓扑排序
	count = 0;

	//当堆栈不为空时
	while (top != -1) {
		inVex = stack[top--];
		result[count] = inVex;
		count++;

		//找到当前处理的顶点的所有出边
		p = adjList[inVex].firstEdge;
		while (p) {
			outVex = p->adjvex;
			adjList[outVex].in--;
			if (0 == adjList[outVex].in) {
				stack[++top] = outVex;
				//刚才入度为0的节点已经出栈了，
				//原来存放刚出栈节点的位置存放下一个入度为0的节点
				//top改变了，还得回到原来的位置。先++
			}

			if (ve[inVex] + p->weight > ve[outVex]) {
				ve[outVex] = ve[inVex] + p->weight;
			}   //计算事件最早发生时间

			p = p->next;
		}
	}
	//判断拓扑排序是否正确
	if (count == vertexNum) {
		return true;
	}
	else {
		return false;
	}
}

创建邻接表

需要在边表中增加权值weight

在顶点表中增加一个字段in

struct ArcNode { //边表
	int weight;     //增加权值分量，代表活动时间
	int adjvex;
	ArcNode* next;
};

struct VertexNode { //顶点表
	int in;                //增加入度字段
	char vertex;
	ArcNode* firstEdge;
};

给定一个起点，终点，权值，对图中数据进行设置

bool ALGraph::setEdge(int vi, int vj, int weight) { 
	//修改setEdge函数，把vj顶点表中的入度+1 
	ArcNode* s;
	if (vi >= 0 && vi < vertexNum && vj >= 0 && vj < vertexNum && vi != vj) {
		//创建一个边结点vj
		s = new ArcNode;
		s->adjvex = vj;
		s->weight = weight; 
		//把边结点vj插入到顶点表vi项的邻接表中，成为第一个结点
		s->next = adjList[vi].firstEdge;
		adjList[vi].firstEdge = s;
		//vj顶点表中的入度+1 
		adjList[vj].in++;
		return true;
	}
	else {
		return false;
	}
}

代码调试

输入

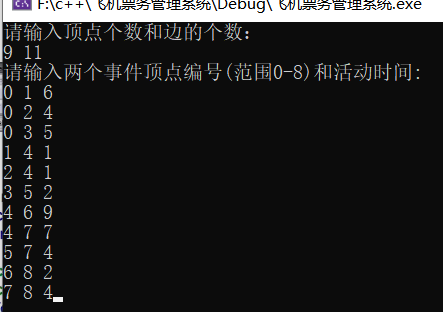
输出

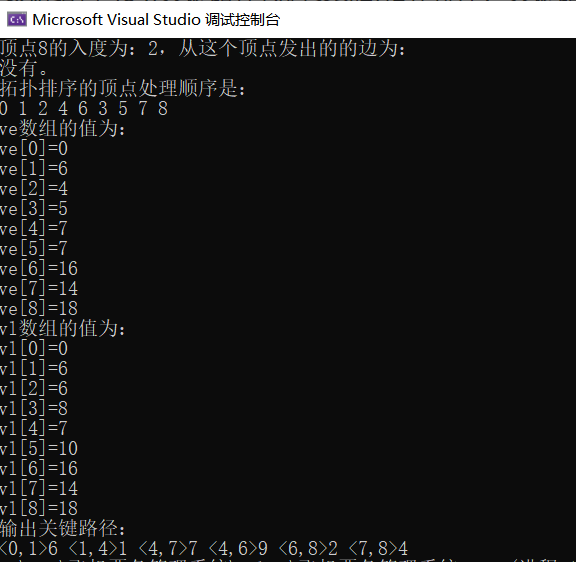
源代码

#include <iostream>
#include <stdio.h>
using namespace std;

const int MAX_VERTEX = 30;    //图的最大顶点数

struct ArcNode { //边表
	int weight;     //增加权值分量，代表活动时间
	int adjvex;
	ArcNode* next;
};

struct VertexNode { //顶点表
	int in;                //增加入度字段
	char vertex;
	ArcNode* firstEdge;
};

class ALGraph {
private:
	VertexNode* adjList;  //邻接表
	int vertexNum, arcNum;
	int* ve, * vl; //ve数组是事件最早发生时间，vl事件最迟发生时间
public:
	ALGraph(char v[], int n, int e);  
	~ALGraph();           
	void inputEdges();      
	bool setEdge(int vi, int vj, int weight);   
	void displayData();//显示函数信息

	bool TopologicalSort(int result[], int& count); 
	bool CriticalPath();  
};

ALGraph::ALGraph(char v[], int n, int e) {
	vertexNum = n;
	arcNum = e;
	adjList = new VertexNode[vertexNum];
	for (int i = 0; i < vertexNum; i++) {
		//输入顶点信息，初始化顶点表
		adjList[i].in = 0;    //增加in的初始化
		adjList[i].vertex = v[i];
		adjList[i].firstEdge = NULL;
	}
	ve = new int[vertexNum];
	vl = new int[vertexNum];

}
ALGraph ::~ALGraph() {
	ArcNode* p, * pre;
	//遍历顶点表数组，把顶点表指向的所有边结点删除
	for (int i = 0; i < vertexNum; i++) {
		p = adjList[i].firstEdge;
		adjList[i].firstEdge = NULL;
		while (p) {
			pre = p;
			p = p->next;
			delete pre;
		}
	}
	delete[] adjList;
	delete[] ve;
	delete[] vl;
}

void ALGraph::inputEdges() { 
	cout << "请输入两个事件顶点编号(范围0-" << vertexNum - 1 << ")和活动时间:" << endl;
	for (int i = 0; i < arcNum; i++) {
		//输入边的信息存储在边表中
		int vi, vj, weight;
		cin >> vi >> vj >> weight;   //输入边依附的两个顶点的编号
		if (!setEdge(vi, vj, weight)) {
			cout << "输入的顶点编号超过范围或者相等，需要重新输入" << endl;
			i--;
		}
	}
}

bool ALGraph::setEdge(int vi, int vj, int weight) { 
	//修改setEdge函数，把vj顶点表中的入度+1 
	ArcNode* s;
	if (vi >= 0 && vi < vertexNum && vj >= 0 && vj < vertexNum && vi != vj) {
		//创建一个边结点vj
		s = new ArcNode;
		s->adjvex = vj;
		s->weight = weight; 
		//把边结点vj插入到顶点表vi项的邻接表中，成为第一个结点
		s->next = adjList[vi].firstEdge;
		adjList[vi].firstEdge = s;
		//vj顶点表中的入度+1   
		adjList[vj].in++;
		return true;
	}
	else {
		return false;
	}
}


void ALGraph::displayData() {
	ArcNode* p;
	cout << "输出图的存储情况：" << endl;
	for (int i = 0; i < vertexNum; i++) {
		cout << "顶点" << adjList[i].vertex << "的入度为：" << adjList[i].in << "，从这个顶点发出的的边为：" << endl; //-----
		p = adjList[i].firstEdge;
		if (!p)
			cout << "没有。" << endl;
		while (p) {
			cout << "<" << i << "," << p->adjvex << ">" << p->weight << endl;
			p = p->next;
		}
	}
}

bool ALGraph::TopologicalSort(int result[], int& count) {

	//把result数组看作是栈
	int stack[MAX_VERTEX];   //把顶点对应的下标压入堆栈

	int top = -1;
	int inVex; //用来保存从堆栈中弹出的顶点（下标）
	int outVex;//遍历一个顶点的所有邻接边结点时,用outVex暂存当前处理的顶点
	ArcNode* p;

	//初始化事件最早发生时间ve数组
	for (int i = 0; i < vertexNum; i++) {
		ve[i] = 0;
	}
	//遍历顶点表，把入度为0的压栈
	for (int i = 0; i < vertexNum; i++) {
		if (adjList[i].in == 0) {
			stack[++top] = i;
		}
	}
	//完成拓扑排序
	count = 0;

	//当堆栈不为空时
	while (top != -1) {
		inVex = stack[top--];
		result[count] = inVex;
		count++;

		//找到当前处理的顶点的所有出边
		p = adjList[inVex].firstEdge;
		while (p) {
			outVex = p->adjvex;
			adjList[outVex].in--;
			if (0 == adjList[outVex].in) {
				stack[++top] = outVex;
				//刚才入度为0的节点已经出栈了，
				//原来存放刚出栈节点的位置存放下一个入度为0的节点
				//top改变了，还得回到原来的位置。先++
			}

			if (ve[inVex] + p->weight > ve[outVex]) {
				ve[outVex] = ve[inVex] + p->weight;
			}   //计算事件最早发生时间

			p = p->next;
		}
	}
	//判断拓扑排序是否正确
	if (count == vertexNum) {
		return true;
	}
	else {
		return false;
	}
}

bool ALGraph::CriticalPath() {

	int resultStack[MAX_VERTEX]; //存储拓扑排序结果序列(存储下标)
	int resultTop;               //拓扑排序有效顶点个数(栈顶指针)
	ArcNode* p;
	int count;
	int inVex, outVex;  //inVex,outVex，分别代表一条边的起点顶点号和终点顶点号

	if (!TopologicalSort(resultStack, count)) {
		return false;
	}

	//输出拓扑排序的顶点处理顺序
	cout << "拓扑排序的顶点处理顺序是：" << endl;
	for (int i = 0; i < count; i++) {
		cout << resultStack[i] << " ";
	}
	cout << endl;


	//输出ve数组的值
	cout << "ve数组的值为：" << endl;
	for (int i = 0; i < count; i++) {
		cout << "ve[" << i << "]=" << ve[i] << endl;
	}


	//求解vl数组的值
	resultTop = count - 1;
	inVex = resultStack[resultTop--];   //汇点出栈
	for (int i = 0; i < vertexNum; i++) {
		vl[i] = ve[inVex]; //用最大值初始化
	}

	//栈不为空时，按拓扑逆序求各个顶点的vl值
	while (resultTop != -1) {
		inVex = resultStack[resultTop--];
		p = adjList[inVex].firstEdge;
		while (p) {
			outVex = p->adjvex;
			if (vl[inVex] > vl[outVex] - p->weight) {
				vl[inVex] = vl[outVex] - p->weight;
			}
			p = p->next;
		}
	}
	cout << "vl数组的值为：" << endl;
	for (int i = 0; i < count; i++) {
		cout << "vl[" << i << "]=" << vl[i] << endl;
	}


	cout << "输出关键路径：" << endl;

	//从上往下扫描顶点表，处理每个顶点的边表
	for (inVex = 0; inVex < vertexNum; inVex++) {
		p = adjList[inVex].firstEdge;
		while (p) {
			outVex = p->adjvex;
			int weight = p->weight;
			int ee = ve[inVex];
			int el = vl[outVex] - weight;

			if (ee == el) {
				cout << "<" << inVex << "," << outVex << ">" << weight << " ";
			}
			p = p->next;
		}
	}
	return true;
}


int main() {
	char vertex[MAX_VERTEX];
	int num, edge;

	cout << "请输入顶点个数和边的个数：";
	cin >> num >> edge;
	for (int i = 0; i < num; i++)
		vertex[i] = i + '0';

	ALGraph graph(vertex, num, edge);
	graph.inputEdges();
	graph.displayData();

	if (!graph.CriticalPath()) {
		cout << "这个图有回路，不能求关键路径。";
	}

	return 0;
}