Tensorflow（2）：MNIST识别自己手写的数字--进阶篇（CNN）

   本文利用卷积神经网络（CNN）实现自己手写的数字识别。主要参考自Tensorflow中文社区官方教程【Minst进阶】

1.卷积神经网络简介

  卷积神经网络是一种多层神经网络，擅长处理图像特别是大图像的相关机器学习问题。
  卷积网络通过一系列方法，将数据量庞大的图像识别问题不断降维，最终使其能够被训练。CNN最早由Yann LeCun提出并应用在手写字体识别上（MINST），其提出的网络称为LeNet-5，结构如下：

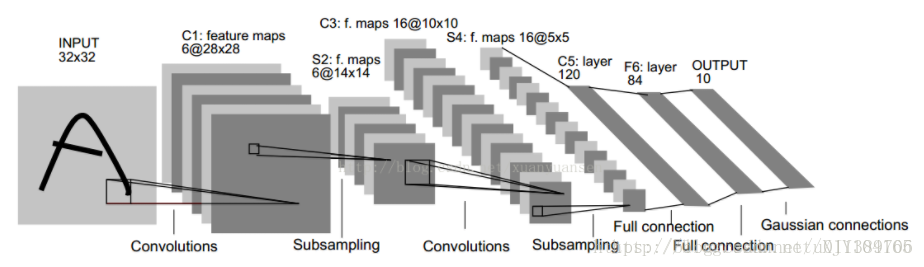
  该网络由卷积层、池化层、全连接层组成。其中卷积层与池化层配合，组成多个卷积组，逐层提取特征，最终通过若干个全连接层完成分类。

 1.1 卷积（Convolutions）

  自然图像有其固有特性，也就是说，图像的一部分的统计特性与其他部分是一样的，这也意味着我们在这一部分学习的特征也能用在另一部分上。

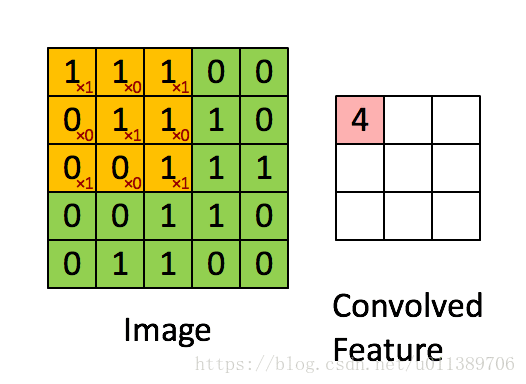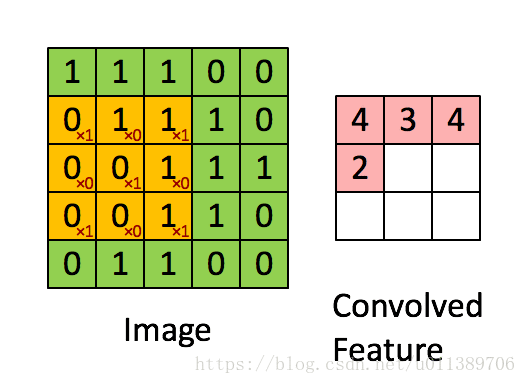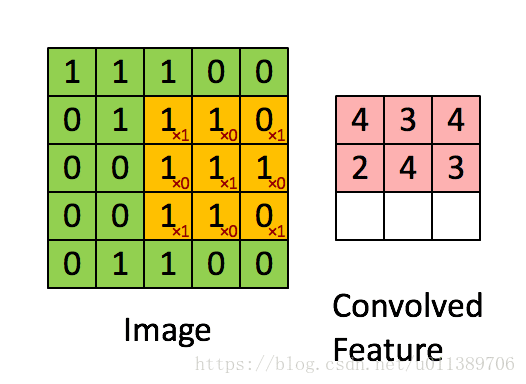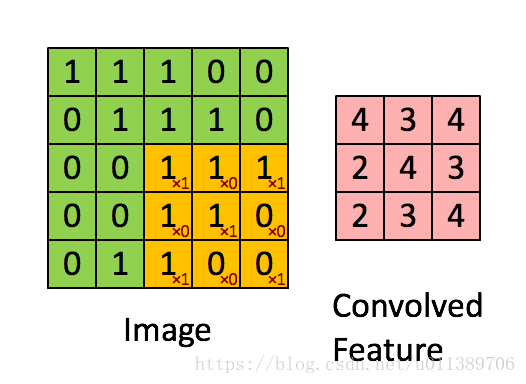
  总结下convolution的处理过程：
  假设给定了r * c的大尺寸图像，将其定义为xlarge。首先通过从大尺寸图像中抽取的a * b的小尺寸图像样本xsmall训练稀疏自编码，得到了k个特征（k为隐含层神经元数量），然后对于xlarge中的每个a*b大小的块，求激活值fs，然后对这些fs进行卷积。这样得到（r-a+1）*（c-b+1）*k个卷积后的特征矩阵。

 1.2 池化（又叫子采样Subsampling）

  在通过卷积获得了特征（features）之后，下一步我们希望利用这些特征去做分类。理论上讲，人们可以把所有解析出来的特征关联到一个分类器，例如softmax分类器，但计算量非常大。例如：对于一个96X96像素的图像，假设我们已经通过8X8个输入学习得到了400个特征。而每一个卷积都会得到一个(96 − 8 + 1) * (96 − 8 + 1) = 7921的结果集，由于已经得到了400个特征，所以对于每个样例（example）结果集的大小就将达到892 * 400 = 3,168,400 个特征。这样学习一个拥有超过3百万特征的输入的分类器是相当不明智的，并且极易出现过度拟合（over-fitting）.

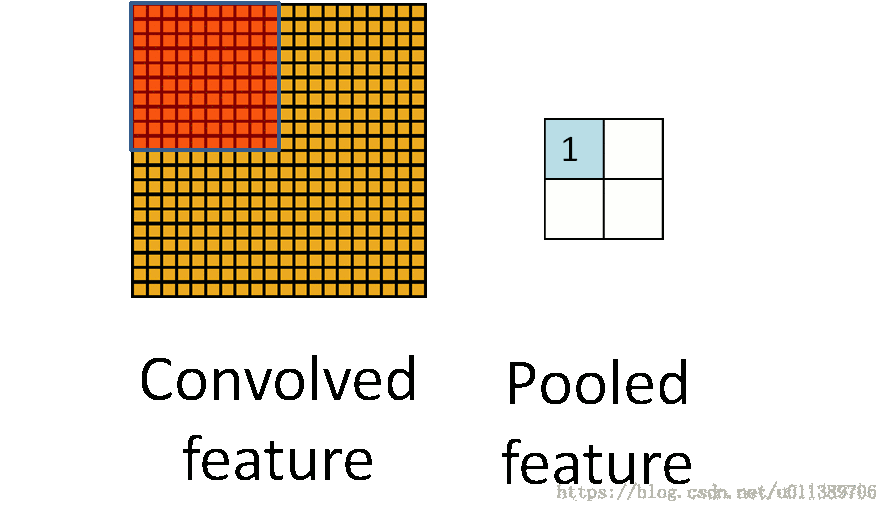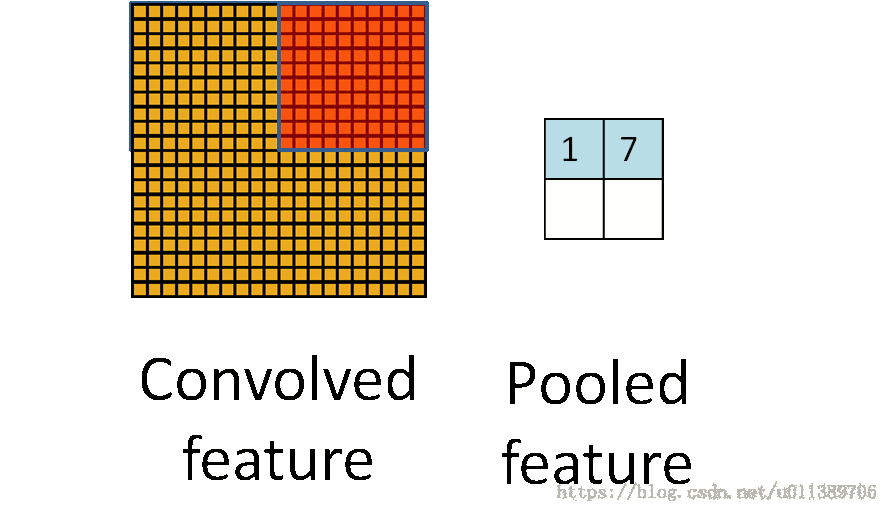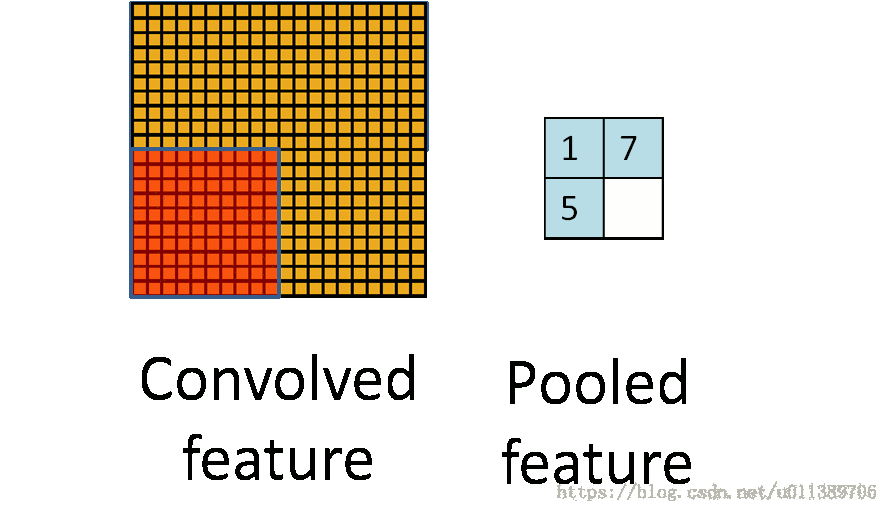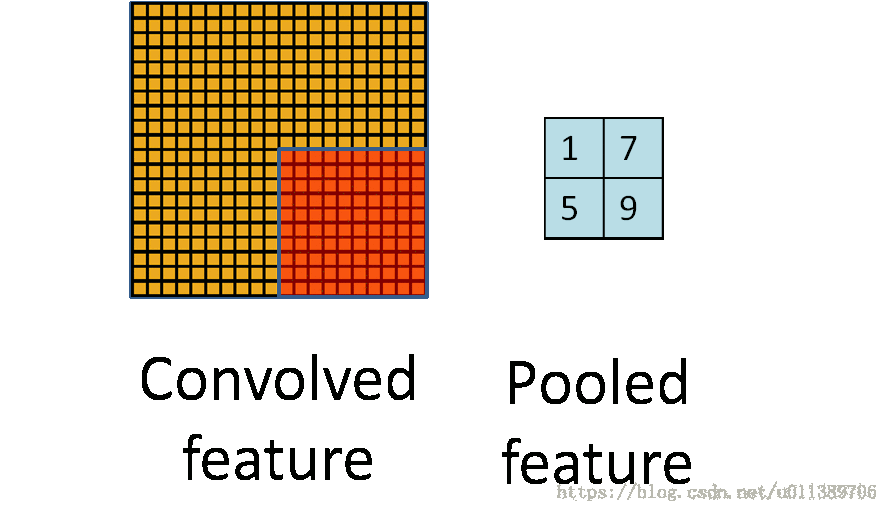
  所以就有了pooling这个方法，其实也就是把特征图像区域的一部分求个均值或者最大值，用来代表这部分区域。如果是求均值就是mean pooling，求最大值就是max pooling。

2.模型训练及保存

   根据前面的原理，我们搭建CNN网络对数据进行训练，训练数据来自【Yann LeCun’s MNIST page】。该训练代码改编自Tensorflow中文社区官方教程【Minst进阶】

#-*- coding: UTF-8 -*-
import tensorflow as tf
import input_data

mnist = input_data.read_data_sets('MNIST_data', one_hot=True)   # one_hot 编码 [1 0 0 0]
sess = tf.InteractiveSession()

x = tf.placeholder("float", shape=[