Growth of Functions - Introduction to Algorithm - Summary of Chapter 3

Asymptotic notation

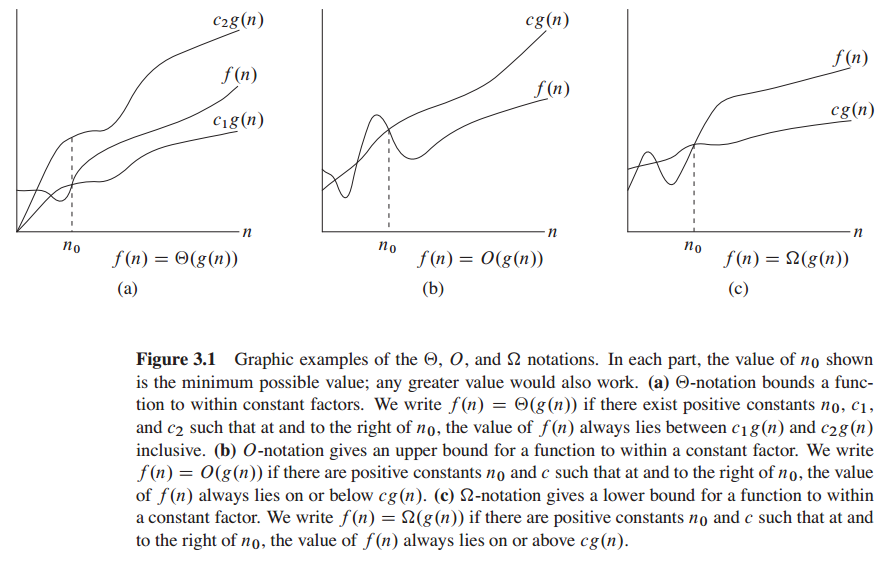
$\Theta$ -notation : asymptotically tight bound
$\Theta (g(n)) =\{ f(n):$ there exist positive constans $c_1, c_2,$ and $n_0$ such that$0\le c_1g(n)\le f(n) \le c_2g(n)$ for all $n \ge n_0\}$
Every member$f(n) = \Theta(g(n))$ be asymptotically nonnegative

$g(n)$ is an asymptotically tight bound for $f(n)$ : For any $n \ge n_0$, the function $f(n)$ is equal to $g(n)$ to within a constant factor.

$O$-notation : asymptotic upper bound
$O(g(n)) = \{ f(n)$: there exist positive constant $c$ and $n_0$ such that $0\le f(n) \le cg(n)$ for all $n\ge n_0 \}$

$\Omega$-notation : asymptotic lower bound
$\Omega(g(n)) = \{ f(n)$: there exist positive constant $c$ and $n_0$ such that $0\le cg(n) \le f(n)$ for all $n\ge n_0 \}$

The $\Theta$-notation is a stronger notation that $O$-notation and $\Omega$-notation.

Theorem 3.1
For any two functions $f(n)$ and $g(n)$ , we have $f(n) = \Theta (g(n))$ if and only if $f(n) = O(g(n))$ and $f(n) = \Theta(g(n))$

$o$-notation : asymptotic upper bound (not tight)
$O(g(n)) = \{ f(n)$: there exist positive constant $c$ and $n_0$ such that $0\le f(n)< cg(n)$ for all $n\ge n_0 \}$

$\omega$-notation : asymptotic lower bound
$\omega(g(n)) = \{ f(n)$: there exist positive constant $c$ and $n_0$ such that $0\le cg(n) < f(n)$ for all $n\ge n_0 \}$

---

Comparing function

Transitivity :
$f(n)=\Theta(g(n))$ and $g(n) = \Theta(h(n))$ imply $f(n) = \Theta(h(n))$
$f(n)=O(g(n))$ and $g(n) = O(h(n))$ imply $f(n) = O(h(n))$
$f(n)=\Omega(g(n))$ and $g(n) = \Omega(h(n))$ imply $f(n) = \Omega(h(n))$
$f(n)=o(g(n))$ and $g(n) = o(h(n))$ imply $f(n) = o(h(n))$
$f(n)=\omega(g(n))$ and $g(n) = \omega(h(n))$ imply $f(n) = \omega(h(n))$

Reflexivity:
$f(n) = \Theta(f(n))$
$f(n) = O(f(n))$
$f(n) = \Omega(f(n))$

Symmetry:
$f(n) = \Theta(g(n))$ if and only if $g(n) = \Theta(f(n))$

Transpose symmetry
$f(n) = O(g(n))$ if and only if $g(n) = \Omega(f(n))$
$f(n) = o(g(n))$ if and only if $g(n) = \omega(f(n))$

$f(n)=O(g(n))$ is like $a\le b$
$f(n)=\Omega(g(n))$ is like $a\ge b$
$f(n)=\Theta(g(n))$ is like $a= b$
$f(n)=o(g(n))$ is like $a< b$
$f(n)=\omega(g(n))$ is like $a> b$

Some of above content refere to “Introduction to Algorithm”.

---

Monotonicity
A function $f(n)$ is monotonically increasing if $m\le n$ implies $f(m) \le f(n)$. Similarly, it is monotonically decreasing if $m\le n$ implies $f(m) \ge f(n)$. A
function $f(n)$ is strictly increasing if $m < n$ implies $f(m) < f(n)$ and strictly
decreasing if $m < n$ implies $f(m) > f(n)$.

Floors and ceilings
the greatest integer less than or equal to x by $\lfloor x\rfloor$. the least integer greater than or equal to x by $\lceil x \rceil$.

Modular arithmetic
a mod n is the remainder of the quotient $a/n$.If .a mod n = b mod n, we write a$\equiv$b (mod n) and say that a is equivalent to b, modulo n.

Some of above content refere to “Introduction to Algorithm”.