零基础入门深度学习(3) - 神经网络和反向传播算法

最新推荐文章于 2022-07-20 16:09:16 发布

Godswisdom

最新推荐文章于 2022-07-20 16:09:16 发布

阅读量3.9k

点赞数 9

分类专栏：深度学习数学基础文章标签：深度学习入门系列神经网络反向传播算法

深度学习同时被 2 个专栏收录

24 篇文章 12 订阅

订阅专栏

数学基础

7 篇文章 2 订阅

订阅专栏

零基础入门深度学习(3) - 神经网络和反向传播算法

文献内容来自：https://www.zybuluo.com/hanbingtao/note/476663

在这里插入图片描述

无论即将到来的是大数据时代还是人工智能时代，亦或是传统行业使用人工智能在云上处理大数据的时代，作为一个有理想有追求的程序员，不懂深度学习（Deep Learning）这个超热的技术，会不会感觉马上就out了？现在救命稻草来了，《零基础入门深度学习》系列文章旨在讲帮助爱编程的你从零基础达到入门级水平。零基础意味着你不需要太多的数学知识，只要会写程序就行了，没错，这是专门为程序员写的文章。虽然文中会有很多公式你也许看不懂，但同时也会有更多的代码，程序员的你一定能看懂的（我周围是一群狂热的Clean Code程序员，所以我写的代码也不会很差）。

0 文章列表

零基础入门深度学习(1) - 感知器
 零基础入门深度学习(2) - 线性单元和梯度下降
 零基础入门深度学习(3) - 神经网络和反向传播算法
 零基础入门深度学习(4) - 卷积神经网络
 零基础入门深度学习(5) - 循环神经网络
 零基础入门深度学习(6) - 长短时记忆网络(LSTM)
零基础入门深度学习(7) - 递归神经网络

1 往期回顾

在上一篇文章中，我们已经掌握了机器学习的基本套路，对模型、目标函数、优化算法这些概念有了一定程度的理解，而且已经会训练单个的感知器或者线性单元了。在这篇文章中，我们将把这些单独的单元按照一定的规则相互连接在一起形成神经网络，从而奇迹般的获得了强大的学习能力。我们还将介绍这种网络的训练算法：反向传播算法。最后，我们依然用代码实现一个神经网络。如果您能坚持到本文的结尾，将会看到我们用自己实现的神经网络去识别手写数字。现在请做好准备，您即将双手触及到深度学习的大门。

2 神经元

神经元和感知器本质上是一样的，只不过我们说感知器的时候，它的激活函数是阶跃函数；而当我们说神经元时，激活函数往往选择为sigmoid函数或tanh函数。如下图所示：

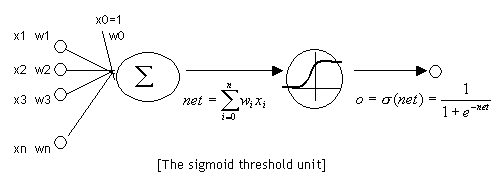
计算一个神经元的输出的方法和计算一个感知器的输出是一样的。假设神经元的输入是向量 $\vec{x}$ ，权重向量是 $\vec{w}$ (偏置项是 $w_0$ )，激活函数是sigmoid函数，则其输出： $y=sigmoid(\vec{w}^T\centerdot\vec{x})\qquad(式1)$

sigmoid函数的定义如下： $sigmoid(x)=\frac{1}{1+e^{-x}}$

将其带入前面的式子，得到 $y=\frac{1}{1+e^{-\vec{w}^T\centerdot\vec{x}}}$

sigmoid函数是一个非线性函数，值域是(0,1)。函数图像如下图所示

sigmoid函数的导数是： $\begin{aligned} &令y=sigmoid(x)\\ &则y'=y(1-y) \end{aligned}$

可以看到，sigmoid函数的导数非常有趣，它可以用sigmoid函数自身来表示。这样，一旦计算出sigmoid函数的值，计算它的导数的值就非常方便。

3 神经网络是啥

神经网络其实就是按照一定规则连接起来的多个神经元。上图展示了一个全连接(full connected, FC)神经网络，通过观察上面的图，我们可以发现它的规则包括：

神经元按照层来布局。最左边的层叫做输入层，负责接收输入数据；最右边的层叫输出层，我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层，因为它们对于外部来说是不可见的。
同一层的神经元之间没有连接。
第N层的每个神经元和第N-1层的所有神经元相连(这就是full connected的含义)，第N-1层神经元的输出就是第N层神经元的输入。
每个连接都有一个权值。

上面这些规则定义了全连接神经网络的结构。事实上还存在很多其它结构的神经网络，比如卷积神经网络(CNN)、循环神经网络(RNN)，他们都具有不同的连接规则。

4 计算神经网络的输出

神经网络实际上就是一个输入向量 $\vec{x}$ 到输出向量 $\vec{y}$ 的函数，即：
$\vec{y} = f_{network}(\vec{x})$

根据输入计算神经网络的输出，需要首先将输入向量 $\vec{x}$ 的每个元素 $x_i$ 的值赋给神经网络的输入层的对应神经元，然后根据式1依次向前计算每一层的每个神经元的值，直到最后一层输出层的所有神经元的值计算完毕。最后，将输出层每个神经元的值串在一起就得到了输出向量 $\vec{y}$ 。

接下来举一个例子来说明这个过程，我们先给神经网络的每个单元写上编号。

如上图，输入层有三个节点，我们将其依次编号为1、2、3；隐藏层的4个节点，编号依次为4、5、6、7；最后输出层的两个节点编号为8、9。因为我们这个神经网络是全连接网络，所以可以看到每个节点都和上一层的所有节点有连接。比如，我们可以看到隐藏层的节点4，它和输入层的三个节点1、2、3之间都有连接，其连接上的权重分别为 $w_{41},w_{42},w_{43}$ 。那么，我们怎样计算节点4的输出值 $a_4$ 呢？

为了计算节点4的输出值，我们必须先得到其所有上游节点（也就是节点1、2、3）的输出值。节点1、2、3是输入层的节点，所以，他们的输出值就是输入向量 $\vec{x}$ 本身。按照上图画出的对应关系，可以看到节点1、2、3的输出值分别是 $x_1,x_2,x_3$ 。我们要求输入向量的维度和输入层神经元个数相同，而输入向量的某个元素对应到哪个输入节点是可以自由决定的，你偏非要把赋值给节点2也是完全没有问题的，但这样除了把自己弄晕之外，并没有什么价值。

一旦我们有了节点1、2、3的输出值，我们就可以根据式1计算节点4的输出值 $a_4$ ：
$\begin{aligned} a_4&=sigmoid(\vec{w}^T\centerdot\vec{x})\\ &=sigmoid(w_{41}x_1+w_{42}x_2+w_{43}x_3+w_{4b}) \end{aligned}$

上式的 $w_{4b}$ 是节点4的偏置项，图中没有画出来。而 $w_{41},w_{42},w_{43}$ 分别为节点1、2、3到节点4连接的权重 $w_{ji}$ ，在给权重编号时，我们把目标节点的编号放在前面，把源节点的编号放在后面。

同样，我们可以继续计算出节点5、6、7的输出值 $a_5,a_6,a_7$ 。这样，隐藏层的4个节点的输出值就计算完成了，我们就可以接着计算输出层的节点8的输出值 $y_1$ ：
$\begin{aligned} y_1&=sigmoid(\vec{w}^T\centerdot\vec{a})\\ &=sigmoid(w_{84}a_4+w_{85}a_5+w_{86}a_6+w_{87}a_7+w_{8b}) \end{aligned}$

同理，我们还可以计算出 $y_2$ 的值。这样输出层所有节点的输出值计算完毕，我们就得到了在输入向量 $\vec{x}=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$ 时，神经网络的输出向量 $\vec{y}=\begin{bmatrix}y_1\\y_2\end{bmatrix}$ 。这里我们也看到，输出向量的维度和输出层神经元个数相同。

4.1 神经网络的矩阵表示

神经网络的计算如果用矩阵来表示会很方便（当然逼格也更高），我们先来看看隐藏层的矩阵表示。

首先我们把隐藏层4个节点的计算依次排列出来：
$a_4=sigmoid(w_{41}x_1+w_{42}x_2+w_{43}x_3+w_{4b})\\ a_5=sigmoid(w_{51}x_1+w_{52}x_2+w_{53}x_3+w_{5b})\\ a_6=sigmoid(w_{61}x_1+w_{62}x_2+w_{63}x_3+w_{6b})\\ a_7=sigmoid(w_{71}x_1+w_{72}x_2+w_{73}x_3+w_{7b})$

接着，定义网络的输入向量 $\vec{x}$ 和隐藏层每个节点的权重向量 $\vec{w_j}$ 。令
$\begin{aligned} \vec{x}&=\begin{bmatrix}x_1\\x_2\\x_3\\1\end{bmatrix}\\ \vec{w}_4&=[w_{41},w_{42},w_{43},w_{4b}]\\ \vec{w}_5&=[w_{51},w_{52},w_{53},w_{5b}]\\ \vec{w}_6&=[w_{61},w_{62},w_{63},w_{6b}]\\ \vec{w}_7&=[w_{71},w_{72},w_{73},w_{7b}]\\ f&=sigmoid \end{aligned}$

代入到前面的一组式子，得到：
$\begin{aligned} a_4&=f(\vec{w_4}\centerdot\vec{x})\\ a_5&=f(\vec{w_5}\centerdot\vec{x})\\ a_6&=f(\vec{w_6}\centerdot\vec{x})\\ a_7&=f(\vec{w_7}\centerdot\vec{x}) \end{aligned}$

现在，我们把上述计算 $a_4,a_5,a_6,a_7$ 的四个式子写到一个矩阵里面，每个式子作为矩阵的一行，就可以利用矩阵来表示它们的计算了。令
$\vec{a}= \begin{bmatrix} a_4 \\ a_5 \\ a_6 \\ a_7 \\ \end{bmatrix},\qquad W= \begin{bmatrix} \vec{w}_4 \\ \vec{w}_5 \\ \vec{w}_6 \\ \vec{w}_7 \\ \end{bmatrix}= \begin{bmatrix} w_{41},w_{42},w_{43},w_{4b} \\ w_{51},w_{52},w_{53},w_{5b} \\ w_{61},w_{62},w_{63},w_{6b} \\ w_{71},w_{72},w_{73},w_{7b} \\ \end{bmatrix} ,\qquad f( \begin{bmatrix} x_1\\ x_2\\ x_3\\ .\\ .\\ .\\ \end{bmatrix})= \begin{bmatrix} f(x_1)\\ f(x_2)\\ f(x_3)\\ .\\ .\\ .\\ \end{bmatrix}$

带入前面的一组式子，得到
$\vec{a}=f(W\centerdot\vec{x})\qquad (式2)$

在式2中， $f$ 是激活函数，在本例中是sigmoid函数； $W$ 是某一层的权重矩阵； $\vec {x}$ 是某层的输入向量； $\vec {a}$ 是某层的输出向量。式2说明神经网络的每一层的作用实际上就是先将输入向量左乘一个数组进行线性变换，得到一个新的向量，然后再对这个向量逐元素应用一个激活函数。

每一层的算法都是一样的。比如，对于包含一个输入层，一个输出层和三个隐藏层的神经网络，我们假设其权重矩阵分别为 $W_1,W_2,W_3,W_4$ ，每个隐藏层的输出分别是 $\vec{a}_1,\vec{a}_2,\vec{a}_3$ ，神经网络的输入为 $\vec {x}$ ，神经网络的输入为 $\vec {y}$ ，如下图所示：

则每一层的输出向量的计算可以表示为：
$\begin{aligned} &\vec{a}_1=f(W_1\centerdot\vec{x})\\ &\vec{a}_2=f(W_2\centerdot\vec{a}_1)\\ &\vec{a}_3=f(W_3\centerdot\vec{a}_2)\\ &\vec{y}=f(W_4\centerdot\vec{a}_3)\\ \end{aligned}$

这就是神经网络输出值的计算方法。

5 神经网络的训练

现在，我们需要知道一个神经网络的每个连接上的权值是如何得到的。我们可以说神经网络是一个模型，那么这些权值就是模型的参数，也就是模型要学习的东西。然而，一个神经网络的连接方式、网络的层数、每层的节点数这些参数，则不是学习出来的，而是人为事先设置的。对于这些人为设置的参数，我们称之为超参数(Hyper-Parameters)。

接下来，我们将要介绍神经网络的训练算法：反向传播算法。

5.1 反向传播算法(Back Propagation)

我们首先直观的介绍反向传播算法，最后再来介绍这个算法的推导。当然读者也可以完全跳过推导部分，因为即使不知道如何推导，也不影响你写出来一个神经网络的训练代码。事实上，现在神经网络成熟的开源实现多如牛毛，除了练手之外，你可能都没有机会需要去写一个神经网络。

我们以监督学习为例来解释反向传播算法。在零基础入门深度学习(2) - 线性单元和梯度下降一文中我们介绍了什么是监督学习，如果忘记了可以再看一下。另外，我们设神经元的激活函数为函数(不同激活函数的计算公式不同，详情见反向传播算法的推导一节)。

我们假设每个训练样本为 $(\vec{x},\vec{t})$ ，其中向量 $\vec {x}$ 是训练样本的特征，而 $\vec {t}$ 是样本的目标值。

首先，我们根据上一节介绍的算法，用样本的特征 $\vec {x}$ ，计算出神经网络中每个隐藏层节点的输出 $\vec {a_i}$ ，以及输出层每个节点的输出 $\vec {y_i}$ 。

然后，我们按照下面的方法计算出每个节点的误差项 $\delta_i$ ：

对于输出层节点 $i$ ，
$\delta_i=y_i(1-y_i)(t_i-y_i)\qquad(式3)$

其中， $\delta_i$ 是节点 $i$ 的误差项， $\vec {y_i}$ 是节点 $i$ 的输出值， $\vec {t_i}$ 是样本对应于节点 $i$ 的目标值。举个例子，根据上图，对于输出层节点8来说，它的输出值是 $y_1$ ，而样本的目标值是 $t_1$ ，带入上面的公式得到节点8的误差项 $\delta_8$ 应该是：
$\delta_8=y_1(1-y_1)(t_1-y_1)$

对于隐藏层节点，
$\delta_i=a_i(1-a_i)\sum_{k\in{outputs}}w_{ki}\delta_k\qquad(式4)$

其中， $\vec {a_i}$ 是节点的输出值， $w_{ki}$ 是节点 $i$ 到它的下一层节点 $k$ 的连接的权重， $\delta_k$ 是节点的下一层节点 $k$ 的误差项。例如，对于隐藏层节点4来说，计算方法如下：
$\delta_4=a_4(1-a_4)(w_{84}\delta_8+w_{94}\delta_9)$

最后，更新每个连接上的权值：
$w_{ji}\gets w_{ji}+\eta\delta_jx_{ji}\qquad(式5)$

其中， $w_{ji}$ 是节点 $i$ 到节点 $j$ 的权重， $\eta$ 是一个成为学习速率的常数， $\delta_j$ 是节点 $j$ 的误差项， $x_{ji}$ 是节点 $i$ 传递给节点 $j$ 的输入。例如，权重的更新方法如下：
$w_{84}\gets w_{84}+\eta\delta_8 a_4$

类似的，权重 $w_{41}$ 的更新方法如下：
$w_{41}\gets w_{41}+\eta\delta_4 x_1$

偏置项的输入值永远为1。例如，节点4的偏置项 $\delta_{4b}$ 应该按照下面的方法计算：
$w_{4b}\gets w_{4b}+\eta\delta_4$

我们已经介绍了神经网络每个节点误差项的计算和权重更新方法。显然，计算一个节点的误差项，需要先计算每个与其相连的下一层节点的误差项。这就要求误差项的计算顺序必须是从输出层开始，然后反向依次计算每个隐藏层的误差项，直到与输入层相连的那个隐藏层。这就是反向传播算法的名字的含义。当所有节点的误差项计算完毕后，我们就可以根据式5来更新所有的权重。

以上就是基本的反向传播算法，并不是很复杂，您弄清楚了么？

5.2 反向传播算法的推导

反向传播算法其实就是链式求导法则的应用。然而，这个如此简单且显而易见的方法，却是在Roseblatt提出感知器算法将近30年之后才被发明和普及的。对此，Bengio这样回应道：

很多看似显而易见的想法只有在事后才变得显而易见。

接下来，我们用链式求导法则来推导反向传播算法，也就是上一小节的式3、式4、式5。

前方高能预警——接下来是数学公式重灾区，读者可以酌情阅读，不必强求。

按照机器学习的通用套路，我们先确定神经网络的目标函数，然后用随机梯度下降优化算法去求目标函数最小值时的参数值。

我们取网络所有输出层节点的误差平方和作为目标函数：
$E_d\equiv\frac{1}{2}\sum_{i\in outputs}(t_i-y_i)^2$

其中， $E_d$ 表示是样本 $d$ 的误差。

然后，我们用文章零基础入门深度学习(2) - 线性单元和梯度下降中介绍的随机梯度下降算法对目标函数进行优化：
$w_{ji}\gets w_{ji}-\eta\frac{\partial{E_d}}{\partial{w_{ji}}}$

随机梯度下降算法也就是需要求出误差 $E_d$ 对于每个权重 $w_{ji}$ 的偏导数（也就是梯度），怎么求呢？

观察上图，我们发现权重w_{ji}仅能通过影响节点 $j$ 的输入值影响网络的其它部分，设 $net_j$ 是节点 $j$ 的加权输入，即
$\begin{aligned} net_j&=\vec{w_j}\centerdot\vec{x_j}\\ &=\sum_{i}{w_{ji}}x_{ji} \end{aligned}$

$E_d$ 是 $net_j$ 的函数， $net_j$ 而是w_{ji}的函数。根据链式求导法则，可以得到：
$\begin{aligned} \frac{\partial{E_d}}{\partial{w_{ji}}}&=\frac{\partial{E_d}}{\partial{net_j}}\frac{\partial{net_j}}{\partial{w_{ji}}}\\ &=\frac{\partial{E_d}}{\partial{net_j}}\frac{\partial{\sum_{i}{w_{ji}}x_{ji}}}{\partial{w_{ji}}}\\ &=\frac{\partial{E_d}}{\partial{net_j}}x_{ji} \end{aligned}$

上式中， $x_{ji}$ 是节点 $i$ 传递给节点 $j$ 的输入值，也就是节点 $i$ 的输出值。
对于 $\frac{\partial{E_d}}{\partial{net_j}}$ 的推导，需要区分输出层和隐藏层两种情况。

5.2.1 输出层权值训练

对于输出层来说， $net_j$ 仅能通过节点 $j$ 的输出值 $y_j$ 来影响网络其它部分，也就是说 $E_d$ 是 $y_j$ 的函数，而 $y_j$ 是 $net_j$ 的函数，其中 $y_j=sigmoid(net_j)$ 。所以我们可以再次使用链式求导法则：
$\begin{aligned} \frac{\partial{E_d}}{\partial{net_j}}&=\frac{\partial{E_d}}{\partial{y_j}}\frac{\partial{y_j}}{\partial{net_j}}\\ \end{aligned}$

考虑上式第一项:
$\begin{aligned} \frac{\partial{E_d}}{\partial{y_j}}&=\frac{\partial}{\partial{y_j}}\frac{1}{2}\sum_{i\in outputs}(t_i-y_i)^2\\ &=\frac{\partial}{\partial{y_j}}\frac{1}{2}(t_j-y_j)^2\\ &=-(t_j-y_j) \end{aligned}$

考虑上式第二项：
$\begin{aligned} \frac{\partial{y_j}}{\partial{net_j}}&=\frac{\partial sigmoid(net_j)}{\partial{net_j}}\\ &=y_j(1-y_j)\\ \end{aligned}$

将第一项和第二项带入，得到：
$\frac{\partial{E_d}}{\partial{net_j}}=-(t_j-y_j)y_j(1-y_j)$

如果令 $\delta_j=-\frac{\partial{E_d}}{\partial{net_j}}$ ，也就是一个节点的误差项 $\delta$ 是网络误差对这个节点输入的偏导数的相反数。带入上式，得到：
$\delta_j=(t_j-y_j)y_j(1-y_j)$

上式就是式3。

将上述推导带入随机梯度下降公式，得到：
$\begin{aligned} w_{ji}&\gets w_{ji}-\eta\frac{\partial{E_d}}{\partial{w_{ji}}}\\ &=w_{ji}+\eta(t_j-y_j)y_j(1-y_j)x_{ji}\\ &=w_{ji}+\eta\delta_jx_{ji} \end{aligned}$

上式就是式5。

5.2.2 隐藏层权值训练

现在我们要推导出隐藏层的 $\frac{\partial{E_d}}{\partial{net_j}}$ 。

首先，我们需要定义节点 $j$ 的所有直接下游节点的集合 $D o w n s t r e a m (j)$ 。例如，对于节点4来说，它的直接下游节点是节点8、节点9。可以看到 $net_j$ 只能通过影响 $D o w n s t r e a m (j)$ 再影响。设 $net_k$ 是节点 $j$ 的下游节点的输入，则 $E_d$ 是 $net_k$ 的函数，而 $net_k$ 是 $net_j$ 的函数。因为 $net_k$ 有多个，我们应用全导数公式，可以做出如下推导：
$\begin{aligned} \frac{\partial{E_d}}{\partial{net_j}}&=\sum_{k\in Downstream(j)}\frac{\partial{E_d}}{\partial{net_k}}\frac{\partial{net_k}}{\partial{net_j}}\\ &=\sum_{k\in Downstream(j)}-\delta_k\frac{\partial{net_k}}{\partial{net_j}}\\ &=\sum_{k\in Downstream(j)}-\delta_k\frac{\partial{net_k}}{\partial{a_j}}\frac{\partial{a_j}}{\partial{net_j}}\\ &=\sum_{k\in Downstream(j)}-\delta_kw_{kj}\frac{\partial{a_j}}{\partial{net_j}}\\ &=\sum_{k\in Downstream(j)}-\delta_kw_{kj}a_j(1-a_j)\\ &=-a_j(1-a_j)\sum_{k\in Downstream(j)}\delta_kw_{kj} \end{aligned}$

因为 $\delta_j=-\frac{\partial{E_d}}{\partial{net_j}}$ ，带入上式得到：
$\delta_j=a_j(1-a_j)\sum_{k\in Downstream(j)}\delta_kw_{kj}$

上式就是式4。

——数学公式警报解除——

至此，我们已经推导出了反向传播算法。需要注意的是，我们刚刚推导出的训练规则是根据激活函数是sigmoid函数、平方和误差、全连接网络、随机梯度下降优化算法。如果激活函数不同、误差计算方式不同、网络连接结构不同、优化算法不同，则具体的训练规则也会不一样。但是无论怎样，训练规则的推导方式都是一样的，应用链式求导法则进行推导即可。

6 神经网络的实现

完整代码请参考GitHub: https://github.com/hanbt/learn_dl/blob/master/bp.py (python2.7)

现在，我们要根据前面的算法，实现一个基本的全连接神经网络，这并不需要太多代码。我们在这里依然采用面向对象设计。

6.1 基本模型实现

首先，我们先做一个基本的模型：

如上图，可以分解出5个领域对象来实现神经网络：

Network 神经网络对象，提供API接口。它由若干层对象组成以及连接对象组成。
Layer 层对象，由多个节点组成。
Node 节点对象计算和记录节点自身的信息(比如输出值、误差项等)，以及与这个节点相关的上下游的连接。
Connection 每个连接对象都要记录该连接的权重。
Connections 仅仅作为Connection的集合对象，提供一些集合操作。

Node实现如下：

 # 节点类，负责记录和维护节点自身信息以及与这个节点相关的上下游连接，实现输出值和误差项的计算。
class Node(object):
    def __init__(self, layer_index, node_index):
        '''
        构造节点对象。
        layer_index: 节点所属的层的编号
        node_index: 节点的编号
        '''
        self.layer_index = layer_index
        self.node_index = node_index
        self.downstream = []
        self.upstream = []
        self.output = 0
        self.delta = 0
    def set_output(self, output):
        '''
        设置节点的输出值。如果节点属于输入层会用到这个函数。
        '''
        self.output = output
    def append_downstream_connection(self, conn):
        '''
        添加一个到下游节点的连接
        '''
        self.downstream.append(conn)
    def append_upstream_connection(self, conn):
        '''
        添加一个到上游节点的连接
        '''
        self.upstream.append(conn)
    def calc_output(self):
        '''
        根据式1计算节点的输出
        '''
        output = reduce(lambda ret, conn: ret + conn.upstream_node.output * conn.weight, self.upstream, 0)
        self.output = sigmoid(output)
    def calc_hidden_layer_delta(self):
        '''
        节点属于隐藏层时，根据式4计算delta
        '''
        downstream_delta = reduce(
            lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
            self.downstream, 0.0)
        self.delta = self.output * (1 - self.output) * downstream_delta
    def calc_output_layer_delta(self, label):
        '''
        节点属于输出层时，根据式3计算delta
        '''
        self.delta = self.output * (1 - self.output) * (label - self.output)
    def __str__(self):
        '''
        打印节点的信息
        '''
        node_str = '%u-%u: output: %f delta: %f' % (self.layer_index, self.node_index, self.output, self.delta)
        downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
        upstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.upstream, '')
        return node_str + '\n\tdownstream:' + downstream_str + '\n\tupstream:' + upstream_str

ConstNode对象，为了实现一个输出恒为1的节点(计算偏置项时需要)

class ConstNode(object):
    def __init__(self, layer_index, node_index):
        '''
        构造节点对象。
        layer_index: 节点所属的层的编号
        node_index: 节点的编号
        '''    
        self.layer_index = layer_index
        self.node_index = node_index
        self.downstream = []
        self.output = 1
    def append_downstream_connection(self, conn):
        '''
        添加一个到下游节点的连接
        '''       
        self.downstream.append(conn)
    def calc_hidden_layer_delta(self):
        '''
        节点属于隐藏层时，根据式4计算delta
        '''
        downstream_delta = reduce(
            lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
            self.downstream, 0.0)
        self.delta = self.output * (1 - self.output) * downstream_delta
    def __str__(self):
        '''
        打印节点的信息
        '''
        node_str = '%u-%u: output: 1' % (self.layer_index, self.node_index)
        downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
        return node_str + '\n\tdownstream:' + downstream_str

Layer对象，负责初始化一层。此外，作为Node的集合对象，提供对Node集合的操作。

class Layer(object):
    def __init__(self, layer_index, node_count):
        '''
        初始化一层
        layer_index: 层编号
        node_count: 层所包含的节点个数
        '''
        self.layer_index = layer_index
        self.nodes = []
        for i in range(node_count):
            self.nodes.append(Node(layer_index, i))
        self.nodes.append(ConstNode(layer_index, node_count))
    def set_output(self, data):
        '''
        设置层的输出。当层是输入层时会用到。
        '''
        for i in range(len(data)):
            self.nodes[i].set_output(data[i])
    def calc_output(self):
        '''
        计算层的输出向量
        '''
        for node in self.nodes[:-1]:
            node.calc_output()
    def dump(self):
        '''
        打印层的信息
        '''
        for node in self.nodes:
            print node

Connection对象，主要职责是记录连接的权重，以及这个连接所关联的上下游节点。

class Connection(object):
    def __init__(self, upstream_node, downstream_node):
        '''
        初始化连接，权重初始化为是一个很小的随机数
        upstream_node: 连接的上游节点
        downstream_node: 连接的下游节点
        '''
        self.upstream_node = upstream_node
        self.downstream_node = downstream_node
        self.weight = random.uniform(-0.1, 0.1)
        self.gradient = 0.0
    def calc_gradient(self):
        '''
        计算梯度
        '''
        self.gradient = self.downstream_node.delta * self.upstream_node.output
    def get_gradient(self):
        '''
        获取当前的梯度
        '''
        return self.gradient
    def update_weight(self, rate):
        '''
        根据梯度下降算法更新权重
        '''
        self.calc_gradient()
        self.weight += rate * self.gradient
    def __str__(self):
        '''
        打印连接信息
        '''
        return '(%u-%u) -> (%u-%u) = %f' % (
            self.upstream_node.layer_index, 
            self.upstream_node.node_index,
            self.downstream_node.layer_index, 
            self.downstream_node.node_index, 
            self.weight)

Connections对象，提供Connection集合操作。

class Connections(object):
    def __init__(self):
        self.connections = []
    def add_connection(self, connection):
        self.connections.append(connection)
    def dump(self):
        for conn in self.connections:
            print conn

Network对象，提供API。

class Network(object):
    def __init__(self, layers):
        '''
        初始化一个全连接神经网络
        layers: 二维数组，描述神经网络每层节点数
        '''
        self.connections = Connections()
        self.layers = []
        layer_count = len(layers)
        node_count = 0;
        for i in range(layer_count):
            self.layers.append(Layer(i, layers[i]))
        for layer in range(layer_count - 1):
            connections = [Connection(upstream_node, downstream_node) 
                           for upstream_node in self.layers[layer].nodes
                           for downstream_node in self.layers[layer + 1].nodes[:-1]]
            for conn in connections:
                self.connections.add_connection(conn)
                conn.downstream_node.append_upstream_connection(conn)
                conn.upstream_node.append_downstream_connection(conn)
    def train(self, labels, data_set, rate, iteration):
        '''
        训练神经网络
        labels: 数组，训练样本标签。每个元素是一个样本的标签。
        data_set: 二维数组，训练样本特征。每个元素是一个样本的特征。
        '''
        for i in range(iteration):
            for d in range(len(data_set)):
                self.train_one_sample(labels[d], data_set[d], rate)
    def train_one_sample(self, label, sample, rate):
        '''
        内部函数，用一个样本训练网络
        '''
        self.predict(sample)
        self.calc_delta(label)
        self.update_weight(rate)
    def calc_delta(self, label):
        '''
        内部函数，计算每个节点的delta
        '''
        output_nodes = self.layers[-1].nodes
        for i in range(len(label)):
            output_nodes[i].calc_output_layer_delta(label[i])
        for layer in self.layers[-2::-1]:
            for node in layer.nodes:
                node.calc_hidden_layer_delta()
    def update_weight(self, rate):
        '''
        内部函数，更新每个连接权重
        '''
        for layer in self.layers[:-1]:
            for node in layer.nodes:
                for conn in node.downstream:
                    conn.update_weight(rate)
    def calc_gradient(self):
        '''
        内部函数，计算每个连接的梯度
        '''
        for layer in self.layers[:-1]:
            for node in layer.nodes:
                for conn in node.downstream:
                    conn.calc_gradient()
    def get_gradient(self, label, sample):
        '''
        获得网络在一个样本下，每个连接上的梯度
        label: 样本标签
        sample: 样本输入
        '''
        self.predict(sample)
        self.calc_delta(label)
        self.calc_gradient()
    def predict(self, sample):
        '''
        根据输入的样本预测输出值
        sample: 数组，样本的特征，也就是网络的输入向量
        '''
        self.layers[0].set_output(sample)
        for i in range(1, len(self.layers)):
            self.layers[i].calc_output()
        return map(lambda node: node.output, self.layers[-1].nodes[:-1])
    def dump(self):
        '''
        打印网络信息
        '''
        for layer in self.layers:
            layer.dump()

至此，实现了一个基本的全连接神经网络。可以看到，同神经网络的强大学习能力相比，其实现还算是很容易的。

6.2 梯度检查

怎么保证自己写的神经网络没有BUG呢？事实上这是一个非常重要的问题。一方面，千辛万苦想到一个算法，结果效果不理想，那么是算法本身错了还是代码实现错了呢？定位这种问题肯定要花费大量的时间和精力。另一方面，由于神经网络的复杂性，我们几乎无法事先知道神经网络的输入和输出，因此类似TDD(测试驱动开发)这样的开发方法似乎也不可行。

办法还是有滴，就是利用梯度检查来确认程序是否正确。梯度检查的思路如下：

对于梯度下降算法：
$w_{ji}\gets w_{ji}-\eta\frac{\partial{E_d}}{\partial{w_{ji}}}$

来说，这里关键之处在于 $\frac{\partial{E_d}}{\partial{w_{ji}}}$ 的计算一定要正确，而它是对的偏导数。而根据导数的定义：
$f'(\theta)=\lim_{\epsilon->0}\frac{f(\theta+\epsilon)-f(\theta-\epsilon)}{2\epsilon}$

对于任意 $\theta$ 的导数值，我们都可以用等式右边来近似计算。我们把 $E_d$ 看做是 $w_{ji}$ 的函数，即 $E_d(w_{ji})$ ，那么根据导数定义， $\frac{\partial{E_d(w_{ji})}}{\partial{w_{ji}}}$ 应该等于：
$\frac{\partial{E_d(w_{ji})}}{\partial{w_{ji}}}=\lim_{\epsilon->0}\frac{f(w_{ji}+\epsilon)-f(w_{ji}-\epsilon)}{2\epsilon}$

如果把设置为一个很小的数（比如 $10^{-4}$ ），那么上式可以写成：
$\frac{\partial{E_d(w_{ji})}}{\partial{w_{ji}}}\approx\frac{f(w_{ji}+\epsilon)-f(w_{ji}-\epsilon)}{2\epsilon}\qquad(式6)$

我们就可以利用式6，来计算梯度 $\frac{\partial{E_d}}{\partial{w_{ji}}}$ 的值，然后同我们神经网络代码中计算出来的梯度值进行比较。如果两者的差别非常的小，那么就说明我们的代码是正确的。

下面是梯度检查的代码。如果我们想检查参数 $w_{ji}$ 的梯度是否正确，我们需要以下几个步骤：

首先使用一个样本 $d$ 对神经网络进行训练，这样就能获得每个权重的梯度
将 $w_{ji}$ 加上一个很小的值( $10^{-4}$ )，重新计算神经网络在这个样本 $d$ 下的 $E_{d+}$
将 $w_{ji}$ 减上一个很小的值( $10^{-4}$ )，重新计算神经网络在这个样本 $d$ 下的 $E_{d-}$
根据式6计算出期望的梯度值，和第一步获得的梯度值进行比较，它们应该几乎想等(至少4位有效数字相同)

当然，我们可以重复上面的过程，对每个权重都进行检查。也可以使用多个样本重复检查。

def gradient_check(network, sample_feature, sample_label):
    '''
    梯度检查
    network: 神经网络对象
    sample_feature: 样本的特征
    sample_label: 样本的标签
    '''
    # 计算网络误差
    network_error = lambda vec1, vec2: \
            0.5 * reduce(lambda a, b: a + b, 
                      map(lambda v: (v[0] - v[1]) * (v[0] - v[1]),
                          zip(vec1, vec2)))
    # 获取网络在当前样本下每个连接的梯度
    network.get_gradient(sample_feature, sample_label)
    # 对每个权重做梯度检查    
    for conn in network.connections.connections: 
        # 获取指定连接的梯度
        actual_gradient = conn.get_gradient()
        # 增加一个很小的值，计算网络的误差
        epsilon = 0.0001
        conn.weight += epsilon
        error1 = network_error(network.predict(sample_feature), sample_label)
        # 减去一个很小的值，计算网络的误差
        conn.weight -= 2 * epsilon # 刚才加过了一次，因此这里需要减去2倍
        error2 = network_error(network.predict(sample_feature), sample_label)
        # 根据式6计算期望的梯度值
        expected_gradient = (error2 - error1) / (2 * epsilon)
        # 打印
        print 'expected gradient: \t%f\nactual gradient: \t%f' % (
            expected_gradient, actual_gradient)

至此，会推导、会实现、会抓BUG，你已经摸到深度学习的大门了。接下来还需要不断的实践，我们用刚刚写过的神经网络去识别手写数字。

7 神经网络实战——手写数字识别

针对这个任务，我们采用业界非常流行的MNIST数据集。MNIST大约有60000个手写字母的训练样本，我们使用它训练我们的神经网络，然后再用训练好的网络去识别手写数字。

手写数字识别是个比较简单的任务，数字只可能是0-9中的一个，这是个10分类问题。

7.1 超参数的确定

我们首先需要确定网络的层数和每层的节点数。关于第一个问题，实际上并没有什么理论化的方法，大家都是根据经验来拍，如果没有经验的话就随便拍一个。然后，你可以多试几个值，训练不同层数的神经网络，看看哪个效果最好就用哪个。嗯，现在你可能明白为什么说深度学习是个手艺活了，有些手艺很让人无语，而有些手艺还是很有技术含量的。

不过，有些基本道理我们还是明白的，我们知道网络层数越多越好，也知道层数越多训练难度越大。对于全连接网络，隐藏层最好不要超过三层。那么，我们可以先试试仅有一个隐藏层的神经网络效果怎么样。毕竟模型小的话，训练起来也快些(刚开始玩模型的时候，都希望快点看到结果)。

输入层节点数是确定的。因为MNIST数据集每个训练数据是28*28的图片，共784个像素，因此，输入层节点数应该是784，每个像素对应一个输入节点。

输出层节点数也是确定的。因为是10分类，我们可以用10个节点，每个节点对应一个分类。输出层10个节点中，输出最大值的那个节点对应的分类，就是模型的预测结果。

隐藏层节点数量是不好确定的，从1到100万都可以。下面有几个经验公式：
$\begin{aligned} &m=\sqrt{n+l}+\alpha\\ &m=log_2n\\ &m=\sqrt{nl}\\ &m:隐藏层节点数\\ &n:输入层节点数\\ &l:输出层节点数\\ &\alpha:1到10之间的常数 \end{aligned}$

因此，我们可以先根据上面的公式设置一个隐藏层节点数。如果有时间，我们可以设置不同的节点数，分别训练，看看哪个效果最好就用哪个。我们先拍一个，设隐藏层节点数为300吧。

对于3层 $784 * 300 * 10$ 的全连接网络，总共有 $300 * (784 + 1) + 10 * (300 + 1) = 238510$ 个参数！神经网络之所以强大，是它提供了一种非常简单的方法去实现大量的参数。目前百亿参数、千亿样本的超大规模神经网络也是有的。因为MNIST只有6万个训练样本，参数太多了很容易过拟合，效果反而不好。

7.2 模型的训练和评估

MNIST数据集包含10000个测试样本。我们先用60000个训练样本训练我们的网络，然后再用测试样本对网络进行测试，计算识别错误率：
$错误率=\frac{错误预测样本数}{总样本数}$
我们每训练10轮，评估一次准确率。当准确率开始下降时（出现了过拟合）终止训练。

7.3 代码实现

首先，我们需要把MNIST数据集处理为神经网络能够接受的形式。MNIST训练集的文件格式可以参考官方网站，这里不在赘述。每个训练样本是一个28*28的图像，我们按照行优先，把它转化为一个784维的向量。每个标签是0-9的值，我们将其转换为一个10维的one-hot向量：如果标签值为n，我们就把向量的第n维（从0开始编号）设置为0.9，而其它维设置为0.1。例如，向量[0.1,0.1,0.9,0.1,0.1,0.1,0.1,0.1,0.1,0.1]表示值2。

下面是处理MNIST数据的代码：

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import struct
from bp import *
from datetime import datetime
# 数据加载器基类
class Loader(object):
    def __init__(self, path, count):
        '''
        初始化加载器
        path: 数据文件路径
        count: 文件中的样本个数
        '''
        self.path = path
        self.count = count
    def get_file_content(self):
        '''
        读取文件内容
        '''
        f = open(self.path, 'rb')
        content = f.read()
        f.close()
        return content
    def to_int(self, byte):
        '''
        将unsigned byte字符转换为整数
        '''
        return struct.unpack('B', byte)[0]
# 图像数据加载器
class ImageLoader(Loader):
    def get_picture(self, content, index):
        '''
        内部函数，从文件中获取图像
        '''
        start = index * 28 * 28 + 16
        picture = []
        for i in range(28):
            picture.append([])
            for j in range(28):
                picture[i].append(
                    self.to_int(content[start + i * 28 + j]))
        return picture
    def get_one_sample(self, picture):
        '''
        内部函数，将图像转化为样本的输入向量
        '''
        sample = []
        for i in range(28):
            for j in range(28):
                sample.append(picture[i][j])
        return sample
    def load(self):
        '''
        加载数据文件，获得全部样本的输入向量
        '''
        content = self.get_file_content()
        data_set = []
        for index in range(self.count):
            data_set.append(
                self.get_one_sample(
                    self.get_picture(content, index)))
        return data_set
# 标签数据加载器
class LabelLoader(Loader):
    def load(self):
        '''
        加载数据文件，获得全部样本的标签向量
        '''
        content = self.get_file_content()
        labels = []
        for index in range(self.count):
            labels.append(self.norm(content[index + 8]))
        return labels
    def norm(self, label):
        '''
        内部函数，将一个值转换为10维标签向量
        '''
        label_vec = []
        label_value = self.to_int(label)
        for i in range(10):
            if i == label_value:
                label_vec.append(0.9)
            else:
                label_vec.append(0.1)
        return label_vec
def get_training_data_set():
    '''
    获得训练数据集
    '''
    image_loader = ImageLoader('train-images-idx3-ubyte', 60000)
    label_loader = LabelLoader('train-labels-idx1-ubyte', 60000)
    return image_loader.load(), label_loader.load()
def get_test_data_set():
    '''
    获得测试数据集
    '''
    image_loader = ImageLoader('t10k-images-idx3-ubyte', 10000)
    label_loader = LabelLoader('t10k-labels-idx1-ubyte', 10000)
    return image_loader.load(), label_loader.load()

网络的输出是一个10维向量，这个向量第个(从0开始编号)元素的值最大，那么就是网络的识别结果。下面是代码实现：

def get_result(vec):
    max_value_index = 0
    max_value = 0
    for i in range(len(vec)):
        if vec[i] > max_value:
            max_value = vec[i]
            max_value_index = i
    return max_value_index

我们使用错误率来对网络进行评估，下面是代码实现：

def evaluate(network, test_data_set, test_labels):
    error = 0
    total = len(test_data_set)
    for i in range(total):
        label = get_result(test_labels[i])
        predict = get_result(network.predict(test_data_set[i]))
        if label != predict:
            error += 1
    return float(error) / float(total)

最后实现我们的训练策略：每训练10轮，评估一次准确率，当准确率开始下降时终止训练。下面是代码实现：

def train_and_evaluate():
    last_error_ratio = 1.0
    epoch = 0
    train_data_set, train_labels = get_training_data_set()
    test_data_set, test_labels = get_test_data_set()
    network = Network([784, 300, 10])
    while True:
        epoch += 1
        network.train(train_labels, train_data_set, 0.3, 1)
        print '%s epoch %d finished' % (now(), epoch)
        if epoch % 10 == 0:
            error_ratio = evaluate(network, test_data_set, test_labels)
            print '%s after epoch %d, error ratio is %f' % (now(), epoch, error_ratio)
            if error_ratio > last_error_ratio:
                break
            else:
                last_error_ratio = error_ratio
if __name__ == '__main__':
    train_and_evaluate()

在我的机器上测试了一下，1个epoch大约需要9000多秒，所以要对代码做很多的性能优化工作（比如用向量化编程）。训练要很久很久，可以把它上传到服务器上，在tmux的session里面去运行。为了防止异常终止导致前功尽弃，我们每训练10轮，就把获得参数值保存在磁盘上，以便后续可以恢复。(代码略)

8 向量化编程

完整代码请参考GitHub: https://github.com/hanbt/learn_dl/blob/master/fc.py (python2.7)

在经历了漫长的训练之后，我们可能会想到，肯定有更好的办法！是的，程序员们，现在我们需要告别面向对象编程了，转而去使用另外一种更适合深度学习算法的编程方式：向量化编程。主要有两个原因：一个是我们事实上并不需要真的去定义Node、Connection这样的对象，直接把数学计算实现了就可以了；另一个原因，是底层算法库会针对向量运算做优化（甚至有专用的硬件，比如GPU），程序效率会提升很多。所以，在深度学习的世界里，我们总会想法设法的把计算表达为向量的形式。我相信优秀的程序员不会把自己拘泥于某种（自己熟悉的）编程范式上，而会去学习并使用最为合适的范式。

下面，我们用向量化编程的方法，重新实现前面的全连接神经网络。

首先，我们需要把所有的计算都表达为向量的形式。对于全连接神经网络来说，主要有三个计算公式。

前向计算，我们发现式2已经是向量化的表达了：
$\vec{a}=\sigma(W\centerdot\vec{x})\qquad (式2)$

上式中的 $\sigma$ 表示sigmoid函数。

反向计算，我们需要把式3和式4使用向量来表示：
$\vec{\delta}=\vec{y}(1-\vec{y})(\vec{t}-\vec{y})\qquad(式7)\\ \vec{\delta^{(l)}}=\vec{a}^{(l)}(1-\vec{a}^{(l)})W^T\delta^{(l+1)}\qquad(式8)$
在式8中， $\delta^{(l)}$ 表示第l层的误差项； $W^T$ 表示矩阵 $W$ 的转置。

我们还需要权重数组W和偏置项b的梯度计算的向量化表示。也就是需要把式5使用向量化表示：
$w_{ji}\gets w_{ji}+\eta\delta_jx_{ji}\qquad(式5)$
其对应的向量化表示为：
$\gets W + \eta\vec{\delta}\vec{x}^T\qquad(式9)$
更新偏置项的向量化表示为：
$\vec{b} \gets \vec{b} + \eta\vec{\delta}\qquad(式10)$
现在，我们根据上面几个公式，重新实现一个类：FullConnectedLayer。它实现了全连接层的前向和后向计算：

# 全连接层实现类
class FullConnectedLayer(object):
    def __init__(self, input_size, output_size, 
                 activator):
        '''
        构造函数
        input_size: 本层输入向量的维度
        output_size: 本层输出向量的维度
        activator: 激活函数
        '''
        self.input_size = input_size
        self.output_size = output_size
        self.activator = activator
        # 权重数组W
        self.W = np.random.uniform(-0.1, 0.1,
            (output_size, input_size))
        # 偏置项b
        self.b = np.zeros((output_size, 1))
        # 输出向量
        self.output = np.zeros((output_size, 1))
    def forward(self, input_array):
        '''
        前向计算
        input_array: 输入向量，维度必须等于input_size
        '''
        # 式2
        self.input = input_array
        self.output = self.activator.forward(
            np.dot(self.W, input_array) + self.b)
    def backward(self, delta_array):
        '''
        反向计算W和b的梯度
        delta_array: 从上一层传递过来的误差项
        '''
        # 式8
        self.delta = self.activator.backward(self.input) * np.dot(
            self.W.T, delta_array)
        self.W_grad = np.dot(delta_array, self.input.T)
        self.b_grad = delta_array
    def update(self, learning_rate):
        '''
        使用梯度下降算法更新权重
        '''
        self.W += learning_rate * self.W_grad
        self.b += learning_rate * self.b_grad

上面这个类一举取代了原先的Layer、Node、Connection等类，不但代码更加容易理解，而且运行速度也快了几百倍。

现在，我们对Network类稍作修改，使之用到FullConnectedLayer：

# Sigmoid激活函数类
class SigmoidActivator(object):
    def forward(self, weighted_input):
        return 1.0 / (1.0 + np.exp(-weighted_input))
    def backward(self, output):
        return output * (1 - output)
# 神经网络类
class Network(object):
    def __init__(self, layers):
        '''
        构造函数
        '''
        self.layers = []
        for i in range(len(layers) - 1):
            self.layers.append(
                FullConnectedLayer(
                    layers[i], layers[i+1],
                    SigmoidActivator()
                )
            )
    def predict(self, sample):
        '''
        使用神经网络实现预测
        sample: 输入样本
        '''
        output = sample
        for layer in self.layers:
            layer.forward(output)
            output = layer.output
        return output
    def train(self, labels, data_set, rate, epoch):
        '''
        训练函数
        labels: 样本标签
        data_set: 输入样本
        rate: 学习速率
        epoch: 训练轮数
        '''
        for i in range(epoch):
            for d in range(len(data_set)):
                self.train_one_sample(labels[d], 
                    data_set[d], rate)
    def train_one_sample(self, label, sample, rate):
        self.predict(sample)
        self.calc_gradient(label)
        self.update_weight(rate)
    def calc_gradient(self, label):
        delta = self.layers[-1].activator.backward(
            self.layers[-1].output
        ) * (label - self.layers[-1].output)
        for layer in self.layers[::-1]:
            layer.backward(delta)
            delta = layer.delta
        return delta
    def update_weight(self, rate):
        for layer in self.layers:
            layer.update(rate)

现在，Network类也清爽多了，用我们的新代码再次训练一下MNIST数据集吧。

9 小结

至此，你已经完成了又一次漫长的学习之旅。你现在应该已经明白了神经网络的基本原理，高兴的话，你甚至有能力去动手实现一个，并用它解决一些问题。如果感到困难也不要气馁，这篇文章是一个重要的分水岭，如果你完全弄明白了的话，在真正的『小白』和装腔作势的『大牛』面前吹吹牛是完全没有问题的。

作为深度学习入门的系列文章，本文也是上半场的结束。在这个半场，你掌握了机器学习、神经网络的基本概念，并且有能力去动手解决一些简单的问题（例如手写数字识别，如果用传统的观点来看，其实这些问题也不简单）。而且，一旦掌握基本概念，后面的学习就容易多了。

在下半场，我们讲介绍更多『深度』学习的内容，我们已经讲了神经网络(Neutrol Network)，但是并没有讲深度神经网络(Deep Neutrol Network)。Deep会带来更加强大的能力，同时也带来更多的问题。如果不理解这些问题和它们的解决方案，也不能说你入门了『深度』学习。

目前业界有很多开源的神经网络实现，它们的功能也要强大的多，因此你并不需要事必躬亲的去实现自己的神经网络。我们在上半场不断的从头发明轮子，是为了让你明白神经网络的基本原理，这样你就能非常迅速的掌握这些工具。在下半场的文章中，我们改变了策略：不会再去从头开始去实现，而是尽可能应用现有的工具。

下一篇文章，我们介绍不同结构的神经网络，比如鼎鼎大名的卷积神经网络，它在图像和语音领域已然创造了诸多奇迹，在自然语言处理领域的研究也如火如荼。某种意义上说，它的成功大大提升了人们对于深度学习的信心。

好了，同学们累了吧，奉上美图一张，放松一下心情！

10 参考资料

Tom M. Mitchell, “机器学习”, 曾华军等译, 机械工业出版社
CS 224N / Ling 284, Neural Networks for Named Entity Recognition
LeCun et al. Gradient-Based Learning Applied to Document Recognition 1998

Godswisdom

关注

9
点赞
踩
23

收藏

觉得还不错? 一键收藏
6
评论
零基础入门深度学习(3) - 神经网络和反向传播算法

零基础入门深度学习(3) - 神经网络和反向传播算法文章目录0 文章列表1 往期回顾2 神经网络2.1 神经元2.2 神经网络是啥2.3 计算神经网络的输出2.4 神经网络的矩阵表示2.5 神经网络的训练反向传播算法(Back Propagation)2.6 反向传播算法的推导3 神经网络的实现梯度检查4 神经网络实战——手写数字识别小结参考资料无论即将到来的是大数据时代还是人工智能时代...
复制链接

扫一扫