模型选择和改进
在前几篇博客中分别介绍了线性回归,逻辑回归,神经网络的一些知识。但是,假如你想要开发一个机器学习系统或者改进一个机器系统性能的时候该怎么办?下面介绍一些方法和建议。如果你的假设函数在测试集上表现出很大的误差,那你接下来该怎么改进呢,一般会想到以下方法:

但是,有了以上方法我们该如何确定我们想要改进的机器学习系统适用于具体哪一种。盲目的选择,既浪费了时间又没有任何效果。首先要评估我们的学习算法,以便找出其中的问题,对症下药。
当我们在训练集上拟合模型时,我们希望得到使代价函数最小的参数,即使训练误差最小的参数。但是此时极容易出现过拟合的现象,导致模型的泛化能力很差。那么该如何判断我们的假设函数是过拟合呢?我们可以把原始数据集分割成训练集和测试集,一般按照7:3的比例分割,最好随机选择70%作为训练集,剩下的30%作为测试集。如下图所示:
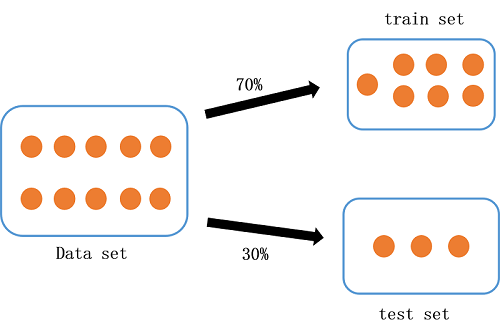
我们在训练集上最小化训练误差得到参数,使用在训练集上得到的假设函数在测试集上测试,计算测试误差。这样就可以评价我们的假设函数。
一、模型选择
我们该如何选择出一个正好拟合的模型(既不过拟合又不欠拟合)。拿最简单的线性回归举例子,在下图中我们该选择那个多项式呢?我们定义一个参数d:degree of polynomial。下图中d依次为1,2,3,...10。
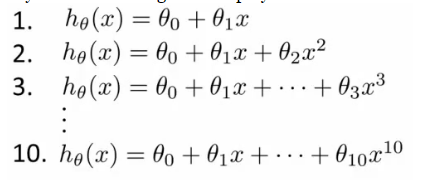
我们可以按照上面说的那样,把数据集分成训练集和测试集,在训练集上求出参数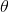 ,然后在测试集上选择测试误差最小的那个多项式。但是这个显然不合理,因为这样的话,实际上我们的参数d是和测试集拟合的,这样再去比较就不公平了。因此我们需要采用一个新的评估方法:把数据划分成训练集(train set),验证集(cross validation set),测试集(test set)。一般来说,train set占60%,CV占20%,test set占20%。因此我们可以这样评估我们的模型:在训练集上求出参数
,然后在测试集上选择测试误差最小的那个多项式。但是这个显然不合理,因为这样的话,实际上我们的参数d是和测试集拟合的,这样再去比较就不公平了。因此我们需要采用一个新的评估方法:把数据划分成训练集(train set),验证集(cross validation set),测试集(test set)。一般来说,train set占60%,CV占20%,test set占20%。因此我们可以这样评估我们的模型:在训练集上求出参数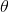 ,在验证集上找出验证误差最小的多项式,然后在测试集上评估它的泛化能力。
,在验证集上找出验证误差最小的多项式,然后在测试集上评估它的泛化能力。
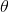 ,然后在测试集上选择测试误差最小的那个多项式。但是这个显然不合理,因为这样的话,实际上我们的参数d是和测试集拟合的,这样再去比较就不公平了。因此我们需要采用一个新的评估方法:把数据划分成训练集(train set),验证集(cross validation set),测试集(test set)。一般来说,train set占60%,CV占20%,test set占20%。因此我们可以这样评估我们的模型:在训练集上求出参数
,然后在测试集上选择测试误差最小的那个多项式。但是这个显然不合理,因为这样的话,实际上我们的参数d是和测试集拟合的,这样再去比较就不公平了。因此我们需要采用一个新的评估方法:把数据划分成训练集(train set),验证集(cross validation set),测试集(test set)。一般来说,train set占60%,CV占20%,test set占20%。因此我们可以这样评估我们的模型:在训练集上求出参数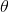 ,在验证集上找出验证误差最小的多项式,然后在测试集上评估它的泛化能力。
,在验证集上找出验证误差最小的多项式,然后在测试集上评估它的泛化能力。
二、bias vs variance (偏差vs方差)
接下来介绍两个非常重要的概念bias和variance。如果你的模型表现的不理想,基本就是两个原因:
- high bias--------under fitting problem(高偏差意味着欠拟合)
- high variance----------- over fitting problem(高方差意味着过拟合)
用个图形象的说明下high bias和high variance问题(图片来自NG machine learning课):
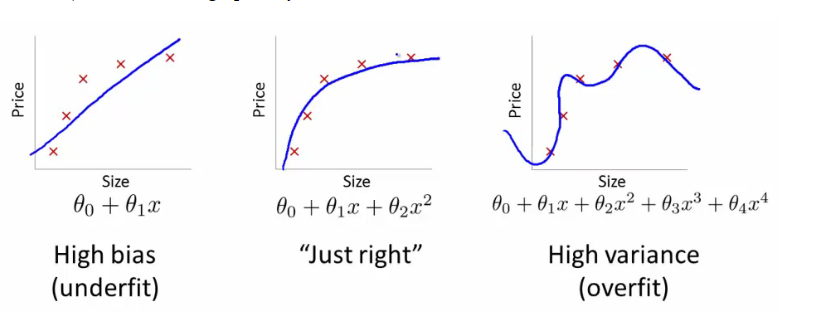
那么,我们该如何判断我们的学习算法是high bias问题还是high variance问题。我们来看个图:
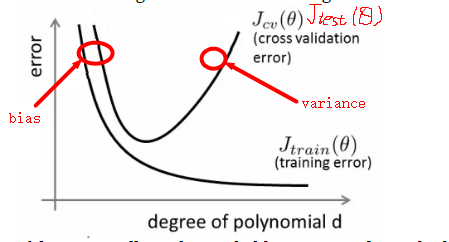
如上图所示:
- 当d很小时,可以看到训练误差和测试误差都非常大,说明此时是high bias问题。即欠拟合问题
- 当d很大时,可以看到训练误差很小,而测试误差很大,说明此时是high variance问题。即发生了过拟合。
下面我们来看看正则项是如何影响偏差和方差的。其实主要就是正则项系数 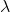 的大小是如何影响偏差和方差的。
的大小是如何影响偏差和方差的。
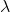 的大小是如何影响偏差和方差的。
的大小是如何影响偏差和方差的。
- 当
很大时,对应着high bias,即欠拟合。
- 当
很小时,对应着high variance,即过拟合。
用个图让大家理解下:

三、学习曲线(learning curves)
当我们想检查我们的学习算法运行是否正确,或者想看看我们希望改进算法的效果,通常使用学习曲线,即在坐标系中画出训练样本数和训练误差、测试误差的关系。我们来看看high bias和high variance时学习曲线的样子。
1、首先看看high bias的情况:
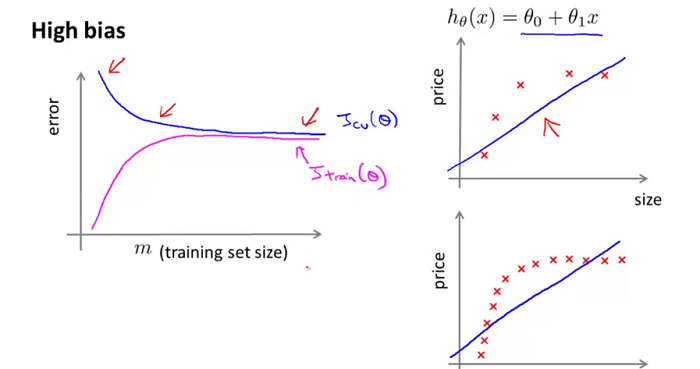
从上图我们能够发现:当学习算法处于high bias时,增加训练集样本数是没用的。
2、再来看看high variance的情况:
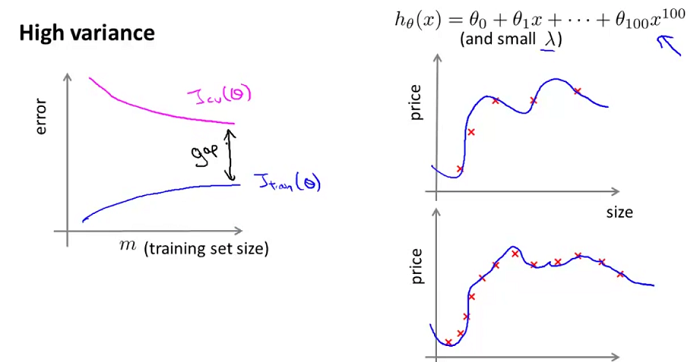
同样,从上图我们能够发现:当学习模型处于high variance时,增大训练样本数量,可能会有点帮助。
四、总结
以上就是应用机器学习算法时的advice。目的是为了让大家了解出现问题时该用什么办法应对,即把两类问题high bias和high variance,和开头的解决办法对应起来:

























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








