贝叶斯网络与隐马尔科夫模型

原文地址:贝叶斯网络与隐马尔科夫模型 转载请注明出处

如果你想了解更多机器学习算法，请关注我的AI博客

前言

贝叶斯网络是机器学习中非常经典的算法之一，它能够根据已知的条件来估算出不确定的知识，应用范围非常的广泛。贝叶斯网络以贝叶斯公式为理论接触构建成了一个有向无环图，我们可以通过贝叶斯网络构建的图清晰的根据已有信息预测未来信息。

本文将会从最基本的概率基础开始讲解，并延伸到贝叶斯网络与隐马尔科夫链。

条件概率

条件概率是指一个事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为$P(A|B)$，读作在B条件下A的概率。

$$P(AB)=P(A)P(B|A)$$

全概率公式

在讲全概率公式之前，首先要理解什么是“完备事件群”。

对于任何一个事件的所有情况有，n表示所有情况的数量

$$\sum _{i=1}^n{B}_i=1$$

如果A是未知事件，那么

$$A=\sum _{i=1}^{n}A{B}_i$$

$$P(A)=\sum _{i=1}^{n}P(A{B}_i)$$

根据条件概率有

$$P(A)=\sum _{i=1}^{n}P(B_i)P(A|B_i)$$

下面我们来看一个例子。

某地盗窃风气盛行，且偷窃者屡教不改。我们根据过往的案件记录，推断A今晚作案的概率是0.8，B今晚作案的概率是0.1，C今晚作案的概率是0.5，除此之外，还推断出A的得手率是0.1，B的得手率是1.0，C的得手率是0.5。那么，今晚村里有东西被偷的概率是多少？

通过阅读上述文字，我们大概对A、B、C三人有了一个初步的印象。首先，A的脑子可能有些问题，特别喜欢偷，但是技术相当烂。B看来是个江湖高手，一般不出手，一出手就绝不失手。C大概是追求中庸，各方面都很普通。

我们将文字描述转换为数学语言，根据作案频率可知

$$\begin{gathered} P(A)=0.8 \\ P(B)=0.1 \\ P(C)=0.5 \end{gathered}$$

将“村里有东西被偷”记为S，根据得手率可以得到

$$\begin{gathered} P(S|A)=0.1 \\ P(S|B)=1.0 \\ P(S|C)=0.5 \end{gathered}$$

根据我们上面全概率的公式，就可以求得

$$P(S)=P(A)P(S|A)+P(B)P(S|B)+P(C)P(S|C)=0.43$$

贝叶斯公式

有了前面条件概率与全概率的基础，我们现在先直接抛出贝叶斯公式：

$$P(B_i|A)=\frac{P(A{B}_i)}{P(A)}=\frac{p(B_i)P(A|B_i)}{{\sum }_{j}P(B_j)P(A|B_j)}$$

上面的例子是知道小偷各自作案的概率，求被偷的概率。问你个更有意思的问题，是哪个小偷偷的，计算每个小偷偷的概率，这就是贝叶斯公式解决的问题。

为了方便大家对应上面的公式，我们这里把小偷这个变量设为B，被偷这个事件设为A，根据贝叶斯公式有

$$P(B_1|A)=\frac{P(B_1)P(A|B_1)}{P(A)}=\frac{0.8\times 0.1}{0.43}=0.186$$

$$P(B_2|A)=\frac{P(B_2)P(A|B_2)}{P(A)}=\frac{0.1\times 1.0}{0.43}=0.232$$

$$P(B_1|A)=\frac{P(B_1)P(A|B_1)}{P(A)}=\frac{0.5\times 0.5}{0.43}=0.581$$

注意，这里的$P(A)$已在上文求过，这里不再展开，正常情况应该使用全概率公式进行求解。

贝叶斯网络

在开始贝叶斯网络之前，我们需要了解一个概念，联合分布，即一个模型中，所有事件的概率，例如，一个模型中有事件A,B,C，我们要求出A,B,C分别为0或1的概率，在只有3个事件的情况下，我们需要存储$2^3$即8种情况，如果事件较多的情况下，我们是很难存储这些数据的，概率图模型就是为了能用最便捷的方式存储联合分布，贝叶斯网络就是概率图模型的一种。

如果我们能把模型中的事件以有向无环图的方式表示出来，那么，我们就可以把联合分布的概率写成所有小的事件的概率的乘积，如下图

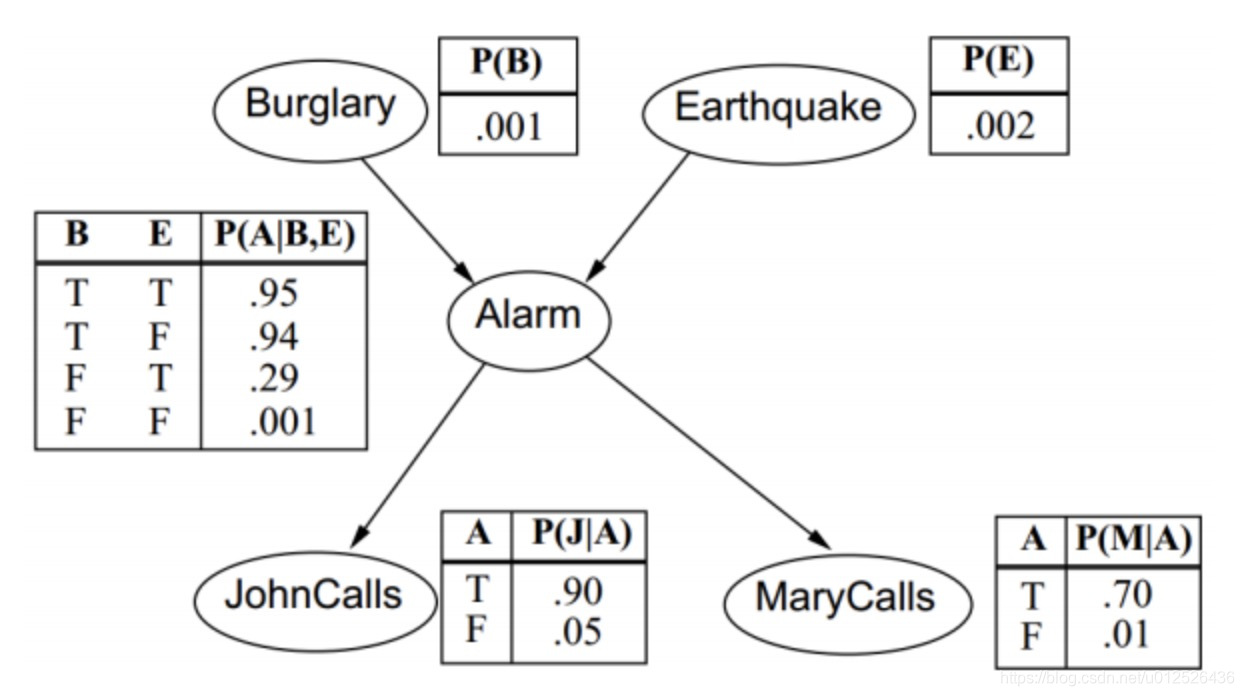
$$P(B,E,A,J,M)=P(B)P(E)P(A|B,E)P(J|A)P(M|A)$$

这里一共是5个事件，普通情况需要32个数据来存储，如果采用图模型只需要10个数据。

在一个模型中，如果我们知道所有事件的联合分布，即可知道所有事件的任何情况下的概率。例如上图给Mary打电话的概率是多少，即$P(A)$

对于求解单个事件的概率，我们可以把其他事件全部进行积分，即可求得对应的单个事件的概率，这里我们以$P(A)$为例

$$P(A)=\sum _B\sum _E\sum _M\sum _{J}P(B)P(E)P(A|B,E)P(J|A)P(M|A)$$

这里有个小技巧，因为除了$P(J|A)$中有J其他项都没有J，我们可以把J这一项单独出来，即

$$P(A)=\sum _B\sum _E\sum _{M}P(B)P(E)P(A|B,E)P(M|A)\sum _{J}P(J|A)$$

由于${\sum }_{J}P(J|A)=1$,所以我们这里就可以把这一项约掉，最终

$$P(A)=\sum _B\sum _E\sum _{M}P(B)P(E)P(A|B,E)P(M|A)$$

这里我在看一个条件概率，例如铃响那么地震的概率即$P(E|A)$，对于这样的问题，我们可以拆解成两个联合分布相除的式子

$$P(E|A)=\frac{P(EA)}{P(A)}$$

这里$P(A)$我们上面已经求出来了，对于$P(EA)$我们依旧使用积分的方法

$$P(EA)=\sum _B\sum _J\sum _{M}P(B)P(E)P(A|B,E)P(J|A)P(M|A)$$

隐马尔科夫模型 HMM

隐马尔科夫模型是概率图模型的一种特定情况，该模型存在着一种链式关系，其中，隐是表示隐含状态的意思，如下图所示，马尔科夫的意思是当前节点只与其父节点有关系，和其它节点相互独立。

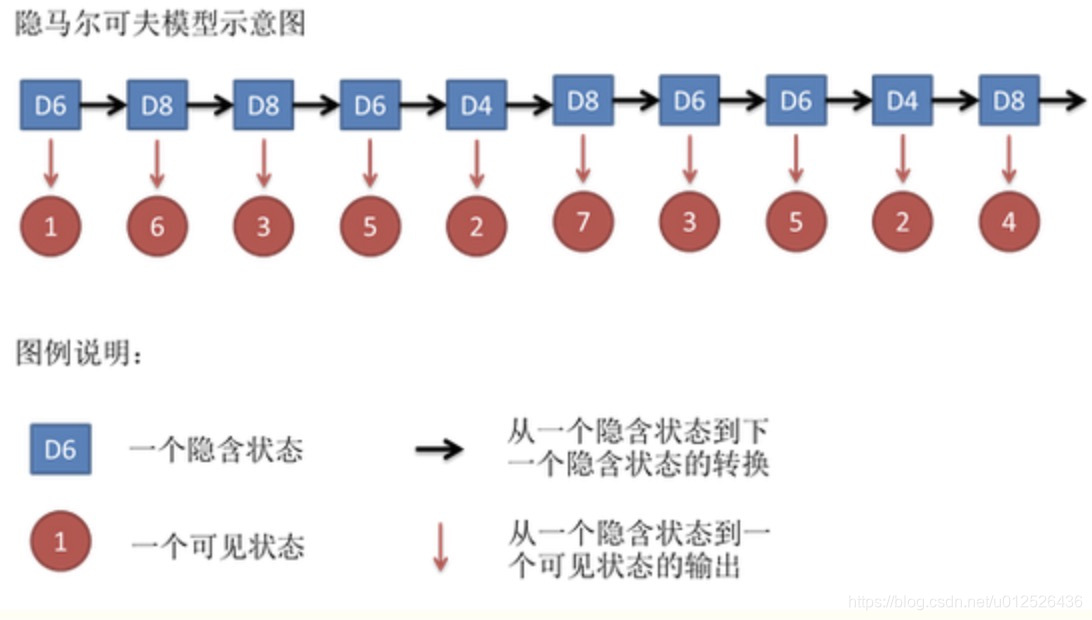
马尔科夫模型属于一个序列模型，适合用于连续性数据的场景。这里，我们以股票来举例子。

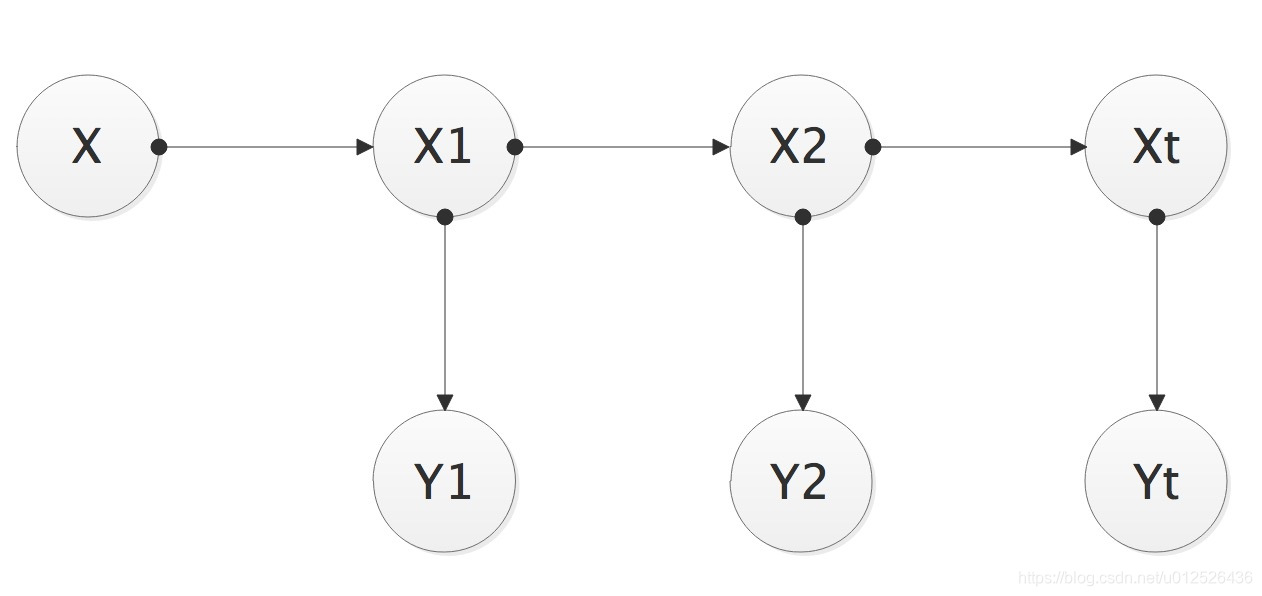
Y代表当天股票的价格，X代表股票是牛市还是熊市，我们的任务是根据$Y_1到Y_{t-1}$的数据预测$X_t$，最后拿到真正的数据$Y_t$时再更新一次$X_t$，用公式表达就是

$$P(X_t|Y_{1:t})$$

注意，这里Y的下标表示第1到t天

根据我们在贝叶斯网络中学到的内容，要求解上面的问题，首先，我们需要得到联合分布，再使用贝叶斯公式计算出其概率，接下来我们就一步一步的来把结果推导出来。

为了求最终结果，我们把计算过程分为两个大的过程

• 求 $P(X_t|Y_{1:t-1})$ 即预测过程，通过前几天的数据预测今日走势
• 求 $P(X_t|Y_{1:t})$ 即更新过程，获取今日数据之后更新走势

在求解前，我们引入一个概率公式

$$P(AB|C)=P(A|BC)P(B|C)$$

预测：

$$\begin{array}{rl}P(X_t|Y_{1:t-1})& =\sum P(X_t{X}_{1:t-1}|Y_{1:t-1})\\ & =\sum P(X_t|X_{1:t-1}{Y}_{1:t-1})P(X_{1:t-1}|Y_{1:t-1})\\ & =\sum P(X_t|X_{1:t-1})P(X_{1:t-1}|Y_{1:t-1})\end{array}$$

公式第一行使用了全概率引入了$X_{t-1}$，第二行由于$X_t$与$Y_{t-1}$没有关系，所以可以把$Y_{t-1}$约掉，最后剩余的概率值都可从联合分布中获取。

在继续一面的推断前，我们再看一下三个参数的贝叶斯公式

$$P(A|BC)=\frac{P(B|AC)P(A|C)}{P(B|C)}$$

更新：

$$\begin{array}{rl}P(X_t|Y_{1:t})& =P(X_t|Y_t{Y}_{1:t-1})\\ & =\frac{P(Y_t|X_t{Y}_{1:t-1})P(X_t|Y_{1:t-1})}{\sum P(Y_t|X_t{Y}_{1:t-1})P(X_t|Y_{1:t-1})}\\ & =\frac{P(Y_t|X_t)P(X_t|Y_{1:t-1})}{\sum P(Y_t|X_t)P(X_t|Y_{1:t-1})}\end{array}$$

公式第二行根据三参数贝叶斯公式进行变形，第三行把不相关的参数去除，剩余参数都是已知参数。

HMM模型和RNN模型很像，都是序列模型。在数据量较大的情况下，使用RNN效果较好，HMM运算过程简单，效率高，更适合轻量级的数据。