Real-Time-Rendering 矩阵的其他变换及投影矩阵（三）

        接下来我们讨论矩阵的平移、投影变换，在计算机图形学中这两种变换也及其常用。

一、4x4矩阵

        在讨论位移矩阵前，我们需要引出4x4矩阵的相关概念。

        4D向量有4个分量，前三个是标准的x、y、z分量，第四个是w，有时称为齐次坐标。

        我们可以把齐次坐标理解为更高维度的抽象。比如2D坐标系中一个点在2D的扩展坐标齐次坐标中将有无数的点对应。他的形式为(x,y,w)。对于不在w=1平面的点，我们可以通过将x、y除以w来将这个点投影到w=1的平面。所以2D坐标系中的齐次坐标(x,y,w)其实映射的实际2D点为(x/w,y/w)。3D坐标系同理。

        为什么引入4x4矩阵，第一个原因是因为方便的记法，在平移矩阵中将会讨论。第二个原因是因为w的映射性质。

二、平移矩阵

        在上一章中我们讨论的都是用3x3矩阵表示的线性变换，不包含平移。因为矩阵乘法的性质，零向量总是变化成零向量。显然无法描述分量加、减这样的平移操作。而4x4矩阵提供了数学上的技巧帮我们做到这一点。

        暂时假设w总是等于1，那么，标准3D向量[x,y,z]对应的4D向量为[x,y,z,1]。任意3x3变换矩阵在4D中表示为：

        

        

        

        可以发现中间的3x3矩阵依然可以代表线性变换改变向量的x、y、z分量，如果我们想屏蔽线性变换只需中间的3x3方阵改变为单元矩阵即可。而现在x、y、z分量同时被4x4矩阵的第四列所影响（如果矩阵以行为主，则是第四行）。只是因为我们都设为0，所以他并没有向量带来实际变换，但他却有加减的特性，利用此数学技巧我们可以利用矩阵的第四列实现向量的平移变换。

        

        当中间的3x3方阵包含一个线性变换时，外面包裹上位移矩阵的第4列，即实现了诸如y = ax + b形式的映射，我们称其为仿射变换。

        之前我们将列向量的w总是设为1，现在我们设为0，很容易发现位移矩阵的第四列失去了作用。换句话说，列向量的w可以开关平移矩阵。所以在计算变换时，向量如果代表一个点，说明他具有3D坐标系中的具体位置，我们应该把w设为1。如果向量就是作为向量，只具有方向的含义，我们应将w设为0，屏蔽无用的位置偏移的信息。

        在上一章中我们所做的线性操作要求任意轴都经过原点。现在我们有了位移矩阵就可以获得不经过原点的任意轴的仿射变换。我们可以将向量先平移至原点，在做线性变换，再将向量反向平移回去。即可实现向量对任意轴的变幻了。

        

        

        

        

三、正交矩阵

        上述混合变换时我们用到了逆矩阵，逆矩阵很好的变现了变换的逆操作，但根据第一篇矩阵的文章所述，求矩阵的逆将带来大量的运算。这里引入一种新的矩阵，正交矩阵。一个矩阵M，当且仅当矩阵M和其转置矩阵乘积等于单位矩阵。则说矩阵M正交。

        正交 <=> 

        根据矩阵第一章逆的相关定义，若矩阵乘他的逆等于单元矩阵，那么他的转置等于他的逆。

        所以如果该矩阵是正交的，那么我们在求他的逆矩阵时只需获得他的转置矩阵即可。显然转置的计算量远小于求逆的过程。

        若一个矩阵是正交的，他满足一下条件：

        1.矩阵的每一列都是单位向量。

        2.矩阵的所有列互相垂直。

        显然之前所述的旋转与镜像矩阵都是正交的。并且若一个矩阵正交，那么他的转置矩阵也正交。在计算逆矩阵中，显然如果我们知道该矩阵是正交矩阵时，直接获取其转置矩阵性能最佳。但若我们不知道他是否是正交矩阵时，先判断矩阵是否正交和直接计算矩阵逆耗费时间相同。若矩阵本来并不正交，我们只会浪费更多的计算时间。

        因为我们在矩阵的计算过程中矩阵的每一位的精度都可能超过了计算机能存储的精度。所以矩阵在浮点运算的过程中可能会累计误差，称为矩阵爬行。当我们认为一个矩阵是正交矩阵时，他可能因为外部的数据损坏或运算中的误差积累变得并不那么正交。所以有时我们需要做矩阵正交化的操作。

        施密特正交化是线性代数中标准的矩阵正交化算法。原理即每一列（行）都减去它投影于已处理过的列（行）的部分。显然得到的三个向量互相垂直。这三个向量称为3D向量空间的三个正交基。若将正交基标准化。则称为规范正交基（在线性代数中如此称呼，在3D数学基础：图形与游戏开发一书中称为标准正交基）。

        现在我们有一个3x3的矩阵，我们从矩阵中获取每一列分别记作r1，r2，r3。则求正交基的过程如下：

        

        

        

        然后将得到的三个向量标准化即可得到规范正交基。

        可以发现如果这么做正交化会出现因为选择第一个基向量的顺序的不同导致不同的结果。3D数学基础：图形与游戏开发一书中提出一个优化方法，选择一个小的因子k，每次都将一个向量减去对其余所有向量的投影，但都只减少k倍。如此迭代多次。得到的基向量会越来越正交化，但可能并不完全正交。

        

        

        

        要得到完美的结果，需要选择适当的因子k，并迭代足够次数（如10次），接着标准化即可。

四、正交投影

        一般来说，投影意味着降维操作。可以将某个方向上用零作为缩放因子。这样所有点被拉伸到平面（3D）或线（2D）中。

        如果在2D中向坐标轴投影或者在3D中向两个坐标轴形成的平面投影。我们只需将剩下的一个维度设为0即可，即上述的缩放因子设为0。得到如下矩阵：

        

        

        

        

        

        向任意直线或平面投影，位移部分用上述方法即可获取，现在我们关注经过原点的直线或平面的投影。

        上一章中获得的对任意经过原点的直线或平面的缩放矩阵，将缩放因子设为0即可获得。将0带入缩放矩阵很容易得到：

        

        

五、透视投影

        之前我们说引入齐次坐标作为4D向量的第四个分量的第二个原因是w可以为其他坐标做除以w的操作。这个性质在透视投影中得到运用。

        之前的平行投影之所以成为平行投影是因为投影线互相平行。而3D中透视投影的投影线不在平行，且会相交于一点，该点成为投影中心。

        透视投影是人类视觉系统的模型，充分显示出小孔成像的几何特性。

        而图形接口如OpenGL中的投影矩阵与小孔成像相比只是在光透过小孔前就会成像。且一般都会投影到摄像机的z = 近裁剪面形成的平行于xy平面的面上。如下图所示。

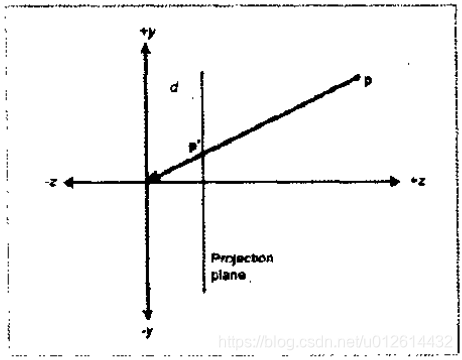
        我们现在将点P投影到P'。设P点的z分量为z。投影面的z分量即P'点的z分量为d。投影公式为：

        

        

        我们将P'转换为带有w的4D坐标即。是的4D坐标中x、y、z坐标分别除以w等于前面的3D坐标的x、y、z。

        所以我们需要构造一个4x4矩阵完成上述映射。矩阵如下：

        

        当然真正使用的投影矩阵比这个复杂的多，比如unity中将摄像机坐标系下的点变换为投影坐标系下的点所使用的矩阵。在下一章中我们会详细讲述。