离散周期信号傅里叶级数 — Fourier Series of Discrete-Time Periodic Signals

连续信号通常是数学领域里的理论研究对象，而现实生活中我们遇到的信号往往是离散的，且计算机只能处理有限长度的离散信号。所以为了让傅立叶分析解决实际问题，有必要将其推广到离散信号领域。【阅读本文前，建议先了解连续周期信号傅里叶级数】

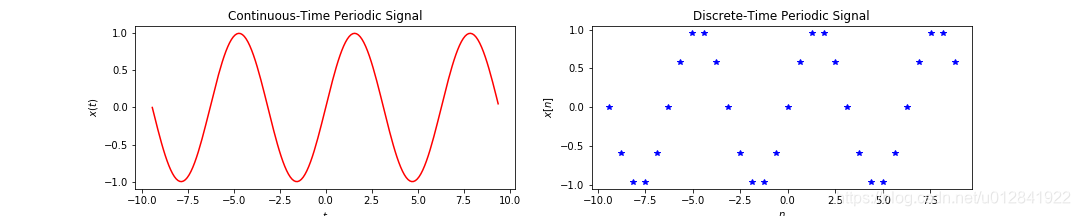
连续周期信号和离散周期信号如上图：左图为连续周期正弦波$x(t)=x(t+T)$，其中周期$T=2\pi$；右图为左图正弦波的周期离散采样，$x[n]=x[n+N]$，其中周期$N=10$。

和连续周期信号傅立叶级数基于一样的猜想，离散周期信号傅立叶级数是想寻得一组不同振幅、不同频率和不同相位的正弦离散函数以表达某离散周期信号。即：
$$x[n]=C+\sum _{k=1}^{\infty }{a}_k\sin (k{w}_{0}n)+\sum _{k=1}^{\infty }{b}_k\cos (k{w}_{0}n)$$

其中$w_0=\frac{2\pi }{N}$。根据欧拉公式$e^{ix}=\cos (x)+i\sin (x)$得：
$$\{\begin{array}{l}\cos (x)=\frac{e^{ix}+e^{-ix}}{2}\\ \sin (x)=\frac{e^{ix}-e^{-ix}}{2i}\end{array}$$

因此，上式可推导为：
$$\begin{array}{rl}& x[n]=C+\sum _{k=1}^{\infty }(a_k\frac{e^{ik{w}_{0}n}-e^{-ik{w}_{0}n}}{2i}+b_k\frac{e^{ik{w}_{0}n}+e^{-ik{w}_{0}n}}{2})\\ & =C+\sum _{k=1}^{\infty }(\frac{i{a}_k-b_k}{2}{e}^{ik{w}_{0}n}+\frac{-i{a}_k-b_k}{2}{e}^{-ik{w}_{0}n})\end{array}$$

令$A_k=\frac{i{a}_k-b_k}{2}$和$B_k=\frac{-i{a}_k-b_k}{2}$，得到$x[n]的傅立叶级数复数形式的表达式$：
$$\begin{array}{rl}& x[n]=C{e}^{i0w_{0}n}+\sum _{k=1}^{\infty }{A}_k{e}^{ik{w}_{0}n}+\sum _{k=1}^{\infty }{B}_k{e}^{-ik{w}_{0}n}\\ & =\sum _{k=-1}^{-\infty }{B}_{-k}{e}^{ik{w}_{0}n}+C{e}^{i0w_{0}n}+\sum _{k=1}^{\infty }{A}_k{e}^{ik{w}_{0}n}\\ & =\sum _{k=-\infty }^{\infty }{D}_k{e}^{ik{w}_{0}n}\end{array}$$

我们接着观察该级数中的单项$e^{ik{w}_{0}n}$：
$${\varphi }_k[n]=e^{ik{w}_{0}n}=e^{ik\frac{2\pi }{N}n},n=0,\pm 1,\pm 2,\dots$$
先说结论：${\varphi }_k[n]={\varphi }_{k+rN}[n]$，其中$k=0,\pm 1,\pm 2,\dots$、$r=0,1,2,\dots$、$N$为离散信号$x[n]$的变化周期。证明过程如下：
$$\begin{array}{rl}& {\varphi }_{k+rN}[n]=e^{i(k+rN)\frac{2\pi }{N}n}=e^{ik\frac{2\pi }{N}n}{e}^{ir2\pi n}=e^{ik\frac{2\pi }{N}n}(e^{i2\pi }{)}^{rn}\\ & =e^{ik\frac{2\pi }{N}n}(\cos (2\pi )+i\sin (2\pi ){)}^{rn}\\ & =e^{ik\frac{2\pi }{N}n}(1{)}^{rn}\\ & =e^{ik\frac{2\pi }{N}n}={\varphi }_k[n]\end{array}$$

因此，得到离散周期信号$x[n]$的傅立叶级数如下：
$$x[n]=\sum _{k=<N>}{X}_k{e}^{ik\frac{2\pi }{N}n}$$

给出： $$\sum _{n=<N>}{e}^{ik\frac{2\pi }{N}n}=\{\begin{array}{ll}N,& k=0,\pm N,\pm 2N,\dots \\ 0,& otherwise\end{array}$$ 令$S={\sum }_{n=<N>}^{}{e}^{ik\frac{2\pi }{N}n}$，证明过程如下： $$S(1^{\frac{k}{N}}-1)=e^{ik\frac{2\pi }{N}}S-S=e^{ik\frac{2\pi }{N}N}-e^{ik\frac{2\pi }{N}0}=e^{ik2\pi }-1=1^k-1=0$$ 由上式可知，当$k̸=0,\pm N,\pm 2N,\dots$时： $$(1^{\frac{k}{N}}-1)̸=0且S=\sum _{n=<N>}{e}^{ik\frac{2\pi }{N}n}=0$$ 当$k=0,\pm N,\pm 2N,\dots$时： $$S=\sum _{n=<N>}{e}^{ik\frac{2\pi }{N}n}=\sum _{n=<N>}(e^{i2\pi }{)}^{\frac{k}{N}n}=\sum _{n=<N>}(1{)}^{rn}=N,r=0,\pm 1,\pm 2,\dots$$

现在，对离散周期信号$x[n]$每时刻的信号求和，并乘以$e^{-ir\frac{2\pi }{N}n}$得：
$$\sum _{n=<N>}x[n]e^{-ir\frac{2\pi }{N}n}=\sum _{n=<N>}\sum _{k=<N>}{X}_k{e}^{i(k-r)\frac{2\pi }{N}n}=\sum _{k=<N>}{X}_k\sum _{n=<N>}{e}^{i(k-r)\frac{2\pi }{N}n}$$

由上面给出的公式可以得出，当$k-r=0$时，${\sum }_{n=<N>}^{}{e}^{i(k-r)\frac{2\pi }{N}n}=N$；当$k-r̸=0$时，${\sum }_{n=<N>}^{}{e}^{i(k-r)\frac{2\pi }{N}n}=0$。所以：
$$\sum _{n=<N>}x[n]e^{-ir\frac{2\pi }{N}n}=\sum _{k=<N>}{X}_k\sum _{n=<N>}{e}^{i(k-r)\frac{2\pi }{N}n}=X_{r}N$$

即：
$$X_r=\frac{1}{N}\sum _{n=<N>}x[n]e^{-ir\frac{2\pi }{N}n}$$

至此，我们已经得到离散周期信号$x[n]$的傅立叶级数（如下）：
$$x[n]=\sum _{k=<N>}{X}_k{e}^{ik\frac{2\pi }{N}n}$$

其中，$X_k=\frac{1}{N}{\sum }_{n=<N>}^{}x[n]e^{-ik\frac{2\pi }{N}n}$。