HDU 4419 Colourful Rectangle (线段树扫描线)

http://acm.hdu.edu.cn/showproblem.php?pid=4419

Colourful Rectangle
Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1272    Accepted Submission(s): 504

Problem Description

We use Red, Green and Blue to make new colours. See the picture below:


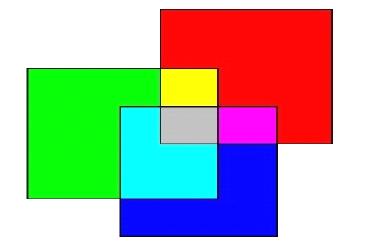
Now give you n rectangles, the colour of them is red or green or blue. You have calculate the area of 7 different colour. (Note: A region may be covered by same colour several times, but it’s final colour depends on the kinds of different colour)

 

Input

The first line is an integer T(T <= 10), the number of test cases. The first line of each case contains a integer n (0 < n <= 10000), the number of rectangles. Then n lines follows. Each line start with a letter C(R means Red, G means Green, B means Blue) and four integers x1, y1, x2, y2(0 <= x1 < x2 < 10^9, 0 <= y1 < y2 < 10^9), the left-bottom's coordinate and the right-top's coordinate of a rectangle.

 

Output

For each case, output a line "Case a:", a is the case number starting from 1,then 7 lines, each line contain a integer, the area of each colour. (Note: You should print the areas as the order: R, G, B, RG, RB, GB, RGB).

 

Sample Input

  
  

   
   3
2
R 0 0 2 2
G 1 1 3 3 
3
R 0 0 4 4
G 2 0 6 4
B 0 2 6 6
3
G 2 0 3 8
G 1 0 6 1
B 4 2 7 7
  
  

 

Sample Output

  
  

   
   Case 1:
3
3
0
1
0
0
0
Case 2:
4
4
12
4
4
4
4
Case 3:
0
12
15
0
0
0
0
  
  

 

Source

2012 ACM/ICPC Asia Regional Hangzhou Online

 

题意：

给出R，G，B三种颜色的矩形的数据，求最后7种颜色(R,G,B,RG,RB,GB,RGB)的面积是多少？

分析：

显然的线段树扫描线，可以说这题非常考验对线段树扫描线的理解，如果只会用模板，恐怕很难做出来。

R，G，B三种颜色最后会产生7种颜色(无色不算)，可以预见本题对编码质量要求相当之高。

update()操作和一般的线段树扫描线并无太大的不同，本题的精髓在于query()！

一般的简单扫描线甚至不用写query，因为根结点维护的区间覆盖长度就是我们所需要的。但是本题需要从复杂的信息中分出7种信息！显然根结点不能直接拿来用。

什么样的信息是我们需要的呢？如果我们能确定一个区间(结点)的颜色，那么该区间(结点)的信息就是我们所需要的，否则我们应继续查询他的左右儿子。那么如何确定一个区间(结点)的颜色呢？显然如果R，G，B三色要么能覆盖整个区间或不在这个区间（见我代码中的judge()函数），那么该区间的颜色就能确定！然后再计算该区间(结点)的有用信息（_plus()函数）。

如果仅仅如此，依然只是套模板的水平。本题与一般的线段树扫描线的不同之处在于查询时需要向下传递信息（pushdown()函数）！为什么？比如在[3,7)区间内，R覆盖了[3,7)这一条,G覆盖了[5,7)这一条，当我们查询到[3,7)时，并不能确定该区间(结点)的颜色，所以我们就要查询它的左右儿子。但如果直接查询，可能会丢失一部分我们需要的信息，比如[3,7)的R，如果不下传，这条线段的信息就会被丢失！当然，我们查询过后需要恢复下传的信息（recover()函数），否则会出现信息的重复，导致最终无法把线段删除干净。

/*
 *
 *  Author  :  fcbruce
 *
 *  Date  :  2014-09-23 23:34:34 
 *
 */
#include <cstdio>
#include <iostream>
#include <sstream>
#include <cstdlib>
#include <algorithm>
#include <ctime>
#include <cctype>
#include <cmath>
#include <string>
#include <cstring>
#include <stack>
#include <queue>
#include <list>
#include <vector>
#include <map>
#include <set>
#define sqr(x) ((x)*(x))
#define LL long long
#define itn int
#define INF 0x3f3f3f3f
#define PI 3.1415926535897932384626
#define eps 1e-10

#ifdef _WIN32
  #define lld "%I64d"
#else
  #define lld "%lld"
#endif

#define maxm 
#define maxn 10007

using namespace std;

long long l_r,l_g,l_b,l_rg,l_rb,l_gb,l_rgb;

struct __seg
{
  int l,r,h,type,col;
  bool operator < (const __seg &s)const
  {
    return h<s.h;
  }
}seg[maxn<<1];

int X[maxn<<1];

int sum_r[maxn<<2],sum_g[maxn<<2],sum_b[maxn<<2];
int col_r[maxn<<2],col_g[maxn<<2],col_b[maxn<<2];

inline void
pushup(int k,int l,int r)
{
  int lc=k*2+1,rc=k*2+2;
  
  sum_r[k]=sum_g[k]=sum_b[k]=0;
  
  if (r-l>1)
  {
    sum_r[k]=sum_r[lc]+sum_r[rc];
    sum_g[k]=sum_g[lc]+sum_g[rc];
    sum_b[k]=sum_b[lc]+sum_b[rc];
  }
  
  if (col_r[k]>0) sum_r[k]=X[r]-X[l];
  if (col_g[k]>0) sum_g[k]=X[r]-X[l];
  if (col_b[k]>0) sum_b[k]=X[r]-X[l];
}

void
update(int a,int b,int col,int v,int k,int l,int r)
{
  if (b<=l || r<=a) return ;
  if (a<=l && r<=b)
  {
    switch(col)
    {
      case 1:col_r[k]+=v;break;
      case 2:col_g[k]+=v;break;
      case 3:col_b[k]+=v;break;
    }
    pushup(k,l,r);

    return ;
  }
  
  update(a,b,col,v,k*2+1,l,l+r>>1);
  update(a,b,col,v,k*2+2,l+r>>1,r);
  
  pushup(k,l,r);
}

inline bool
judge(int k,int l,int r)
{
  return (sum_r[k]==X[r]-X[l] || sum_r[k]==0) && 
         (sum_g[k]==X[r]-X[l] || sum_g[k]==0) && 
         (sum_b[k]==X[r]-X[l] || sum_b[k]==0);
}

inline void
_plus(int k,int l,int r)
{
  int type=0;
  if (sum_r[k]==X[r]-X[l]) type|=1<<0;
  if (sum_g[k]==X[r]-X[l]) type|=1<<1;
  if (sum_b[k]==X[r]-X[l]) type|=1<<2;

  switch (type)
  {
    case 0:
      break;
    case 1:
      l_r+=X[r]-X[l];
      break;
    case 2:
      l_g+=X[r]-X[l];
      break;
    case 3:
      l_rg+=X[r]-X[l];
      break;
    case 4:
      l_b+=X[r]-X[l];
      break;
    case 5:
      l_rb+=X[r]-X[l];
      break;
    case 6:
      l_gb+=X[r]-X[l];
      break;
    case 7:
      l_rgb+=X[r]-X[l];
      break;
  }
}

inline void
pushdown(int k,int l,int r)
{
  int lc=k*2+1,rc=k*2+2,m=l+r>>1;
  
  col_r[lc]+=col_r[k];
  col_r[rc]+=col_r[k];

  col_g[lc]+=col_g[k];
  col_g[rc]+=col_g[k];

  col_b[lc]+=col_b[k];
  col_b[rc]+=col_b[k];
    
  pushup(lc,l,m);
  pushup(rc,m,r);
}

inline void
recover(int k,int l,int r)
{
  int lc=k*2+1,rc=k*2+2,m=l+r>>1;
  
  col_r[lc]-=col_r[k];
  col_r[rc]-=col_r[k];

  col_g[lc]-=col_g[k];
  col_g[rc]-=col_g[k];

  col_b[lc]-=col_b[k];
  col_b[rc]-=col_b[k];
  
  pushup(lc,l,m);
  pushup(rc,m,r);
}

void
query(int k,int l,int r)
{  
  if (judge(k,l,r))
  {
    _plus(k,l,r);
    return ;
  }
  
  pushdown(k,l,r);
  
  query(k*2+1,l,l+r>>1);
  query(k*2+2,l+r>>1,r);
  
  recover(k,l,r);
}

int
main()
{
#ifdef FCBRUCE
  freopen("/home/fcbruce/code/t","r",stdin);
#endif // FCBRUCE
  
  int T_T,__=0;
  scanf("%d",&T_T);
  
  while (T_T--)
  {
    int n;
    scanf("%d",&n);
    char _col;
    int x1,y1,x2,y2;
    int cnt=0,xn=0,col;
    for (int i=0;i<n;i++)
    {
      scanf(" %c%d%d%d%d",&_col,&x1,&y1,&x2,&y2);
      switch (_col)
      {
        case 'R':
          col=1;
          break;
        case 'G':
          col=2;
          break;
        case 'B':
          col=3;
          break;
      }
      seg[cnt++]=(__seg){x1,x2,y1,1,col};
      seg[cnt++]=(__seg){x1,x2,y2,-1,col};
      X[xn++]=x1;
      X[xn++]=x2;
    }
    
    sort(seg,seg+cnt);
    
    sort(X,X+xn);
    xn=unique(X,X+xn)-X;
    xn--;
    
    int last=0;
    long long a_r,a_g,a_b,a_rg,a_rb,a_gb,a_rgb;
    a_r=a_g=a_b=a_rg=a_rb=a_gb=a_rgb=0;
    
    memset(sum_r,0,sizeof sum_r);
    memset(sum_g,0,sizeof sum_g);
    memset(sum_b,0,sizeof sum_b);
    memset(col_r,0,sizeof col_r);
    memset(col_g,0,sizeof col_g);
    memset(col_b,0,sizeof col_b);
    
    for (int i=0;i<cnt;i++)
    {
      int a=lower_bound(X,X+xn,seg[i].l)-X;
      int b=lower_bound(X,X+xn,seg[i].r)-X;
      int col=seg[i].col,v=seg[i].type;
      
      l_r=l_g=l_b=l_rg=l_rb=l_gb=l_rgb=0;
      
      query(0,0,xn);
      
      a_r+=l_r*(seg[i].h-last);
      a_g+=l_g*(seg[i].h-last);
      a_b+=l_b*(seg[i].h-last);
      a_rg+=l_rg*(seg[i].h-last);
      a_rb+=l_rb*(seg[i].h-last);
      a_gb+=l_gb*(seg[i].h-last);
      a_rgb+=l_rgb*(seg[i].h-last);
      
      last=seg[i].h;
      
      update(a,b,col,v,0,0,xn);
    }
    
    printf("Case %d:\n",++__);
    
    printf(lld "\n",a_r);
    printf(lld "\n",a_g);
    printf(lld "\n",a_b);
    printf(lld "\n",a_rg);
    printf(lld "\n",a_rb);
    printf(lld "\n",a_gb);
    printf(lld "\n",a_rgb);
  }
  
  return 0;
}