统计学习-SVM支持向量机

SVM（support vector machine）

是机器学习中比较普及的一种线性分类器。我们知道，学习机器（就是训练得到的分类器对事物进行分类）的实际风险由经验风险和置信范围两部分组成。所谓经验风险，就是对训练数据进行学习得到的训练误差，所谓置信范围就是训练结果的适用范围。单纯看重经验风险会产生过拟合现象，也就是训练误差很小但是测试误差很大。
SVM是以训练误差作为优化问题的约束条件，以置信范围最小化作为优化目标。这句话怎么理解，先看一下SVM最终的优化问题数学表达式：

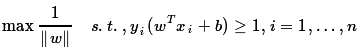
1.约束条件$y_i(w^Tx_i+b)\geq1$,也就是函数间隔大于等于1，可以理解为以训练误差为约束条件；
2.优化目标是最大化支持向量间的几何间隔；为什么说$\frac{1}{||w||}$是几何间隔？
假设存在超平面$(w,b)$，那么样本点$(x_i,y_i)$到超平面的距离为：
$\gamma_i=\frac{y_i(w^Tx_i+b)}{||w||}$
$\gamma=min\ \gamma_i$
按照最大间隔分割超平面的定义，我们可以将SVM表示为如下问题：
$max\ \gamma$
$s.t\ \gamma_i\geq\gamma,i=1,2,...N$
而我们知道同时扩大一倍$w和b$,超平面不发生改变，但是$y_i(w^Tx_i+b)$却增大一倍；再者我们知道几何距离$\gamma=\frac{函数距离}{||w||}$，故通过设定几何间隔最小的样本点对应的函数距离=1，我们可以将上面的问题可以转换为：
$max\ \frac{1}{||w||}$
$s.t \ y_i(w^Tx_i+b)\geq1$
最后为了求解方便，我们一般将问题表述如下：
$max\ \frac{1}{2}||w||^2$
$s.t \ y_i(w^Tx_i+b)\geq1$

两个概念

1. 支持向量：距离最优分类平面最近的训练点，称之为支持向量。这些点非常重要，因为支持向量可以确定最优的分类界面，同时，当找到支持向量后，非支持向量这些点就没有意义了，因为他们的存在对于分类界面没有影响，这样就会节省存储，方便计算。
2. 最优分类界面：前面已经说明了，最优分类界面完全由支持向量决定。所谓最优分类界面，就是从一系列的分类界面中，计算每个分类界面中支持向量到分类界面的距离，距离最大对应的分类界面为最优分类界面。

如何解决线性不可分的情况

线性分类器无法解决非线性可分的情况，最典型的就是异或问题，所谓抑或问题就是特征相同的样本标记为１，特征不完全相同的样本标记为０。比如（０，１）和（１，０）就可以标记为０，而（１，１）和（０，０）就可以标记为１：

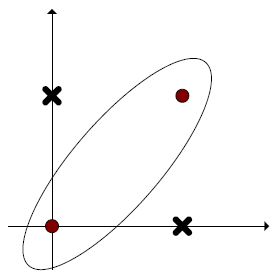
之所以说其线性不可分，一方面可以直接从感官上得到结论，你无法在二维空间找到一条直线将其有效分类，另外我们也可以假设存在$wx+b$的直线可以将其分离开，然后带入坐标点我们便会发现矛盾。
对于这类问题，我们可以将原始的训练点映射到高维空间，然后在高维空间构造线性判别函数。比如我们想把下面的红蓝点分开，很难在二维空间找到一条直线将其分开，但是如果我们令$z_1={x_1}^2,z_2={x_2}^2,z_3=x_1*x_2$，将其映射为三维点集，那么就可以将其分开。


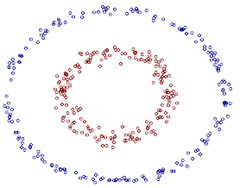
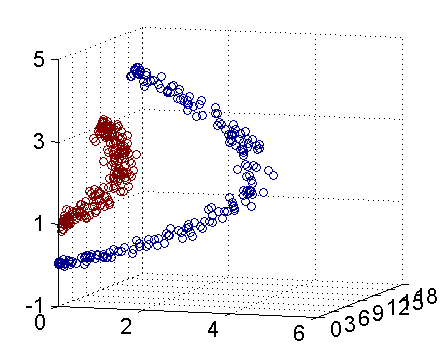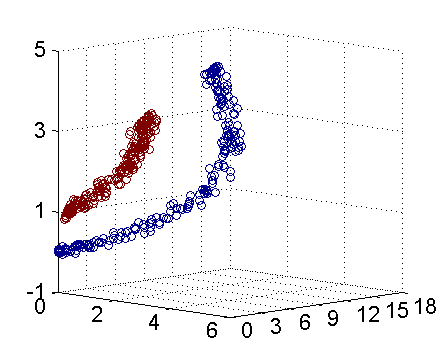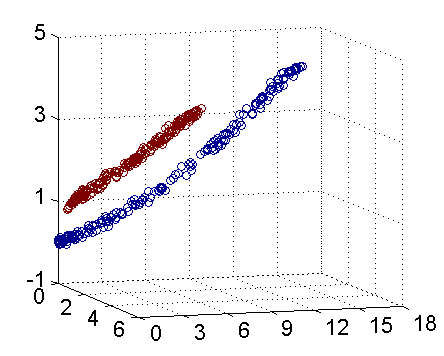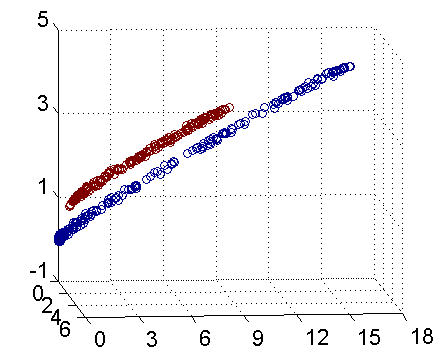
但是这种方法存在局限性，首先原始点集较大时会产生维数灾难，再者对于不同的问题我们很难确定其阶数，也就很难对应的非线性映射方式。

聪明的人发现，SVM最后优化的实际上就是一个带约束的二次规划，是一个凸优化问题（凸问题就是指的不会有局部最优解），这个优化问题可以用拉格朗日乘子法去解，使用了KKT条件的理论，这里直接作出这个式子的拉格朗日目标函数：

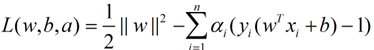
进而可以求解其对偶问题，我们可以得到（第二个式子有点问题，应该对偏置$b$的导数）：

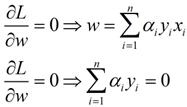
带入可得：

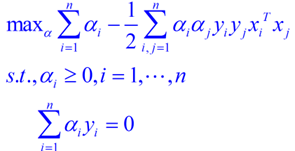
补充：
上面在进行由拉格朗日乘子法的时候，其实利用了拉格朗日的对偶性，原始问题$min_{w,b} max_\alpha{L(w,b,\alpha})$,那么原始问题的对偶问题就是$max_{\alpha} min_{w,b}{L(w,b,\alpha})$,而$min_{w,b}{L(w,b,\alpha}$便是需要求解拉格朗日函数$L(w,b,\alpha)$分别对$w,b$的偏导数

让我们先来看看推导过程中得到的一些有趣的形式。首先就是关于我们的 hyper plane 对于一个数据点$x$进行分类，实际上是通过把带入到$f(x)=w^Tx+b$算出结果然后根据其正负号来进行类别划分的。而前面的推导中我们得到 $w=\sum_{i}^{n}{\alpha}_iy_ix_i$因此

$$\begin{align} f(x)&=\left(\sum_{i=1}^n\alpha_i y_i x_i\right)^Tx+b \\ &= \sum_{i=1}^n\alpha_i y_i \langle x_i, x\rangle + b \end{align}$$

这里的形式的有趣之处在于，对于新点$x$的预测，只需要计算它与训练数据点的内积即可，这一点至关重要，是之后使用 Kernel 进行非线性推广的基本前提。此外，所谓 Supporting Vector 也在这里显示出来——事实上，所有非 Supporting Vector 所对应的系数$\alpha$都是等于零的，因此对于新点的内积计算实际上只要针对少量的“支持向量”而不是所有的训练数据即可。

我们知道对于线性不可分的情况，我们会利用一个映射将数据从低纬度映射到高纬度，假设在高维的分割超平面是

$$\begin{align} g(x)&=\left(\sum_{i=1}^n\alpha_i y_i {x_i}'\right)^Tx'+b \\ &= \sum_{i=1}^n\alpha_i y_i \langle {x_i}', x'\rangle + b \end{align}$$

那么我们不需要求解${x_i}'$和$x'$,只需要求解$\langle {x_i}', x'\rangle$，而我们可以利用核函数的性质$\langle {x_i}', x'\rangle=K({x_i}, x)$.所以在SVM的求解过程中，我们遇到内积计算的就可以利用对应的核函数进行计算，从而将低维的数据映射到高维空间，避免了显示获取由低维空间映射到高维空间的映射函数。

核函数

在选取核函数解决实际问题时，通常采用的方法有：一是利用专家的先验知识预先选定核函数；二是采用Cross-Validation方法，即在进行核函数选取时，分别试用不同的核函数，归纳误差最小的核函数就是最好的核函数．如针对傅立叶核、RBF核，结合信号处理问题中的函数回归问题，通过仿真实验，对比分析了在相同数据条件下，采用傅立叶核的SVM要比采用RBF核的SVM误差小很多．三是采用由Smits等人提出的混合核函数方法，该方法较之前两者是目前选取核函数的主流方法，也是关于如何构造核函数的又一开创性的工作．将不同的核函数结合起来后会有更好的特性，这是混合核函数方法的基本思想．。常用核函数如下：

序列最小最优化算法

通过上面的分析，我们知道SVM的学习问题可以形式化为求解凸二次规划问题，这样的凸二次规划问题具有全局最优解，并且许多优化算法可以求解这一问题，但是当训练样本很大时，这些算法往往变得很低效。而SMO（sequential minimal optimization），该算法1998年由Platt提出。
SMO是一种启发式算法，基本思想如果所有变量都满足此优化问题的KKT条件，那么我们就已经获得最优解了；否则选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题，这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解，因为这会使得原始二次规划问题的目标函数值变小。更重要的是，该子问题可以通过解析方法求解，这样可以大大提高算法的计算速度。自问题有两个变量，一个是违反KKT条件最严重的那一个，另一个是右约束条件自动确定的。如此，SMO算法将原问题不断分解为子问题，并对子问题求解，从而逐个变量的优化获得全局最优解。

参考网址：
1.核函数的定义和作用是什么？（知乎）
2.为何需要核函数？（百度文库）
3.支持向量机: Support Vector（by puskid）
4.支持向量机(SVM)基础
5.拉格朗日 SVM KKT