一般线性最小二乘法

转自：http://blog.csdn.net/u013007900/article/details/45933435

最小二乘法：

人们对由某一变量t 或多个变量 t1,…,tn  构成的相关变量 y 感兴趣。如弹簧的形变与所用的力相关，一个企业的盈利与其营业额，投资收益和原始资本有关。为了得到这些变量同y之间的关系，便用不相关变量去构建y，使用如下函数模型 

ym=f(t1,…,tq;x1,…,xp)

q个相关变量或p个附加的相关变量去拟和。 
通常人们将一个可能的、对不相关变量t的构成都无困难的函数类型称作函数模型（如抛物线函数或指数函数）。参数x是为了使所选择的函数模型同观测值y相匹配。（如在测量弹簧形变时，必须将所用的力与弹簧的膨胀系数联系起来）。其目标是合适地选择参数，使函数模型最好的拟合观测值。一般情况下，观测值远多于所选择的参数。 
其次的问题是怎样判断不同拟合的质量。高斯和勒让德的方法是，假设测量误差的平均值为0。令每一个测量误差对应一个变量并与其它测量误差不相关（随机无关）。人们假设，在测量误差中绝对不含系统误差，它们应该是纯偶然误差，围绕真值波动。除此之外，测量误差符合正态分布，这保证了偏差值在最后的结果y上忽略不计。 
确定拟合的标准应该被重视，并小心选择，较大误差的测量值应被赋予较小的权。并建立如下规则：被选择的参数，应该使算出的函数曲线与观测值之差的平方和最小。用函数表示为： 

minx⃗ ∑i=1n(ym−yi)2

用欧几里得度量表达为： 

minx⃗ ∥y⃗ m(x⃗ )−y⃗ ∥2 

最小化问题的精度，依赖于所选择的函数模型。

线性函数模型

典型的一类函数模型是线性函数模型。最简单的线性式是 y=x0+x1t ，写成行列式，为 

minx0,x1∥∥∥∥∥⎛⎝⎜⎜1⋮1t1⋮tn⎞⎠⎟⎟(x0x1)−⎛⎝⎜⎜y1⋮yn⎞⎠⎟⎟∥∥∥∥∥2=minx∥Ax−b∥2

直接给出该式的参数解： 

x1=∑ni=1tiyi−n⋅t¯y¯∑ni=1t2i−n⋅(t¯)2和x0=y¯−x1t¯

其中 t¯=1n∑ni=1ti ，为 t 值的算术平均值。也可解得如下形式： 

x1=∑ni=1(ti−t¯)(yi−y¯)∑ni=1(ti−t¯)2

一般线性情况

若含有更多不相关模型变量 t1,...,tq ，可如组成线性函数的形式 
y(t1,…,tq;x0,x1,…,xq)=x0+x1t1+⋯+xqtq  
即线性方程组 

x0+x1t11+⋯+xjt1j+⋯+xqt1q=y1x0+x1t21+⋯+xjt2j+⋯+xqt2q=y2⋮x0+x1ti1+⋯+xjtij+⋯+xqtiq=yi⋮x0+x1tn1+⋯+xjtnj+⋯+xqtnq=yn

通常人们将tij记作数据矩阵 A，参数xj记做参数矢量x，观测值yi记作b，则线性方程组又可写成： 

⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜11⋮1⋮1t11t21ti1tn1⋯⋯⋯⋯t1j⋯t2j⋯tij⋯tnj⋯t1qt2qtiqtnq⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⋅⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜x0x1x2⋮xj⋮xq⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜y1y2⋮yi⋮yn⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟

即  Ax=b  
上述方程运用最小二乘法导出为线性平差计算的形式为： 
minx∥Ax−b∥2

最小二乘法的解

定理：线性方程组 Ax=b 的LS问题一定有解，且求解LS问题与求解线性方程组的法方程组等价 

ATAx=ATb

证明： 
rank(A)=rank(ATA)⇒rank(ATA)≤rank([ATA,ATb])=rank(aT[A,b])≤rank(AT)=rank(A)⇒rank(ATA)=rank([ATA,ATb])  
从而方程组一定有解 

f(x)=∥b−Ax∥2∥b−Ax∗∥2=minx∈Rn∥b−Ax∥2⎫⎭⎬⇒

gradf(x∗)=(∂f(x∗)∂x1,∂f(x∗)∂x2,…,∂f(x∗)∂xn)T=0⇒2(ATAx∗−ATb)=0

说明LS解必定是法方程组的解 

ATAx∗=ATb⇒AT(Ax∗−b)=0⇒Ax∗−b⊥R(A)={y∈Rm|y=Ax,x∈Rn}⇒∥b−Ax∥2=∥(b−Ax∗)+A(x∗−x)∥2=∥b−Ax∗∥2+∥A(x∗−x)∥2≥∥b−Ax∗∥2

说明法方程组的解必定是LS解

推论：当秩 (Am×n)=n 时， ATA 为对称正定矩阵，最小二乘法问题有唯一解 

xLS=(ATA)−1ATb

其中 (ATA)−1AT 称为A的伪逆矩阵，标记为 A†

证明： 
先将b拆成A的值域及其正交补两部分 
b=b1+b2  
b1=AA†b∈R(A)  
b2=(I−AA†)b∈R(A)⊥  
所以 Ax−b1∈R(A) ，可得 

∥Ax−b∥2=∥Ax−b1+(−b2)∥2=∥Ax−b1∥2+∥b2∥2

故当且仅当 x 是 Ax=b1=AA†b 解时， x 即为最小二乘解，即 x=A†b 。 
又因为 
N(A)=N(A†A)=R(I−A†A)={(I−A†A)h:h∈Cn}  
故 Ax=AA†b 的通解为 
x=A†b+(I−A†A)h:h∈Cn  
因为 

∥∥A†b∥∥2<∥∥A†b∥∥2+∥∥(I−A†A)h∥∥2=∥∥A†b+(I−A†A)h∥∥2,(I−A†A)h≠0

所以 A†b 又是二范数极小的最小二乘解。

例题：

求解超定方程组的最小二乘问题： 

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪2x1+4x2=13x1−5x2=3x1+2x2=62x1−x2=7⇒A=⎛⎝⎜⎜⎜23124−521⎞⎠⎟⎟⎟,b=⎛⎝⎜⎜⎜1367⎞⎠⎟⎟⎟

系数矩阵A是列满秩的，古可以求最小二乘法的解！ 

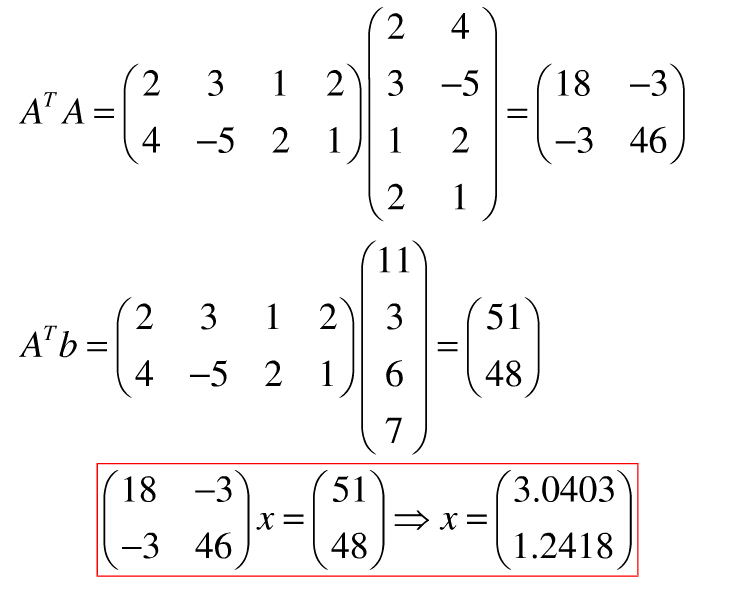
最小二乘法解为： 

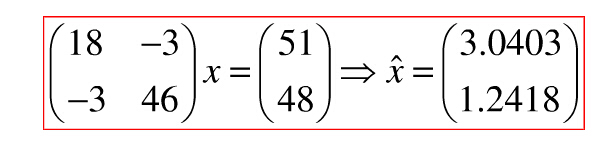
最小平方残差： 

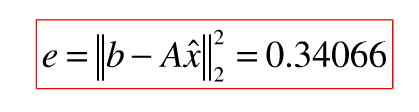
本例是用法方程组来求解最小二乘法问题的解！但是这样作也可能会引出好多问题！我们提倡用QR分解来求解。