1.线性回归介绍
X指训练数据的feature,beta指待估计得参数。
详细见http://zh.wikipedia.org/wiki/%E4%B8%80%E8%88%AC%E7%BA%BF%E6%80%A7%E6%A8%A1%E5%9E%8B
使用最小二乘法拟合的普通线性回归是数据建模的基本方法。
令最小二乘项的偏导为0(为0时RSS项最小),求Beta估计值,得到最小二乘的向量形式。
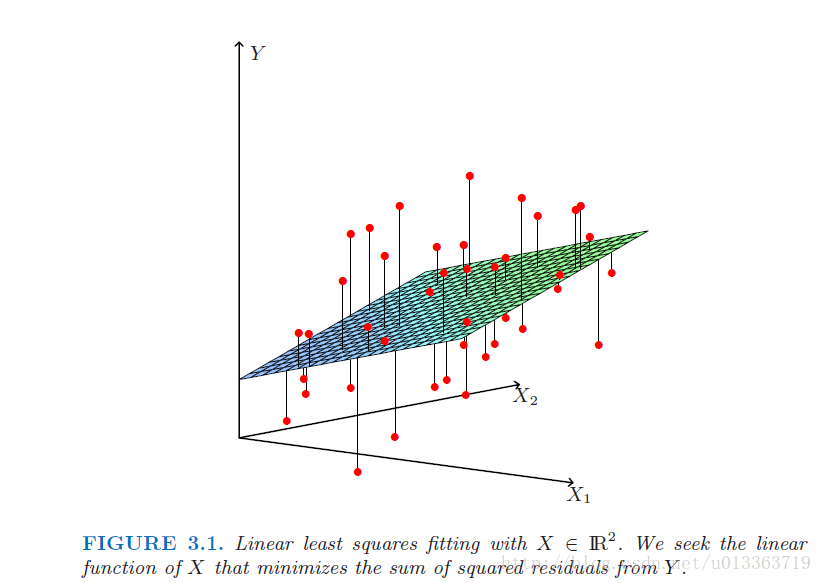
最小二乘其实就是找出一组参数beta使得训练数据到拟合出的数据的欧式距离最小。如下图所示,使所有红点(训练数据)到平面的距离之和最小。
图来源(ESL p45)








 线性回归是数据建模的基础,通过最小二乘法求解参数。然而,普通线性回归易发生过拟合。为解决此问题,引入正则化,包括岭回归(L2范数惩罚)和Lasso回归(L1范数惩罚)。岭回归使参数系数收缩,Lasso则可使部分系数为0,从而达到特征选择的效果。
线性回归是数据建模的基础,通过最小二乘法求解参数。然而,普通线性回归易发生过拟合。为解决此问题,引入正则化,包括岭回归(L2范数惩罚)和Lasso回归(L1范数惩罚)。岭回归使参数系数收缩,Lasso则可使部分系数为0,从而达到特征选择的效果。
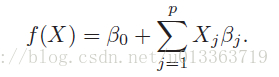
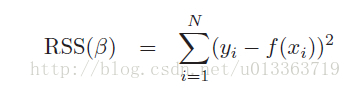
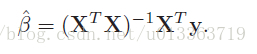
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1094
1094

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








