Mit6.006-problemSet03

3-1 哈希练习（Hash Practice）

(a)

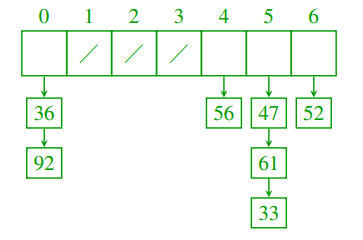
按顺序插入整数keys A=[47, 61, 36, 52, 56, 33, 92]到尺寸为7的哈希表中，使用哈希函数$h(k)=(10k+4)mod7$。哈希表的每个插槽，存储一个key（哈希到该插槽）的链表，后插入的追加到链表最后。所有key插入完成后，画一个哈希表的图。

(b)

假设哈希函数为：$h(k)=((10k+4)\mathrm{mod}c)\mathrm{mod}7$，c为某些整数。找到最小的c，从A中插入key时无碰撞发生。

解：根据pigeonhole原则，c<7时至少发生一个碰撞，因此串行地逐步增大c手动检测碰撞。如果c=7，那么47、61、33都哈希到5处。如果c=8，那么36、52、56、92都哈希到4。如果c=9，47、56都哈希到6。如果c=10，那么每个都哈希到4。如果c=11，那么47、36都哈希到1。如果c=12，那么56、92都哈希到0。如果c=13，没有碰撞。

A = [47, 61, 36, 52, 56, 33, 92]
for c in range(7, 100):
    hashes = [((10*k+4)%c)%7 for k in A]
    print('\t'.join([str(h) for h in hashes]))
    if len(set(hashes)) == 7:
        break

3-2 Dorm Hashing

MIT想分配2n个新学生到n个房间，编号0到n-1，在Pseudorandom Hall。每个MIT学生有一个ID：一个小于u的正整数，u>>2n。没有两个学生有相同的ID，但新学生被允许在学期开始后，选择他们自己的ID。

给定ID，MIT想很快的找到学生，因此将通过哈希他们的ID为一个房间号来分配学生到房间。为了不显得有偏见，在学期开始前（新学生选择他们ID前），MIT将在线发布一个哈希函数族H，学生选完ID后，MIT将随机地从H中选择一个统一的房间哈希函数。

新MIT学生Rony Stark和Tiri Williams想成为室友。

• Rony和Tiri可以选择ID k1和k2，保证他们成为室友

• 或证明这不可能，并计算他们可能成为室友的最大概率

(a)

H = { h a b ( k ) = ( a k + b ) m o d    n ∣ a , b ∈ { 0 , . . . , n − 1 } 且 a ≠ 0 } H=\{ h_{ab}(k)=(ak+b)\mod n|a,b\in\{0,...,n-1\}且a\neq0\} H={hab​(k)=(ak+b)modn∣a,b∈{0,...,n−1}且a=0}

解：Rony和Tiri可以选择任意两个ID k1、k2，让$k_1\equiv k_2\mathrm{mod}n$，这不难找到。比如Rony可以选择$k_1=3$，Tiri可以选择$k_2=2n+3$。对于所有a、b$a{k}_1+b\equiv a{k}_2+b\mathrm{mod}n$，因此Rony和Tiri被保证哈希到相同房间。

(b)

H = { h a ( k ) = ( ⌊ k n u ⌋ + a ) m o d    n ∣ a ∈ { 0 , . . . , n − 1 } } H=\{h_a(k)=(\lfloor\frac{kn}{u}\rfloor+a)\mod n|a\in\{0,...,n-1\}\} H={ha​(k)=(⌊ukn​⌋+a)modn∣a∈{0,...,n−1}}

解：因为$u>>n$，$\lfloor \frac{kn}{u}\rfloor$对于绝大多数相邻的值k是相同的，比如Rony可以选择$k_1=1$,Tiri可以选择$k_2=2$，结果都是0。添加常数a，采取结果mod n，a的值是否一样不会影响结果，因为$\lfloor \frac{kn}{u}\rfloor$总是一个0到n-1之间的整数，因此对于函数族中的任意函数，如果Rony和Tiri的ID有相同的哈希，他们将对函数族中所有函数拥有相同哈希。

(c)

H = { h a b ( k ) = ( ( a k + b ) m o d    p ) m o d    n ∣ a , b ∈ { 0 , . . . , p − 1 } 且 a ≠ 0 } H=\{ h_{ab}(k)=((ak+b)\mod p)\mod n|a,b\in\{0,...,p-1\}且a\neq0\} H={hab​(k)=((ak+b)modp)modn∣a,b∈{0,...,p−1}且a=0}

固定素数p>u（这是一个来自lecture4的统一哈希族）

解：对任意两个key，从统一哈希族中给定一个随机函数，它们碰撞的可能性至多为$\frac{1}{m}$，m为可能的哈希输出数量。因此，在这个情形中$\frac{1}{n}$是Rony和Tiri可以实现的最大的可能，不能保证它们是室友。

3-3 无论如何，寒冷并不可怕（The Cold is Not Bothersome Anyway）

冰芯是从深层冰川中钻出的长圆柱形塞子，这些塞子是堆积在一起并被压缩成冰的积雪。科学家可以将冰芯分成不同的切片，每个切片代表一年的沉积。对于下面每个场景，描述一个有效的算法来对从多个冰芯中收集的n个切片进行排序。验证你的答案。

(a)

每个冰芯给一个唯一的冰芯标识符用于记录，这是一个字符串（$16\lceil {\log }_4(\sqrt{n})\rceil$个ASCII字符）。通过冰芯标识符对切片排序。

解：每个字符串是一个连续$16\lceil {\log }_4(\sqrt{n})\rceil \times 8=\mathcal{O}(\log n)$的bit。在word-RAM中，这些bit可以被解释为存储在固定数量的机器字中的整数（$w\ge \lg n$），上边界是$2^{16\lceil {\log }_4(\sqrt{n})\rceil \times 8}<n^{33}$，因此我们可以通过基数排序对他们进行排序，耗时：$\Theta (n+n{\log }_n{n}^{33})=\Theta (n)$。

(b）

数据库中最深的冰芯高达800,000年。通过它们的年龄（切片形成后的年数）对切片进行排序。

解：年龄范围：$[0,8\ast 10^5]$，因此我们可以使用计数排序来对它们升序排列，最坏情形$\Theta (8\ast 10^5+n)=\Theta (n)$

(c)

每年降雪量的变化，会导致冰川在不同时间有不通的积累速度。对切片按厚度排序，$m/n^3$处于[0,4]，m是一个整数。

解：乘$n^3$，这些整数m的多项式边界：$[0,4n^3]$，因此对它们进行基数排序，最坏情形$\Theta (n+n{\log }_n{n}^3)=\Theta (n)$

(d)

Elna of Northendelle发现水有记忆，但不能量化给定切片的存储。幸运地是，给定2个切片，她可以区分哪个有更多的存储（花费$\mathcal{O}(1)$，使用她的“双指算法”，用她的两个手指触碰切片）。通过存储对切片排序。

解：在切片中，仅有的辨别顺序信息的方式是通过比较，因此我们可以选择归并排序，耗时$\Theta (n\log n)$，在比较模型中，这是最优的。

3-4 pushing paper

Farryl Dilbin是一个Munder Difflin造纸公司中央仓库的叉车操作人员。她需要运送r reams的纸给客户。在仓库中有n箱纸，每箱1英尺宽，并排排列，覆盖着一堵n英尺的墙。每个箱子包含一个已知的正整数ream，没有两个箱子包含相同数量的ream。让$B=(b_0,...b_{n-1})$代表每个箱子中有多少ream，箱子i位于从左到右第i英尺处，包含$b_i$ reams的纸，对于所有$i\ne j，b_i\ne b_j$。为了最小化她的工作，Pharryl想知道是否有一对相近的箱子$(b_i,b_j)$，意味着$|i-j|<n/10$，满足订单r，意味着：$b_i+b_j=r$。

(a)

给定B和r，描述一个期望$\mathcal{O}(n)$时间的算法，来决定是否B包含一对相近箱子满足订单r。

解：对每个$b_i$满足$r-b_i=b_j,b_j\in B$，若满足，则检查$|i-j|<n/10$。因为每个箱子有唯一数量的ream，如果$b_i$有匹配的，那么有唯一的$b_j$。原生地，我们可以执行这个检查，通过比较$r-b_i$和所有 b j ∈ B − { b i } b_j\in B-\{b_i\} bj​∈B−{bi​}，每个$b_i$耗时$\mathcal{O}(n)$，导致$\mathcal{O}(n^2)$。我们可以对这个算法加速，通过首先将B中所有元素放到哈希表H，比如$(b_i,i)$，因此查询每个$r-b_i$可以很快完成。对每个$b_i\in B$，插入$b_i$到H，映射i，花费期望摊还$\mathcal{O}(1)$时间。现在B中所有值都存在于H中，因此对每个$b_i$，检查$r-b_i$是否存在于H中，花费期望$\mathcal{O}(1)$。那么，如果这么做了，H将返回j，用于测试与i的相邻程度，花费$\mathcal{O}(1)$。构建哈希表，检查每个匹配花费期望$\mathcal{O}(n)$，因此这个算法执行时间：期望$\mathcal{O}(n)$。这个暴力算法是正确的，我们检查每个$b_i$和它仅有可能满足的伙伴，检查它是否离得够近。

(b)

现在假设$r<n^2$。描述一个最坏情形$\mathcal{O}(n)$时间复杂度的算法，来决定B是否包含一组相邻对，满足订单r。

解：用元组$(b_i,i)$取代B中的$b_i$，来记录箱子原始顺序的索引。我们不知道$b_i$在n的多项式内；但我们知道r是。如果$b_i\ge r$，那么它不是B中满足订单r的元组的一部分。因此执行B的线性扫描，移除所有$(b_i,i)b_i\ge r$，构建集合$B^{\prime }$。现在$B^{\prime }$中ream的个数$b_i$，上边界都是$\mathcal{O}(n^2)$，因此我们可以通过他们的ream数$b_i$对$B^{\prime }$中的元组排序，使用基数排序最坏情形$\mathcal{O}(n+n{\log }_n{n}^2)$，并将输出存到数组A中。

现在我们可以使用双指算法（与归并排序中的归并步骤相似）扫过有序链表来找到相加为r的元组（如果这个元组存在）。特别地，初始化索引$i=0，j=|A|-1$，重复下面过程，直到i=j。如果$A[i]=(b_k,k)，A[i].b=b_k，A[i].x=k$。有3种情形：

• A[i].b+A[j].b=r：满足订单的元组已经找到，检查$|A[i].x-A[j].x|<n/10$，返回true或false

• $A[i].b+A[j].b<r$：$A[i].b$不会是满足订单的元组（对于 A [ k ] . b ， k ∈ { i + 1 , . . . , j } A[k].b，k\in \{i+1,...,j\} A[k].b，k∈{i+1,...,j}），因此提升i

• $A[i].b+A[j].b>r$：$A[j].b$不会是满足订单的元组（对于 A [ k ] . b ， k ∈ { i , . . . , j − 1 } A[k].b，k\in\{i,...,j-1\} A[k].b，k∈{i,...,j−1}），因此降低j

循环每次开始时，维持不变性：我们确认没有元组$(A[k].b,A[l].b)$是够近的，是满足订单的，$k\le i\le j\le l$，因此我们到达最后，不会返回有效的元组，算法将正确地推断没有这样的元组。因为每次循环的迭代花费$\mathcal{O}(1)$，并且$j-i$减少1，$j-i=|B^{\prime }|-1$起始于整数，结束于$j-i<0$，这个过程最坏情形花费$\mathcal{O}(n)$

3-5 Anagram Archaeology

如果A是B中字母全排列，字符串A是另一个字符串B的anagram；举例：(indicatory，dictionary)和(brush，shrub)是互为anagram的单词对。在这个问题中，所有字符串是ASCII字符串，仅包含小写英文字母a到z。

给定两个字符串A和B，B在A中的anagram substring count，是A中连续子字符串为B的anagram的数量。举例，如果A=‘esleastealaslatet’，B=‘tesla’，A中有13个长度为|B|=5的连续字符串，它们中的3个是B的anagram，名为(‘least’,‘steal’,‘slate’)，因此B在A中的anagram substring count是3。

(a)

给定字符串A和正整数k，描述一个数据结构，可以花费$\mathcal{O}(|A|)$时间构造，支持单个操作：给定一个不同的字符串B，|B|=k，返回B在A中的anagram substring count，花费$\mathcal{O}(k)$。

解：对于这个数据结构，我们需要一个方式，找到A中多少子字符串是输入B的anagram，运行时间不依赖|A|。这个方法将会构建、存储每个字符串固定大小的cannonicalization到哈希表中，字符串的多个anagram有相同的cannonicalization。特别地，我们将构建一个26个entry的频率表，每个对应一个英文字母，每个entry存储该字符串中字母出现的次数。当且仅当它们互为anagram时，两个字符串有相同的频率表。

让$S=(S_0,...,S_{|A|-k})$是$|A|-k+1$个连续的长度为k的A子字符串，子字符串$S_i$起始于字符$A[i]$。对每个$S_i\in S$原始地构建频率表，花费$\mathcal{O}(|A|k)$。然而，原始地花费$\mathcal{O}(k)$计算$S_0$的频率表，我们可以通过$S_i$的频率表为$S_{i+1}$构建频率表，减掉$S_i$处频率表的在$A[i]$处的字母，加上$A[i+k]$处的字母。以这种方式，对于每个$S_i\in S$，我们可以计算固定长度的频率表，花费$\mathcal{O}(k)+(|A|-k)\mathcal{O}(1)=\mathcal{O}(|A|)$。将每个频率表插入到哈希表H，映射着频率表拥有的数量，花费$\mathcal{O}(|A|)$。每个频率表至多为n，因此每个频率表可以被视作一个$26\lceil \lg n\rceil$长度的整数，占用固定数量的机器字，可以被当作一个哈希key。

给定我们的数据结构H，为了支持请求操作，我们可以通过首先计算输入字符串B的频率表f（花费$\mathcal{O}(k)$），然后花费期望$\mathcal{O}(1)$在H中寻找它，总共期望$\mathcal{O}(k)$。因为$H(f)$存储了频率表f和$S_i\in S$的数量，如果f在H中，存储的值会是B在A中的anagram substring count。否则，如果f不再H中，f不是A的任意子字符串的anagram，因此返回0。

(b)

给定字符串T和一个拥有n个长度为k字符串（$S=(S_0,...,S_{n-1})$）的数组，满足$0<k<T$，描述一个$\mathcal{O}(|T|+nk)$时间复杂度的算法，返回一个数组$A=(a_0,...,a_{n-1})$，$a_i$是$S_i$在T中的anagram substring count（ i ∈ { 0 , . . . , n − 1 } i\in\{0,...,n-1\} i∈{0,...,n−1}）。

解：构建(a)中的数据结构，用T取代A，使用k，花费期望$\mathcal{O}(|T|)$。那么对于每个$S_i\in S$，我们可以通过数据结构执行操作，花费$\mathcal{O}(k)$，存储它们的输出到一个数组A中，总计期望$\mathcal{O}(|T|+nk)$。这个算法的正确性，基于(a)中数据结构的正确性。

(c)

写一个python函数count_anagram_substrings(T, S)，实现part(b)中的算法。注意内置python函数ord©，返回对应ASCII字符c的ASCII整数，花费$\mathcal{O}(1)$。你可以从网站下载一些包含测试用例的代码模板。

解：

ORD_A = ord('a')
def lower_ord(c):
    return ord(c) - ORD_A

def count_anagram_substrings(T, S):
    m, n, k = len(T), len(S), len(S[10])
    D = {}
    F = [0] * 26
    for i in range(m):
        F[lower_ord(T[i])] += 1
        if i > k - 1:
            F[lower_ord(T[i - k])] -= 1
        if i >= k - 1
            key = tuple(F)
            if key in D:
                D[key] += 1
            else:
                D[key] = 1
    A = [0] * n
    for i in range(n):
        F = [0] * 26
        for c in S[i]:
            F[lowser_ord(c)] += 1
        key = tuple(F)
        if key in D:
            A[i] = D[key]
    return tuple(A)