牛顿迭代法 | 溯源 / 原理 / 应用

注：本文为“牛顿迭代法”相关文章合辑。

图片清晰度受引文原图所限。
略作重排，未整理去重。
如有内容异常，请看原文。

---

“数” 往开来 | 牛顿迭代法

数学中国 2024 年 07 月 28 日 17:29 内蒙古

牛顿迭代法，探秘方程的近似求解之旅

如何求解方程 $x-cos(x)=0$ 的根？如何求解方程 $x^3+2x^2+3x+4=0$ 的根？这些方程形式看似简单，却很难求出其精确的根。事实上，数学史上有一个著名的阿贝尔 - 鲁菲尼定理，它指出五次及更高次的代数方程没有一般的代数解法，即这样的方程是不能由方程的系数经有限次四则运算和开方运算求出精确根的。但这并不意味着方程无解，我们需要的是所谓 “数值方法” 一步一步逼近解，算到精度够了就行。

在数学的广袤天地里，非线性方程如同一座座等待攀登的高峰，它们复杂多变，却又蕴含着自然界的深刻规律。这类方程广泛存在于物理学、工程学、经济学等众多领域，是描述复杂系统行为的重要工具。例如，在物理学中，我们可以利用这些方法求解天体运动的轨迹、材料的非线性力学响应等问题；在工程学中，它们被用于结构分析、流体力学模拟等领域；在经济学中，非线性方程计算方法则帮助我们理解市场均衡、经济增长等复杂经济现象。

求解非线性方程常用的数值方法包括二分法、牛顿法、割线法、单纯形算法、同伦延招法、区间迭代法等等，本文将介绍其中经典且高效的牛顿迭代法。

01｜什么是牛顿迭代法？

牛顿迭代法（Newton’s method），又称为牛顿 - 拉夫逊方法（Newton-Raphson method），是数学星空中一颗璀璨的明星。它源自 17 世纪伟大的科学家艾萨克・牛顿，又由拉夫逊、辛普森、傅里叶等数学家完善。牛顿迭代法基本思想是利函数在某点的切线来估计方程的根，通过不断迭代，逐步逼近真实解。

02｜原理揭秘

设待求解的方程为 f (x)=0。一个根的初始猜测值记为 X0, 那么在 X0 点的切线可以表示为

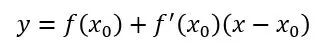
公式 1

这条切线与 x 轴的交点记为 X1，则

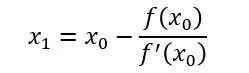
公式 2

再过 X1 做切线，同理得到 X2,X3…

递推表达式为

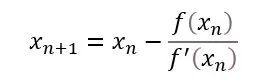
公式 3

由此不断更新的 Xn 会趋于精确解。

03｜应用实例

下面的视频我们会给出牛顿迭代法的具体算法和针对实际问题的 C 语言代码流程，主要的思想是将存储解的 x0 不断更新，并比较新解和旧解的差距来判断是否收敛到所需精度范围内。此外，从之前的原理介绍中我们可知牛顿法的适用范围要求代解方程可求导。

04｜结语

牛顿迭代法，这一源自 17 世纪的古老算法，至今仍以其简便性和高效性在数学和工程领域发挥着重要作用。更深入的研究还包括牛顿迭代法收敛阶衡量，下山法、割线法改进方法，求解方程组的迭代法等等。随着计算机技术的飞速发展，数值解法的效率和精度不断提高，为我们揭示了更多自然界的奥秘。未来，随着算法的不断创新和优化，我们有理由相信，非线性方程计算方法的领域将会迎来更加辉煌的明天。

编辑 / 张志红

审核 / 范瑞强

复核 / 张志红

---

一口气看完牛顿迭代法（课本中的高数背景）

原创 加林查 旭哥玩数学 2024 年 10 月 12 日 22:13 浙江

高中数学课本任教版选择性必修二中介绍了一种解方程的数值方法 —— 牛顿迭代法。

下面我们来回答课本中最后留下来的两个思考题：

1. 不同的初始值对求方程的近似解有影响吗？如果有，影响在什么地方？

2. 你还知道其他求解方程近似解的方法吗？你认为牛顿法的优点和缺点是什么？

---

牛顿迭代法的可视化详解

数据派 THU 2022 年 02 月 22 日 17:05 北京

来源：DeepHub IMBA

本文利用可视化方法，为你直观地解析牛顿迭代法。

牛顿迭代法（Newton’s method）又称为牛顿 - 拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在 17 世纪提出的一种在实数域和复数域上近似求解方程的方法。

以 Isaac Newton 和 Joseph Raphson 命名的 Newton-Raphson 方法在设计上是一种求根算法，这意味着它的目标是找到函数 f (x)=0 的值 x。在几何上可以将其视为 x 的值，这时函数与 x 轴相交。

Newton-Raphson 算法也可以用于一些简单的事情，例如在给定之前的连续评估成绩的情况下，找出预测需要在期末考试中获得 A 的分数。其实如果你曾经在 Microsoft Excel 中使用过求解器函数，那么就使用过像 Newton-Raphson 这样的求根算法。另外一个复杂用例是使用 Black-Scholes 公式反向求解金融期权合约的隐含波动率。

Newton-Raphson 公式

虽然公式本身非常简单，但如果想知道它实际上在做什么就需要仔细查看。

首先，让我们回顾一下整体方法：

1. 初步猜测根可能在哪里？

2. 应用 Newton-Raphson 公式获得更新后的猜测，该猜测将比初始猜测更接近根。

3. 重复步骤 2，直到新的猜测足够接近真实值。

这样就足够了吗？Newton-Raphson 方法给出了根的近似值，尽管通常它对于任何合理的应用都足够接近！但是我们如何定义足够接近？什么时候停止迭代？

一般情况下 Newton-Raphson 方法有两种处理何时停止的方法。1、如果猜测从一个步骤到下一步的变化不超过阈值，例如 0.00001，那么算法将停止并确认最新的猜测足够接近。2、如果我们达到一定数量的猜测但仍未达到阈值，那么我们就放弃继续猜测。

从公式中我们可以看到，每一个新的猜测都是我们之前的猜测被某个神秘的数量调整了。如果我们通过一个例子来可视化这个过程，它很快就会清楚发生了什么！

作为一个例子，让我们考虑上面的函数，并做一个 x=10 的初始猜测（注意这里实际的根在 x=4）。Newton-Raphson 算法的前几个猜测在下面的 GIF 中可视化👇

我们最初的猜测是 x=10。为了计算我们的下一个猜测，我们需要评估函数本身及其在 x=10 处的导数。在 10 处求值的函数的导数只是简单地给出了该点切线曲线的斜率。该切线在 GIF 中绘制为 Tangent 0。

看下一个猜测相对于前一个切线出现的位置，你注意到什么了吗？下一个猜测出现在前一个切线与 x 轴相交的位置。这就是 Newton-Raphson 方法的亮点！

事实上， f (x)/f’(x) 只是给出了我们当前猜测与切线穿过 x 轴的点之间的距离（在 x 方向上）。正是这个距离告诉我们每次更新的猜测是多少，正如我们在 GIF 中看到的那样，随着我们接近根本身，更新变得越来越小。

如果函数无法手动微分怎么办？

上面的例子中是一个很容易用手微分的函数，这意味着我们可以毫无困难地计算 f’(x)。然而，实际情况可能并非如此，并且有一些有用的技巧可以在不需要知道其解析解的情况下逼近导数。

这些导数逼近方法超出了本文的范围，可以查找有关有限差分方法的更多信息。

问题

敏锐的读者可能已经从上面的示例中发现了一个问题，示例函数有两个根（x=-2 和 x=4），Newton-Raphson 方法也只能识别一个根。牛顿迭代会根据初值的选择向某个值收敛，所以只能求出一个值来。如果需要别的值，是要把当前求的根带入后将方程降次，然后求第二个根。这当然是一个问题，并不是这种方法的唯一缺点：

• 牛顿法是一种迭代算法，每一步都需要求解目标函数的 Hessian 矩阵的逆矩阵，计算比较复杂。

• 牛顿法收敛速度为二阶，对于正定二次函数一步迭代即达最优解。

• 牛顿法是局部收敛的，当初始点选择不当时，往往导致不收敛；

• 二阶 Hessian 矩阵必须可逆，否则算法进行困难。

与梯度下降法的对比

梯度下降法和牛顿法都是迭代求解，不过梯度下降法是梯度求解，而牛顿法 / 拟牛顿法是用二阶的 Hessian 矩阵的逆矩阵或伪逆矩阵求解。从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想）。

那为什么不用牛顿法替代梯度下降呢？

• 牛顿法使用的是目标函数的二阶导数，在高维情况下这个矩阵非常大，计算和存储都是问题。

• 在小批量的情况下，牛顿法对于二阶导数的估计噪声太大。

• 目标函数非凸的时候，牛顿法容易受到鞍点或者最大值点的吸引。

实际上目前深度神经网络算法的收敛性本身就是没有很好的理论保证的，用深度神经网络只是因为它在实际应用上有较好的效果，但在深度神经网络上用梯度下降法是不是能收敛，收敛到的是不是全局最优点目前还都是无法确认的。并且二阶方法可以获得更高精度的解，但是对于神经网络这种参数精度要求不高的情况下反而成了问题，深层模型下如果参数精度太高，模型的泛化性就会降低，反而会提高模型过拟合的风险。

作者：Rian Dolphin

---

牛顿迭代法传奇（上）：张冠李戴的命名

原创 曾钟钢、丁玖 返朴 2021 年 06 月 26 日 08:11

作为解方程的基本通用算法，牛顿法是应用数学和计算数学最重要的算法之一。这个简单神速的算法被冠以牛顿大名，那它真是牛顿发现的吗？

撰文 | 曾钟钢（美国东北伊利诺伊大学数学系讲座教授）、丁玖（美国南密西西比大学数学系教授）

传说三千五百年前，聪明的巴比伦人想出了一个计算平方根简单漂亮的窍门：如果一个正数比 $\sqrt{\text{A}}$ 小一点，则 A 除以它就比 $\sqrt{\text{A}}$ 大一点，这样它们的平均值就有希望更靠近 $\sqrt{\text{A}}$ 。于是，先取 $\sqrt{\text{A}}$ 的一个大致估计记为 a， 只需求 a 和 $\frac{\text{A}}{\text{a}}$ 的平均，写成公式就是

算出的 b 就是 $\sqrt{\text{A}}$ 更精确的近似值 。

神奇的是，如果你的初始估计不是太差，比如猜到 $\sqrt{2}\approx 1.4$ 作为 a 有两位数字精确，那么 $b\approx 1.414$ 就有四位数字精确。用同样办法改进 b 得到 $c\approx 1.4142136$ 的精确数字就有八位。每次计算精确数位翻一番！

猜不出初始近似怎么办呢？没关系，从任何非零正数 a 出发都可以。随意乱猜的结果无非是多算几步，很快就会进入精度加倍状态。这个方法流传至今成为经典传奇，叫做巴比伦方法。为什么说是个传奇？因为没有文字记载。直到公元 60 年，古希腊数学家 Hero of Alexandria (c. 10-c.70) 对这个方法才给出了有案可查的第一个明确的表述，所以巴比伦法也称为赫伦方法 （Heron’s method）。现在我们知道， 本文主题牛顿迭代法最古老的源头来自四大文明之一的巴比伦文明。

什么是牛顿迭代法？

牛顿 (Isaac Newton，1643-1727) 的大名就无需介绍了。他以发现力学三大定律、万有引力定律和微积分跻身从古到今最伟大的科学家行列。牛顿无疑是有史以来最杰出的数学家之一。作为一个重大贡献，他率先发现的微积分可以上升到人类文明瑰宝的高度。所有的理工科大学生都应该知道赫赫有名的 “牛顿法”，也称 “牛顿迭代” 或 “牛顿近似”。自然科学家、应用和计算数学家及工程学家们一旦需要求解非线性方程和方程组，脑子里首先应该想到的就会是牛顿法。

什么是牛顿法呢？设想我们要求出一元非线性方程 f (x) = 0 的解，比如说 $x–cosx=0$，这里 $f(x)=x–cosx$ 。数学史上有个著名的阿贝尔不可能定理，说的是非线性方程一般来说是不可能保证找到精确解的，门都没有。所以我们需要所谓 “数值方法” 一步一步地逼近解，算到精度够了就行。假如 f (x) 有导函数 f’(x) ，牛顿法就是这样的迭代程式：先取一个初始点 x0 作为解的近似，然后按下面的简单公式依次迭代：

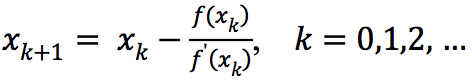(1)

就得到一个序列 $x0,x1,x2,\dots$ 。只要满足三个并不苛刻的条件：（i）函数 $f(x)$ 二次连续可导，（ii）在所求解 $x\ast$ 处导数非零，加上（iii）初始近似 $x0$ 足够接近 x*，则这个序列将快速趋近 ，基本上是每一步精确数位加倍。因此，实际计算中大多三五步迭代就可以获得足够精确的近似解。读者可以很容易验证，巴比伦方法其实就是求解平方根方程 x2-A=0 的牛顿迭代。当然啦，巴比伦人不大可能知道 “迭代” 这个概念。

你要作科学计算和工程计算吗？几乎所有问题要么本身就是个方程，要么一定会在某个步骤需要解方程。作为解方程的基本通用算法，牛顿法是应用数学和计算数学最重要的算法之一。这个简单神速的算法被冠以牛顿大名，那它真是牛顿发现的吗？这是个历史悠久又颇有争议的传奇故事，其间包含数学史上一个个如雷贯耳的名字。

经久不衰的 “谬误”

现在大家用的代数符号和表达式体系，创始人是法国人韦达 (François Viète，1541-1603) 。他的谋生职业是律师，他还做过亨利三世和四世的王室智囊，挣足了钱给自己提供经费研究数学并将结果出版。除了代数上的造诣，他还是方程理论的大师。他计算能力超强，在欧洲首次算出十位精确圆周率值。韦达在十七世纪初提出了一个多项式方程求根的算法，每一次计算精度数位增加一位。用现在的话说叫线性收敛或一阶收敛。韦达的算法解释起来很费功夫，有兴趣的读者可以参考引文 [1] 。

据文献 [2] 考证，牛顿于 1664 年左右读到韦达的技巧，约 1669 年写入《分析论》（De analysi）。但这部书直至 1711 年才由威尔士数学家琼斯（William Jones，1675-1749）为他编辑出版。牛顿在书中改进了韦达的思路，提出一个近似求解多项式方程的新方法。以三次方程 $x^3–2x–5=0$ 为例。他首先注意到在 2 与 3 之间有个解（读者可以用介值定理验证），于是他把这个解写成 $x=2+p$ ， 代入原方程化简后得到 p 的三次方程 $p3+6P^2+10p–1=0$。当然，解这个新方程看起来跟老方程一样困难。但 p 的方程可以用上微积分的思路求解：因为 p 很小，它的平方和立方就更小，于是三次函数 $p^3+6p^2+10p–1$ 可以用线性部分 $10p–1$ 近似。解 $10p-1=0$ 得到 $p\approx 0.1$ 。也就是 x 的近似从 2 到 2.1， 精确数位翻倍。

然后，牛顿依法炮制，即令 $p=0.1+q$，代入 $0=p^3+6p^2+10p–1$：

$0=(0.1+q{)}^3+6(0.1+q{)}^2+10(0.1+q)-1=q^3+6.3q^2+11.23q+0.061\approx 11.23q+0.061$

得到 q ≈ -0.0054，也就是 $x=2.1+q\approx 2.0956$ 。再令 $q=-0.0054+r$，同法得 $r\approx -0.00004852$ 。这样经过三步以后，牛顿找到原方程的一个 8 位精确的近似解：

$x=2+p+q+r\approx 2+0.1-0.0054-0.00004852=2.09455147$

每算一步精确数位加倍！

在其 1687 年首版的辉煌巨著《自然哲学的数学原理》中，牛顿求解了用于天文学的 x – e sin x = M 这个超越方程。他将其中的正弦函数用级数展开，得到一个近似的多项式方程。然后他就可以用上述数值逼近多项式方程解的法子得到原方程的近似解。正如他在二十年前所做的那样，他没有明确地用到函数的导数概念来推导这个数值方法，也没有明确提出迭代概念和公式。

这就是后人所知牛顿参与创立 “牛顿法” 的过程。牛顿的贡献是用微积分思路，在韦达方法的基础上把巴比伦方法从平方根方程 x2-A=0 推广到一般的多项式求根。

英国科学史专家 Nicholas Kollerstrom 于 1992 年发表了一篇关于牛顿法的考证文章 [3] 。文章的标题很有意思：《托马斯・辛普森和 “牛顿近似法”：一个经久不衰的迷思》。意思是说把公式（1）称为 “牛顿法” 是个迷思（myth），也就是一个广泛流传的谬误，而且这个谬误 “经久不衰”。他指出，牛顿法（1）有两个重要的特征：1. 它是一个迭代过程；2. 它采用了微分表达式。而这两个特征中的哪一个，都没有在牛顿的《分析论》里出现。迭代法在理论上是一个无穷极限过程，牛顿只给出了三步计算演示。其实还可以加上一条：由于没有使用微分，牛顿提出的方法只能用于多项式，不是一个通用算法。

第一个真正的迭代法

数值计算求解方程的第一个真正意义上的迭代法是跟牛顿同在英国的约瑟夫・拉夫森（Joseph Raphson，1648-1715）在他于 1690 年发表的文章《方程分析通论》中给出的近似方法。但它同样没有求导运算，因此不符合 “牛顿法” 的第二个特征。然而，一些慷慨的后人，包括部分现代数学家，把 “牛顿法” 的勋章切成一半分给了拉夫森 —— 称之为 “牛顿 - 拉夫森法”。

那么，拉夫森是怎么获得他的数值方法的呢？我们用求解三次方程 x^3 – ax + b = 0 来描述他的求解方案。在每次迭代中，他分两步走。设目前的近似解为 u，则将下一个的近似解写成 u + d。然后用 x=u + d 代入方程并按二项式公式展开，这是第一步。在第二步，合并同类项得到 d 的一次项的系数 3u2 – a，然后令 ，这样得到下一个近似解。

拉夫森强调用他的上述办法周而复始地迭代下去，就可以计算出满足任意精确的方程解。然而我们依然看不到求导数运算的影子。此外，他仅仅对多项式方程提出了这个迭代法，用到的二项式公式无法直接推广到像求解超越方程这样的情形。在他最初由伦敦皇家学会发表的那篇文章的前言里，他提到他的方法与牛顿之前的做法有类似之处。然而，七年后的 1697 年，当他把这个方法著书时没提牛顿的名字，而说韦达是他的方法的始祖。

如果我们比较牛顿和拉夫森的做法，不难发现，牛顿用到一个经过代入步骤而导出的一个似乎更加复杂的多项式，再丢掉高阶项求得近似；拉夫森从头到尾都是用给定的原多项式，运算要简单得多。拉夫森感觉自己的方法跟牛顿是完全不一样的推导，无需归功于牛顿。类似的比较也陆续出现。比如，在 1796 年发表的文章《关于拉夫森先生的方法的观察》中，作者费伦德（W. Frend）比较了两法的各自优点：“考虑到两种方法的简单性和概念性… 我认为总的来说，拉夫森先生求解方程的方法比艾萨克・牛顿爵士的更为方便。”

在 1798 年，法国大数学家拉格朗日 (Joseph-Louis Lagrange，1736-1813) 发表了颇具影响力的论文《数值求解方程》。他精细化并推广了牛顿著作《分析论》中的方法，但依然没有用到导数或微分术语。

眼尖的读者很快就发现，在上述拉夫森得到的 d 的分数表达式中，分子就是函数 x3 – ax + b 在当前迭代点 u 的值，而分母恰恰就是这个函数的导数在此迭代点的负值，因而这就给出了 “牛顿法” 在多项式函数的全部内容。然而，不能因此就说拉夫森发明了今日所称的牛顿法！原因就在于他和牛顿一样，都没有使用导数的记号和运算而得出一般的牛顿法格式，仍然无法直接应用到一般的非线性方程。

被忘却的发明人

那么，谁才是 “牛顿法” 当之无愧的发明人呢？

此人的全名是托马斯・辛普森（Thomas Simpson，1710-1761），他是比牛顿和拉夫森迟了几十年的英国数学家。他就是近似数值积分著名的 “辛普森法则” 的那个辛普森。有意思的是，辛普森在牛顿法贡献恐怕最大，却被后人差不多忘得一干二净。他反而在数值积分法获得并非实至名归的荣誉。该得的没得到，不该得的反而拿着了。早他一百年，德国天文学家开普勒（Johannes Kepler，1571-1630）就已经发现了近似计算 “曲边矩形” 面积的该项法则。因此，德国人把我们叫惯了的辛普森法则自豪地称作为 “开普勒的桶法则”，就像我们常常把关于二项展开式各项系数的 “帕斯卡三角形” 称为 “杨辉三角形” 那样异曲同工。

辛普森构造出现代意义下的牛顿法是在 1740 年，此时牛顿已经去世了十三年。那年他出了一本关于数学的论文集，其中一篇描述了 “求解方程的一个新方法”，却没有列出任何先驱者的姓名。在前言部分，他断言：“因为它比以往的任何方法都更普遍，它不能不具有相当大的用途。” 这听上去口气很大。他是自信而非吹牛：“取给定方程的流数……” 此处，流数的英文是 fluxion，正是牛顿当年用来表示今天我们所称的 “导数” 的那个东西 —— 函数的瞬时变化率。接着，他给出了和上面公式 (1) 式实际一模一样的迭代程序，除了没有采用当今标准的、微积分另一发明人莱布尼茨（Gottfried Leibniz，1646-1716）所引进的导数记号。

辛普森用这个普遍方法做了五个例子，包括求解三次方程、平方根计算、指数方程等。更进一步，他第一个将他的方法用于求解含有两个未知数和两个方程的方程组！既然他是有史以来第一个完整地提出和今日所指的牛顿法有完全相同格式的迭代法，数学史专家 Kollerstrom 得出结论：辛普森才是牛顿法的发现者。

辛普森版的牛顿法跟现代教科书的差别仅仅是所用的符号。他应当之无愧地被授予创造该法的荣誉。然而，到底是谁写出了现代形式的牛顿法呢？

他就是在近代数学向前迈步的崎岖道路上留下巨大脚印的傅里叶（Joseph Fourier，1768-1830）。这位法国数学家在辛普森提出标准的牛顿法后的第二十八个年头才出生。在十九世纪初，他首次用当今世界通用的导数记号 f’重新叙述了迭代法 (1)，同时把它说成是 “牛顿法”。由于拉格朗日的那篇雄文，后来，有些英国数学家将此法称为 “牛顿和拉格朗日的方法”，而对拉夫森只字不提。十九世纪的数学史名家、德国人康托尔（Moritz Cantor，1829-1920）考察了牛顿、拉夫森等人的方程近似求解法，把拉夫森描绘为 “牛顿的绝对仰慕者和模仿者”，认为他的近似法 “与牛顿的方法极其类似”。

瑞士出生的美国数学史家弗洛里安・卡乔里（Florian Cajori，1859-1930）在 1911 年的《美国数学月刊》上发文提出这个方法理应被称为 “牛顿 - 拉夫森法”。但是，他的命名论据受到 Kollerstrom 的质疑，依据正是那个 “两个特征”，后者认为荣誉只能归于辛普森。然而，著名的数学史家博耶（Carl Boyer，1906-1976）在他 1968 年出版的大作《数学史》中这样断言：“方程近似求解的牛顿法可在《分析论》中发现。” 由于牛顿在科学史包括数学史上的巨大名望，拥有 “牛顿法” 的真正主人辛普森在数学史上几乎失去了立足之地，拉夫森也只能偶然出现在牛顿名字的后面。

这种张冠李戴的命名在科学和数学史中比比皆是。例如，学过初等微积分的人都知道求不定式极限的 “洛必达法则”，实际上是瑞士数学家伯努利（Johann Bernoulli，1667-1748) 的杰作。伯努利的数学功力可不是法国数学家洛必达 (Guillaume de l’Hôpital，1661-1704) 所能望其项背的。洛必达于 1694 年 3 月 17 日在给伯努利的信中，提出每年给他三百法郎换取他的最新数学发现，并且不能透露给第三者。当年伯努利告诉了洛必达这个求极限定理，两年后洛必达将它写进了自己的著作《曲线的无穷小分析》，据说这是全世界的第一本微积分教材。尽管洛必达在书中感谢了莱布尼茨和伯努利，尤其感谢伯努利，或许作者有意无意地没有明确承认 “洛必达法则” 是诞生于别人家的婴儿，不明就里的后人就把这条极其有用的求极限法则冠上了他的名字。当然伯努利在数学史上大名鼎鼎，少了个洛必达法则也不至于沦落成籍籍无名的历史过客。

牛顿法的基本思想和深层含义是什么？哪些激情探索者又续写传奇？且待下篇

后记：作者以此文纪念我们的导师李天岩教授（1945 年 6 月 28 日 - 2020 年 6 月 25 日）逝世一周年。

参考文献

[1] Tjalling J. Ypma, Historical Development of the Newton-Raphson Method, SIAM Review, 37, 531-551, 1995

[2] P. Deuflhard，“A short history of Newton’s method，”Documenta Math.，Extra Volume ISMP，25，25-30，2012.

[3] N. Kollerstrom，“Thomas Simpson and ‘Newton’s method of approximation’：an enduring myth，”BJHS，25, 347-354，1992.

---

牛顿迭代法传奇（下）：意犹未尽，柳暗花明

原创 曾钟钢、丁玖 返朴 2021 年 06 月 29 日 07:52

一项科学发现常常只能被幸运地发现一次。而牛顿法则一次次被重新推广和修正，每次新发现的结果是，我们原来知道的牛顿法不过是新版的特例而已。其发展和演变历史，正是数学学人不断探索新领域解决新问题过程的写照。牛顿法的奇妙还在于，从诞生以来的一次次发展、推广和创新都是实质性的，而不仅仅是修边角式的改善。

撰文 | 曾钟钢（美国东北伊利诺伊大学数学系讲座教授）、丁玖（美国南密西西比大学数学系教授）

在《牛顿迭代法传奇（上）：张冠李戴的命名 》中我们说到，科学计算和工程计算上最基本最重要的通用算法 “牛顿法” 的发明史，是一部诸多大数学家前仆后继的传奇史，从巴比伦 - 赫伦，到韦达，到牛顿，到拉夫森，到辛普森等等，许多数学家将看似简单的牛顿法不断赋予新的内涵。直至今天，这个传奇仍旧没有结束，本文将剖析牛顿法的基本思想和深层含义，并介绍牛顿法的最新进展。

牛顿法的思想

在谈论牛顿法扑朔迷离的历史后，我们再次写下本文上篇给出的由辛普森发明的单变量方程牛顿迭代法：

(1)

我们可以用现在成熟的微积分观点来探讨牛顿法的深层含义。

把一个最一般的非线性方程组写成算子方程 f(x) = 0 并假定变元 x 是个 * n* 维向量，而 f(x) 的值是个 m 维向量。如果这个方程组是正方形，也就是方程个数 m 等于变量个数 n， 那么当今教科书中的牛顿法就是辛普森的版本：

(2)

其中 J(xk) 是 f(x) 在 xk 点的雅可比 (Carl Jacobi，1804-1851) 矩阵，而 ( )-1 表示方矩阵求逆。读者可以发现，如果是单个方程单个变量，这个牛顿法的辛普森公式就回到单变元情形（1）。

关于牛顿法的大部头专著汗牛充栋，其实就像众多伟大发现一样，它背后的道理非常简单易懂。算法（2）的核心思想来自牛顿 - 莱布尼茨微积分理论中最基本的发现：如果函数 f 在 x0 点二次连续可微分，那么，算子 f 在 x0 点附近可以用线性算子二阶近似：

（3）

这里 表示这个近似的误差在渐近意义下是 x 到 x0 之间距离的平方。如果迭代点 x0 很靠近所要求的解 x*，那么原方程组 f(x) = 0 就可以用线性方程组：

（4）

来近似代替，其解 x=x1 就是公式（2）取 *k=*0。于是也就不难理解在极限情形 x1 的精度是 x0 精度的平方，精确数位加倍，也就是所谓二阶收敛。

我们可以通过几何作图来理解经典牛顿法的思想。在直角坐标平面上，单变元方程 f (x) = 0 的解 c 是函数 y = f (x) 图像与 x 的截距。取 c 点的初始近似点 x0，在 f (x) 图像上对应点 (x0, f (x0)) 处作一条切线，这条切线就是函数 f (x) 的线性近似 f (x0)+ f’(x0)(x-x0) 。用这个线性近似代替原函数求零点，也就是求切线的 x 截距 x1 = x0 – f (x0)/f’(x0)。只要 x0 取在 c 点的附近，显然 x1 就更靠近解 c。重复这个过程直到无穷就得到近似解的一个序列 {xk}，由 (1) 式给出，它最终收敛到那个精确解 c。

图 1：牛顿迭代法图示

收敛三要素

从这个基本思想出发，我们也很容易看出牛顿法适用的三个条件：

(1) 函数 f 的光滑性，也就是在解的附近二次连续可微。

(2) 解 x* 的正则性，也就是雅可比矩阵在 x* 点可逆。

(3) 初始近似的局部性，也就是 x0 距离 x* 不太远。

其中光滑性保证线性近似（3）成立，局部性保证迭代（2）收敛到解，而正则性不仅保证线性方程（4）唯一可解，同时意味着所求的解 x=x1 是个孤立点。这正则性保证解的孤立性来自数学分析重要的定理之一的逆映射定理。

从上面的分析看出，牛顿法的三个条件极其自然，似乎缺一不可。没有光滑性或局部性，线性近似（3）及迭代收敛就无从说起。没有正则性，那么公式（2）中的逆矩阵就成问题。另一方面，牛顿法的成就又在于，只要这三个条件就足够了。

参考文献 [1] 提到，傅里叶 1818 年和柯西 1929 年发表的文章从理论上证明了单变元单个方程牛顿法（1）在三个条件下的二阶收敛性。而现在的共识是牛顿法（2）的最完整的收敛理论归功于前苏联数学家康托若维奇 (Leonid Kantorovich，1912-1986) 发表于 1939 年和 1948 年的两篇文章。目前看来，这些文章的收敛性定理表述都有些过于艰涩，其实就是一句话：在上述三个条件下，牛顿法保证二阶收敛。

由于康托若维奇完善了收敛理论并把牛顿法进一步应用到无穷维巴拿赫空间，某些文献也把牛顿法称为牛顿 - 康托若维奇方法。于是牛顿法的冠名争议案子又增加了一个。

超定方程组的高斯 “救场”

包括很多专家在内都有一个流传广泛的误解，以为一个方程组的方程个数必须跟变量个数一样多。这个误解恐怕来自教科书，因为计算数学教科书基本上只谈这类方程组。**只有专家读的专著才会谈到，方程个数大于变量个数的方程组称为超定方程组，反之称为欠定方程组。事实上，正方形的方程组虽然有很多理论和求解的方便，但是很多问题本质上就是超定或欠定方程组，在科学计算中根本不可回避。**对于超定或欠定非线性方程组，相应的线性近似方程组（4）也是超定或欠定，雅可比矩阵的逆矩阵别说去计算，连定义都没有。怎么办呢？十分遗憾，通用教科书里基本上是找不到答案的。

高斯（Johann Carl Friedrich Gauß , 1777-1855）也是无需介绍的伟大数学家。数学史上一个里程碑式的定理叫代数基本定理，也就是说多项式方程必有复数解。历史上众多数学巨匠尝试过证明这个定理，后来发现都差得远呢。这些大师包括达朗贝尔、欧拉、拉格朗日和拉普拉斯，可谓 “江山如此多娇，引无数英雄竞折腰”。最终是谁证明了代数基本定理也是个众说纷纭的数学传奇。高斯 1799 年把这个世纪难题当博士论文做了，一般被认为是第一个正确的证明。高斯尽管在数学上的成就辉煌，最让人津津乐道的故事却是在他七岁上学后的第二年，老师显然是热衷题海战术，让全班练习从 1 加到 100，神童高斯哪里有兴趣去死加一百个数，跟老师说，1+100=2+99=3+98=101， 结果不就是 101×50=5050 吗？他老师是如何吃惊就不难想象了。

1809 年，“数学王子” 高斯第一个将牛顿法推广到超定方程组。在数值求解超定方程组（4）时，雅可比矩阵 J (x0) 不是方阵，而是一个高矩阵，其逆没有定义，当然也就推导不出牛顿法。然而数学王子发现了一个看似不起眼的妙招，当雅可比矩阵是列满秩，即它的秩等于列的个数时，牛顿法可以再度推广到超定方程组：用矩阵的左逆代替传统逆矩阵就行了。

一个可逆矩阵 A 的逆矩阵 A-1 左乘和右乘 A 的结果都是单位矩阵 I。但当 A 的行数和列数不相等时，此事永远不会发生。而当 A 的秩等于它的列数时，则存在矩阵 B，其左乘 A 的乘积 BA 等于单位矩阵 I。这个矩阵 B 称为 A 的左逆，它的理论表达式就是矩阵 B=(ATA)-1AT，其中 ( ) T 表示矩阵转置运算，也就是说以横的行转过来变成竖的列。用 J (x0) 的左逆左乘（4）式两边然后解出 x，高斯将牛顿迭代修正为 “高斯 - 牛顿迭代”：

(5)

要知道常规逆矩阵也自动是左逆，因此辛普森的牛顿法公式 （2）变成了是高斯公式（5）的特例。

高斯 - 牛顿法常常也简称牛顿法。于是牛顿法的适用范围从方形方程组扩展到包括超定方程组。由于超定方程组通常不存在通常意义的解，这种情况下高斯 - 牛顿法可以求出一个推广意义下的解，称为最小二乘解。这是高斯留给应用数学和计算数学的遗产。可惜它埋没于优化类专业书籍里面，多数计算数学通用教科书上不提。

值得一提的是，牛顿法的二阶收敛并不是最快的求根计算方法。比较著名的三阶收敛迭代法有哈雷（Halley）迭代和拉盖尔（Laguerre）迭代，也就是每步迭代获得的精确数位是前一步的三倍。作为课外练习，数学专业本科生都可以构造任何有限阶收敛的快速迭代法。然而从实际计算的角度来看，超过二阶收敛的迭代法仅仅在解决特定问题上可能有些价值。作为通用算法，简单得不能再简单的牛顿法已经二阶收敛，其实际效率在计算中很难被真正超越。哈雷先生虽然以首次算出哈雷彗星轨道周期名垂科学史，但他的迭代法基本上沦落到被遗忘的角落。在此也希望年轻学者不要在研究通用高阶收敛迭代法的问题上浪费时间。除非找到特定应用，超过二阶的收敛速度一般没有实际意义。

进一步的探讨

一个科学发现常常只能被幸运地发现一次。牛顿法则是一次次被重新推广和修正，每次新发现的结果是，我们原来知道的牛顿法不过是新版的特例而已。

从巴比伦 - 赫伦求平方根扩展到韦达 - 牛顿 - 拉夫森的多项式求根， 扩展到辛普森公式求解超越方程和方形方程组，再扩展到高斯求解超定方程组，再扩展到康托若维奇在巴拿赫空间求解，看似简单的 “牛顿法” 几千年来一再被赋予新的内涵，扩展到更广泛的应用。这期间还引出众多数学大师如傅里叶、柯西和拉格朗日。**牛顿法的发展和演变历史，也是数学学人不断探索新领域解决新问题过程的写照。牛顿法的奇妙还在于，从诞生以来一次次的发展、推广和创新都是实质性的，而不仅仅是修边角式的改善。**牛顿之后的每次推广都远远超越牛顿的初等方法。当然所有的推广都被习惯性地称为 “牛顿法”。于是，“经久不衰的迷思” 成为传统。

随着电子计算机的出现以及随之而来的计算数学这一学科的诞生，牛顿法作为求解非线性代数方程组的基本通用方法在科学计算的大舞台上大显身手，到处都是其用武之地。由于解方程的问题太常见，对各种迭代法的深入探索和进一步推广从来没有停止过。要想从牛顿法有所创新，三个收敛条件（光滑性、正则性和局部性）是显而易见的入口。

光滑性，也就是函数或映射 f 连续二阶可微在绝大多数实际应用中不成问题。对于导数不存在、无法求导或者雅可比矩阵计算成本太高的特定方程，可以使用拟牛顿法和创新不动点迭代。这基本上超出了牛顿法的范畴，在此就不多谈了。无需微分的算法难以利用微积分的线性逼近，因此都未能达到二阶高速收敛而无法成为通用算法。

局部性，也就是初始迭代点 x0 取在所求解的一个局部邻域则牛顿法必定收敛。这常常被人误以为是牛顿法的一个弊病。局部收敛的对立面是所谓全局收敛（global convergence），也就是从定义域内的任何初始点出发都保证迭代收敛到一个解。全局收敛算法只存在于求解特定问题的特定迭代。

比如说，巴比伦算法在求平方根这个特定问题上就是全局收敛。在发现全局收敛的通用迭代法之前，牛顿法的局部收敛性在一般问题上不输任何算法，所以很难说局部收敛是牛顿法的弊病和短板。局部收敛更恰当的说法是牛顿法的一个特性。由于一般方程组 f(x) = 0 的解可以不唯一，即使找到全局收敛算法，从常理上说这个潜在算法也应该具有局部收敛性，否则无论如何靠近一个解都会跳到另一个解，这算法真能用吗？

欣然接受牛顿法的局部收敛特性并加以利用，可以构造出各种全局收敛算法解决特定问题。一个成功的项目始于 1976 年，第一篇现代同伦延拓法的文章横空出世，作者之一就是笔者的博士导师李天岩（1945-2020）教授。现代同伦法的进步在于结合微分拓扑和代数几何思想对计算数学领域的渗透。将这些思路与牛顿法相结合，构造出的目前效率最高、速度最快的求解方法和软件适用于多项式方程组。

常有人说数学是艺术，意思多半是说数学本身是艺术，看你有没有能力欣赏。读者可能想不到，牛顿法的局部收敛特性还可以用来创作似乎毫不相干的艺术作品。无论是什么世界名画，油画在数学上无非是每个点都有一个颜色，而每个颜色都可以换算成三个数字代表红黄蓝三原色的强度，反之亦然。任何数学方法，只要能给每个点赋予一个或三个数字，这个方法就可以用电脑做出一幅油画，只要发挥想象力创造力，创作可能性是无穷的。

为激发起学生的兴趣和灵感，笔者之一每次教计算数学课都给学生出个简单的计算实验题目：凭你的想象找一个函数 f ，一个复平面区域，一个小数 ε 和一个大数 M。把区域划分成细密的网格，从每个网格点出发启动牛顿法求解 f(x) = 0 。如果在 M 步内收敛到某个点的 ε- 邻域，用 |xk-xk-1|＜ε 作为判断准则，则该网格点就赋予第 k 号颜色。如果 M 步内不收敛，该网格点就保持空白。计算完成后，用随机数产生 M 种随机颜色给每个网格点按号码 k 涂上颜色，结果就是一幅牛顿油画。题目一出，以为数学枯燥的学生们立马兴致盎然，纷纷尝试各种函数做出五花八门、五彩缤纷类似下面的牛顿油画。这类数学作画方法在高端瓷砖设计和服装印花等行业还真有很大应用前景，画出名家都意想不到的作品。

图 2：分别用复函数 $f(x)=sin(cos(x))$, sin (x3-1) 和 x (x3-1) 2 做出的牛顿油画

回到 “正则性”

至于牛顿法的正则性（regularity）条件，那更是大有文章可做了。

用通俗语言说，一个问题是正则的最一般的定义是，这个问题的解的变化上界跟问题数据扰动大小成比例。用数学语言说的话就是，问题的解利普希茨（Lipschitz）连续依赖于数据。

正则性是数学上的一个重要性质。在计算数学里更是重要到不可或缺的程度。可以说计算数学只能解决正则问题。非正则的问题又称为奇异（singular）问题。奇异问题跟数值计算水火不容。所以在计算数学教科书上基本上找不到任何奇异问题的数值解法。因为教科书上没说，一个秘密就有点鲜为人知：奇异问题常常可以正则化。至于怎么正则化，那就是施展聪明才智的时候了。寻找正则化方法，探索奇异问题的数值解是计算数学尚未充分开发而又前景广阔的处女地。

满足正则性的方程解必定是孤立点。而奇异解可能是孤立的重根，但更常见的情形是方程组的解是个高维流形，比如曲线和曲面，这些都属于所谓非孤立解。非孤立解在科学计算中十分常见。很多应用问题的关键就在奇异点上。回到牛顿 - 莱布尼茨微积分的基本思路，要求解非线性方程组 f(x) = 0 ，先把方程转换成线性逼近方程（4）。由于雅可比矩阵在解点奇异，不存在逆矩阵。要想扩展牛顿法，可能的突破口就在矩阵求逆。信手拈来有个广义逆矩阵。

广义逆矩阵的始祖，是一百年前的美国领头数学家之一穆尔（Eliakim Moore，1862-1932），他于 1920 年提出了这个概念，并用正交投影的方式定义了它。2020 年诺贝尔物理奖得主、英国数学家彭罗斯（Roger Penrose）于 1955 年漂亮简洁地用四个等式独立给出了穆尔广义逆的等价定义。给定矩阵 A，现在被称之为 A 的穆尔 - 彭罗斯广义逆通常记为 $A^{†}$ 。前面提到高斯用到的左逆就是 A 为列满秩时的穆尔 - 彭罗斯广义逆特例。逆矩阵存在需要正则条件，而任何矩阵包括奇异矩阵都有广义逆。上个世纪六、七十年代，广义逆领域的名家本 - 以色列（Adi Ben-Israel） 很自然地想到用广义逆代替雅可比逆矩阵，于 1966 年提出广义牛顿法：

(6)

并试图应用于求解奇异方程组。可是问题并不是把求逆上标 “-1” 换成求广义逆上标 “†” 这么简单。它需要一大串莫名其妙的条件才能保证收敛，因此难以成为通用算法。

直至 1982 年，笔者的大师兄朱天照教授首次证明了迭代序列 (3) 对雅可比矩阵行满秩欠定方程组的局部收敛性。到了九十年代，在香港任教的陈小君和祁力群教授用更广义的所谓 “外逆” 取代穆尔 - 彭罗斯广义逆，在某些条件下证明了使用某种特殊外逆的牛顿法二阶收敛到一个驻点，然而不能保证驻点是解。例如，高斯牛顿法（5）形式上是广义牛顿法（6）在超定方程组的特例。而高斯牛顿法（5）收敛到的驻点只能保证满足最小二乘解的必要条件，一般来说不是 $f(x)=0$ 在通常意义下的解。

最新发展

问题的瓶颈在哪里呢？广义逆的一个特性是在奇异矩阵附近不连续，稍加扰动矩阵就成为坏条件可逆矩阵，所以在奇异解附近，广义牛顿法（6）退化成辛普森牛顿法（2），直接使用广义逆仅仅是把求解方程的奇异问题换成广义逆矩阵的奇异问题，并没有跳出奇异怪圈。再一个短板在于，正则解只有一种，奇异解的奇妙在于各有各的奇异性。企图一口吃个大胖子，一个方法横扫一切奇异解，天下哪有这种好事。

找到了问题的关键，思路就成为可能。矩阵的奇异性有个线性代数教科书很少提到的规律：奇异是有方向性的。在任何一个奇异矩阵附近，扰动只可能增加矩阵的秩（rank）而不会减少。任给一个矩阵 A 及其任何一个可能的秩 r， 跟 A 距离最近的那个秩等于 r 的矩阵称为 A 的 “秩 r 投影”，记为 $A_{\text{rank}-r}$ ， 这个投影很容易通过奇异值分解算出。如果 A 的秩是 5， 那么先做秩 5 投影再做广义逆，也就是 $A_{\text{rank}-5}^{†}$ 。利用附近矩阵的秩不可能小于 5 的秘诀， $A_{\text{rank}-5}^{†}$ 不仅在 $A$ 附近连续而且是要求更高的利普希茨连续。于是广义逆不连续的障碍就可以轻松跨过。假定雅可比矩阵在方程组的解 x* 点的秩是 r， 我们就可以用这个思路很自然地提出降秩牛顿法

(7)

其中 $J_{rank-r}{\left(x_k\right)}^{†}$ 是雅可比矩阵作秩 r 投影后的广义逆。有了思路还只是开始，计算数学的奥秘就包括思路可以通过计算实践验证。试算结果证实迭代法（7）神奇般地快速收敛到初始点附近的解曲线或曲面，有戏了！

迭代（7）一旦收敛到某个点 $\hat{x}$，那么 $xk$ 和 $xk+1$ 的极限都是 $\hat{x}$ 并且在等号两边相互抵消，得出，也就是说 $\hat{x}$ 是个 “驻点”，不一定是解，这是本 - 以色列、陈小君和祁力群等学者所碰到的老问题。要跨越这个障碍，还得下点功夫探讨奇异解的本性。

正则解是孤立解，维数是零。雅可比矩阵是满秩，秩损失也是零。秩损失有个专用词，叫零度（nullity）。正则解的维数不多不少刚好等于雅可比矩阵的秩损失这个现象不容易被注意到，因为都是零。非孤立解如果是曲线，则维数是 1，曲面维数是 2，超曲面的维数可以是 3，4 等等。常见的非孤立解有个特性：雅可比矩阵在这些解的秩损失也刚好等于解的维数！换句话说，解曲面的切空间就是雅可比矩阵的零空间。也可以说，通常的非孤立解虽然奇异，但还是恋恋不舍地保留了正则解的一个关键特性。我们不妨把这类奇异解先分离出来，称为半正则解。利用半正则性，就可以证明在半正则条件下降秩牛顿法（7）收敛到的驻点就是解曲面上大致最接近初始迭代点 x0 的一个解点 。

由于一个偶然的发现，降秩迭代（7）再度推广牛顿法。从巴比伦法、辛普森版本牛顿法、高斯 - 牛顿法到朱天照公式，前述所有有限维空间中的牛顿法都是（7）的特例。引文 [2] 中证明，只要映射 f 满足光滑性，所求奇异解满足半正则性和初始点满足局部性三个基本条件，加上投影秩 r 取为雅可比矩阵在解曲面上的秩，则降秩牛顿法（7）二阶收敛到解曲面上最近的解点。不仅如此，降秩牛顿法（7）成为天然正则化机制。奇异解曲面或曲线之所以奇异，在于经不起折腾。在数据扰动下可以大幅跳跃甚至消失殆尽。然而降秩牛顿法（7）仍然在扰动状态下收敛到一个驻点，这个驻点是消失掉的半正则解点的精确近似而且误差上界跟扰动量成比例，于是半正则的奇异性完全被降秩牛顿迭代清除，完成问题的正则化。这个牛顿法的新发展即将在权威期刊《计算数学》上发表（见文献 [2]）。

你如果读到这里会问，如果方程组的解奇异程度超过半正则怎么办呢？那么恭喜你。你已经具有数学研究的基本素质。学无止境。学问学问，会问才能有学问。发现问题是解决问题的开始。发现下一个版本求解超奇异方程牛顿法的没准就是你呢。

读到这里，你不觉得牛顿法神奇吗？

后记： 作者以此文纪念我们的导师李天岩教授（1945 年 6 月 28 日 - 2020 年 6 月 25 日）逝世一周年。

参考文献

[1] T. Yamamoto, “Historical development in convergence analysis for Newton’s and Newton-like methods”, J. Comput. and Appl. Math., 124, 1-23, 2000

[2] Z. Zeng，“A Newton’s iteration converges quadratically to nonisolated solutions too，”to appear in Math. Comput.

---

via：

• “数”往开来 | 牛顿迭代法
  https://mp.weixin.qq.com/s/ZKOnsCiRggvutEdE4bCS1w

• 一口气看完牛顿迭代法（课本中的高数背景）
  https://mp.weixin.qq.com/s/hkJG7-GSwhYmLrUmZ5q3pg

• 牛顿迭代法的可视化详解
  https://mp.weixin.qq.com/s/J0uJiBNhcTyllvrEnXzFxw

• 牛顿迭代法传奇（上）：张冠李戴的命名 原创 曾钟钢、丁玖 返朴 2021 年 06 月 26 日 08:11
  https://mp.weixin.qq.com/s/RSqUQ4a7_NG7QKWFcisTzA

• 牛顿迭代法传奇（下）：意犹未尽，柳暗花明 原创 曾钟钢、丁玖 返朴 2021 年 06 月 29 日 07:52
  https://mp.weixin.qq.com/s/aWoxNepfnuPD0rgzLgAM7w
  —

• 求平方根——牛顿迭代法 | Cao Yi
  https://iridiumcao.github.io/algorithm/sqrt/sqrt.html

• 如何通俗易懂地讲解牛顿迭代法求开方（数值分析）？ - 知乎_
  https://www.zhihu.com/question/20690553