注: 本文为 “尺规作图正十七边形” 相关文章合辑。
感受数学王子高斯的思维
原创 蔡驰南 2024 年 08 月 28 日
数学王子高斯一生有很多惊人的成就,而接下来这个惊人之作,其价值不可估量,因为它让高斯坚定了走数学之路,而不是成为一个语言学家。这是人类之幸。
高斯还是哥廷根大学新生的时候(距离他 19 岁生日还有一个月),仅用了一夜就解决了一个困扰几何学家两千年的难题:用尺规画出正十七边形。
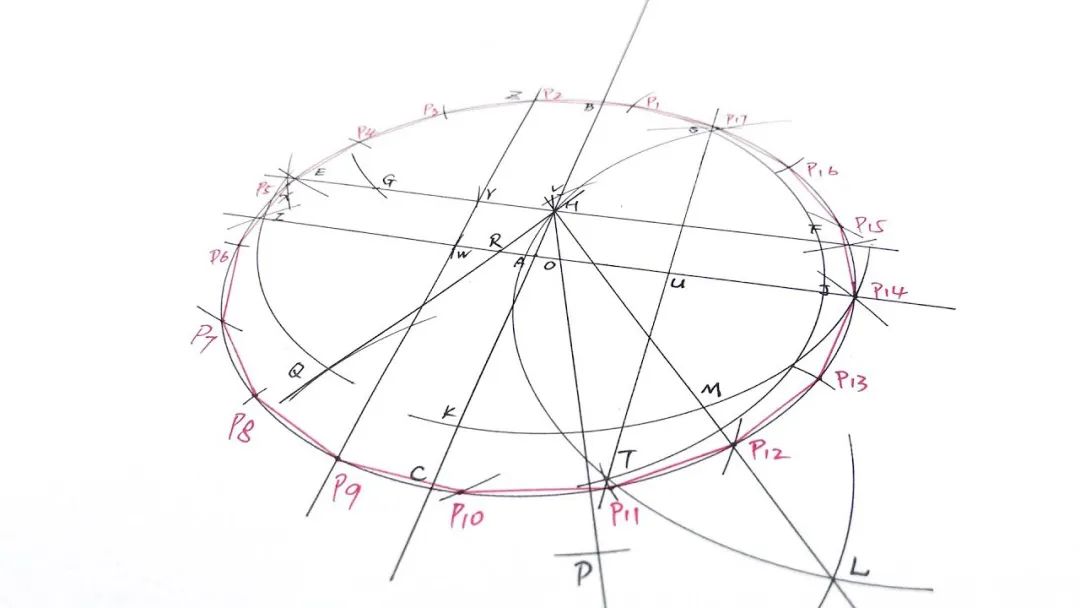
虽然这个问题的确是在1796 年 3 月 30 日解决的,但高斯在日记中记录,之前几个月的时间里,他一直在思考一些数论问题,而这恰恰是关键。高斯为了纪念自己的发现,从那天开始连续记了 18 年的数学日记(Mathematisches Tagebuch)。
他并没有写出尺规作图(没有刻度的直尺和圆规)的具体步骤,而是用数论的方法证明了为什么能用尺规画出正十七边形。当然他肯定知道怎么作图,否则也无法解决这个问题了。
在此之前笛卡尔就有论文很清楚地说明了:给定单位长度后,如何用几何方法把线段的长度加减乘除以及开平方。(笛卡尔在 1637 年发表了一篇著名的数学论文《几何学》(La Géométrie),探讨了利用代数手段解决几何问题的方法。)
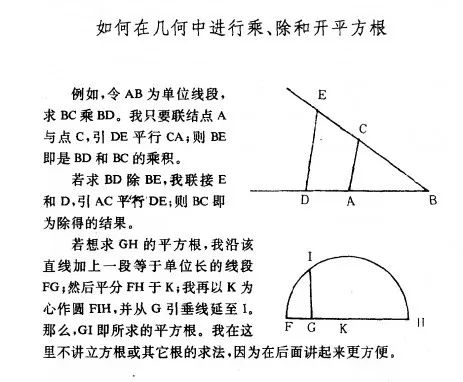
那我们就来看看高斯究竟是怎么做的。
其实高斯只做了一件事,就是找到 cos ( 2 π 17 ) \cos \left( \frac{2\pi}{17} \right) cos(172π) 的只含二次根式的表达式。
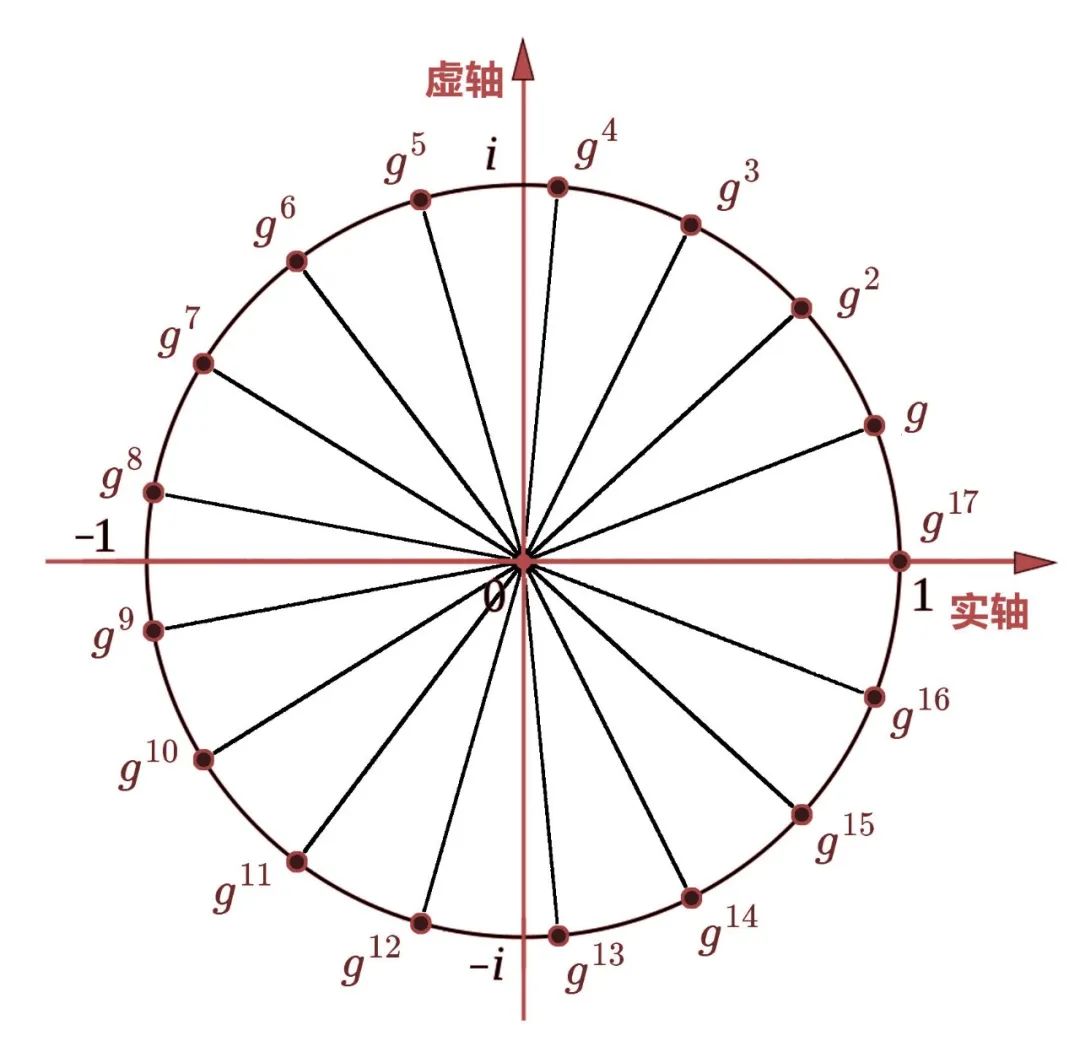
对于方程 x 17 − 1 = 0 x^{17}-1=0 x17−1=0 在复平面上共有 17 个根,它们呈单位圆上的十七等分。
我们假设 g = cos ( 2 π 17 ) + i ⋅ sin ( 2 π 17 ) g=\cos \left( \frac{2\pi}{17} \right)+i \cdot \sin \left( \frac{2\pi}{17} \right) g=cos(172π)+i⋅sin(172π),那么其中 16 个根,恰好就是 g g g 的 1 次方到 16 次方,而第 17 个根就是 x = 1 x=1 x=1,也可以说是 g g g 的 17 次方。
x 17 − 1 x^{17}-1 x17−1 可以这样被因式分解:
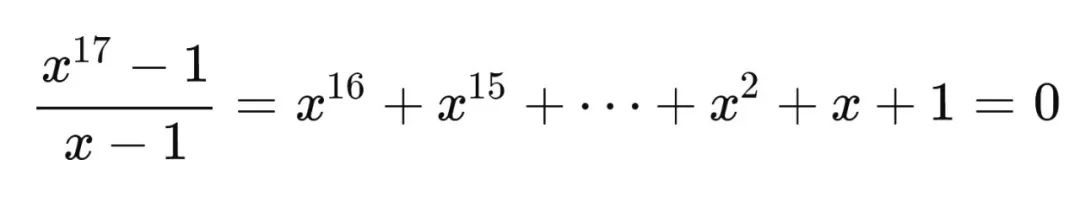
因为 g g g 是上述分圆方程的一个根,所以用 g g g 代入 x x x 等式成立,可得:
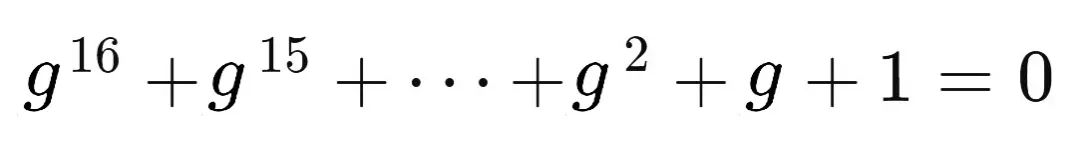
也即:
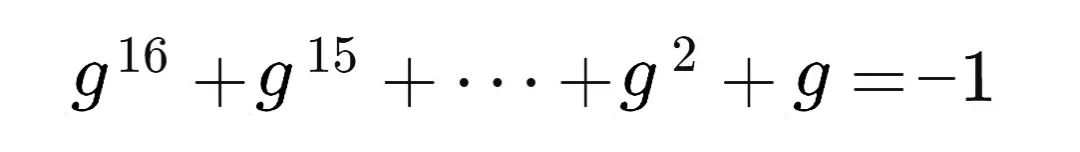
接下来高斯就要开始他的表演了:
将剩下的 16 个根按以下分成 2 组:
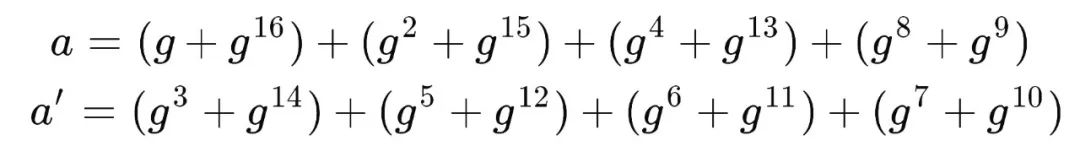
由于这两组内的根(每个括号内的两个根)都两两形成共轭。
什么叫共轭,就是两个复数关于实数轴对称。
所以他们相加,虚数部分就抵消了,而相乘也正好等于一个实数。
a + a ′ a + a' a+a′ 即 g g g 的 1 次方到 16 次方之和,所以 a + a ′ = − 1 a + a' = -1 a+a′=−1。
而根据分组 a a ′ aa' aa′ 的 64 项,恰好 g g g 的 1 次方到 16 次方各出现了 4 次(别忘了 g g g 的 17 次方等于 1,可以将所有项都降到 16 次方以内)。
所以 a a ′ = − 4 aa' = -4 aa′=−4。
根据 韦达定理 可知, a a a 和 a ′ a' a′ 就成了新方程 x 2 + x − 4 = 0 x^2 + x - 4 = 0 x2+x−4=0 的两个根。
运用二次方程求根公式,显然 a a a 和 a ′ a' a′ 都可以表示成二次根式的形式。
然后将 a a a 和 a ′ a' a′ 再次分组,得到 b b b 和 b ′ b' b′,以及 c c c 和 c ′ c' c′。

接下来再将 b b b 分成 d d d 和 d ′ d' d′。
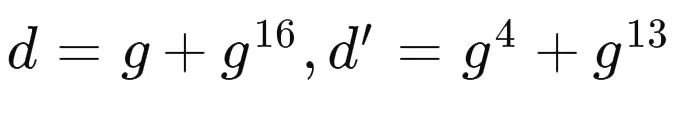
可知 d d d 和 d ′ d' d′ 就是方程 x 2 − b x + c = 0 x^2 - bx + c = 0 x2−bx+c=0 的两个根,又知:
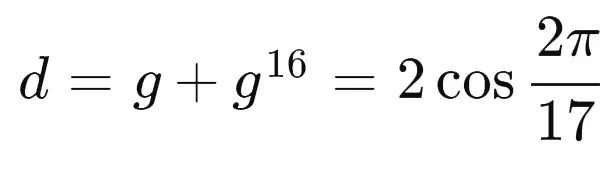
由上面的一系列分组我们知道, a a a 和 a ′ a' a′ 可以表示为二次根式的形式:
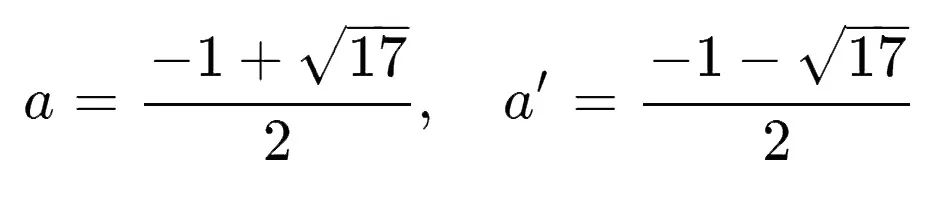
而用相同的方法可知: b b b、 c c c、 d d d 也都可以表示为二次根式嵌套的形式:
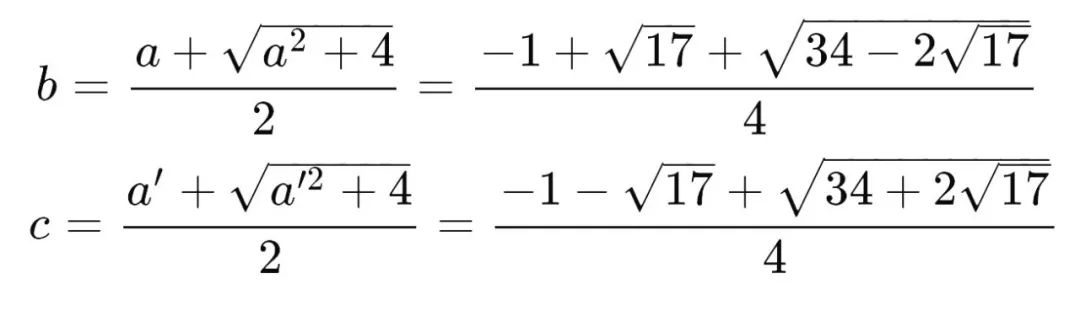
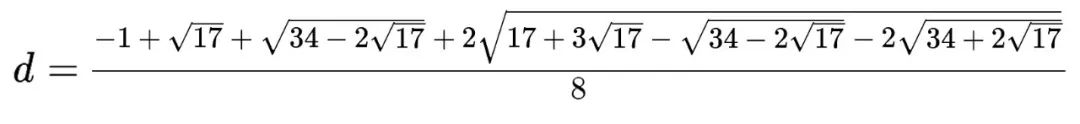
那么我们就得到了最关键的 cos ( 2 π 17 ) \cos \left( \frac{2\pi}{17} \right) cos(172π) 的表达式:
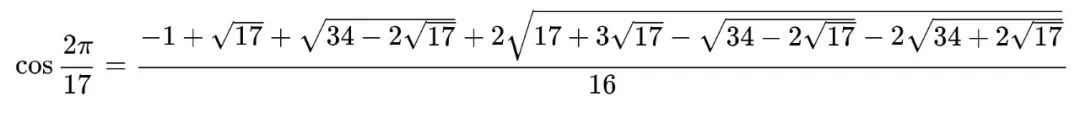
所以,任意给出一个单位长度,我们就能得到 cos (2π/17) 的长度,进而得到单位圆中 2π/17 的角度,那么正十七边形问题就迎刃而解了。
所以,任意给出一个单位长度,我们就能得到 cos ( 2 π 17 ) \cos \left( \frac{2\pi}{17} \right) cos(172π) 的长度,进而得到单位圆中 2 π 17 \frac{2\pi}{17} 172π 的角度,那么正十七边形问题就迎刃而解了。
高斯不仅解决了正十七边形问题,还找到了能用尺规作图的正多边形需要满足的条件。
从这个问题的逻辑链,我们可以感受到高斯的思维深度。他将自己的这个惊人发现写进了数论大作**《算术研究》**里,成为了那部著作的压轴大戏。
高斯完成了用数论方法解决几何问题的壮举,这种不同数学分支间的联系,往往具有重要价值。
高斯的确是一位思想深刻,出手不凡的天才,可即便强如高斯,也告诉了我们一个道理:惊人的成就绝不可能一蹴而就。
高斯在 1801 年证明了如果费马数 K K K 为质数,则可以用直尺和圆规将圆周等分为 K K K 等份。基于这一结果,高斯成功作出了正十七边形。高斯进一步提出,一个正多边形可以用直尺和圆规作图的充分条件是其边数 n n n 是 2 2 2 的幂次与若干费马素数的乘积。虽然高斯认为这是必要条件,但未能提供证明,后来由 Pierre Wantzel 给出证实,因此这一结果被称为“高斯 - Wantzel 定理”。
为什么只有边数为费马素数的多边形才能用尺规作图
朴正欢 zhihu
确切地说是边数为 2 的幂与费马素数之积的正多边形可用尺规作图
首先,作正 n 边形等同于在复平面上作 n 次单位根
使用圆规和直尺相当于分别在平面上构造二次方程和一次方程,反复使用尺规即在平面反复嵌套和这两种方程并求解的过程,因此可以用尺规作图的数是最高次数为 2 的幂且在 Q 中不可分解的多项式的根
且对任意可构造的数构成的域 K, [ K : Q ] = 2 m [K:Q]=2^m [K:Q]=2m ,即 K 作为 Q 上的线性空间维度为 2 的幂
由 n n n 次单位根的定义易知其在 Q Q Q 上的维度是 ϕ ( n ) \phi(n) ϕ(n),事实上它们是 x ϕ ( n ) + . . . . + 1 = 0 x^{\phi(n)}+....+1=0 xϕ(n)+....+1=0 的根
而 ϕ ( n ) = 2 m \phi(n)=2^m ϕ(n)=2m 的数是 2 的幂与费马素数之积
发布于 2014-01-15 02:18
黄金时代的群山之巅
*原创 蔡驰南 2024 年 08 月 22 *
19 世纪是数学的黄金时代,这一百年里新增的数学成果超过了之前所有时代的总和。
如果将这个时代的数学家比作群山,那群山之巅无疑要数卡尔・弗里德里希・高斯(Carl Friedrich Gauss,1777 年 4 月 30 日 —1855 年 2 月 23 日),一位基本靠自学成才的天选之子。自他之后,数学的中心开始由法国向德国倾斜。

可以说数学上的惊人之举贯穿了他的一生。
高斯出生于德国布伦瑞克的一个贫寒之家,他对数字很敏锐,仅仅通过自己的观察就学会了计算,三岁时已能纠正父亲账目上的错误。

德国布伦瑞克
高斯 10 岁时,老师在课堂上出了一道题,让学生计算从 1 加到 100,还没等老师坐下,小高斯就心算出了答案。在没有任何人指导过的情况下,他自己摸索出了等差数列快速求和的方法。
从此,他的老师比特纳和助手巴特尔斯意识到了这个孩子天赋异禀,很快就让布伦瑞克 - 吕讷堡公爵(卡尔・威廉・斐迪南,布伦瑞克 - 吕讷堡公爵,布伦瑞克 - 沃尔芬比特尔 - 贝芬亲王,Charles II William Ferdinand, Duke of Brunswick-Lüneburg, Prince of Brunswick-Wolfenbuettel-Bevern)注意到了高斯的才能。

布伦瑞克 - 吕讷堡公爵
这位具备学识教养且仁厚开明的公爵见了高斯,十分欣赏,从此开始资助高斯。高斯顺利完成了在本地卡罗琳学院的学习后,被哥廷根大学录取(1795 年)。
然而进了大学的高斯困惑于,自己究竟是学习语言还是学习数学。

哥廷根大学
距他 19 岁生日还有一个月时(1796 年 3 月 30 日),高斯终于不再迷茫。他在那一天解决了一道困扰数学家近两千年的难题:用尺规画出正十七边形,并证明了用尺规能还画出哪些正多边形。
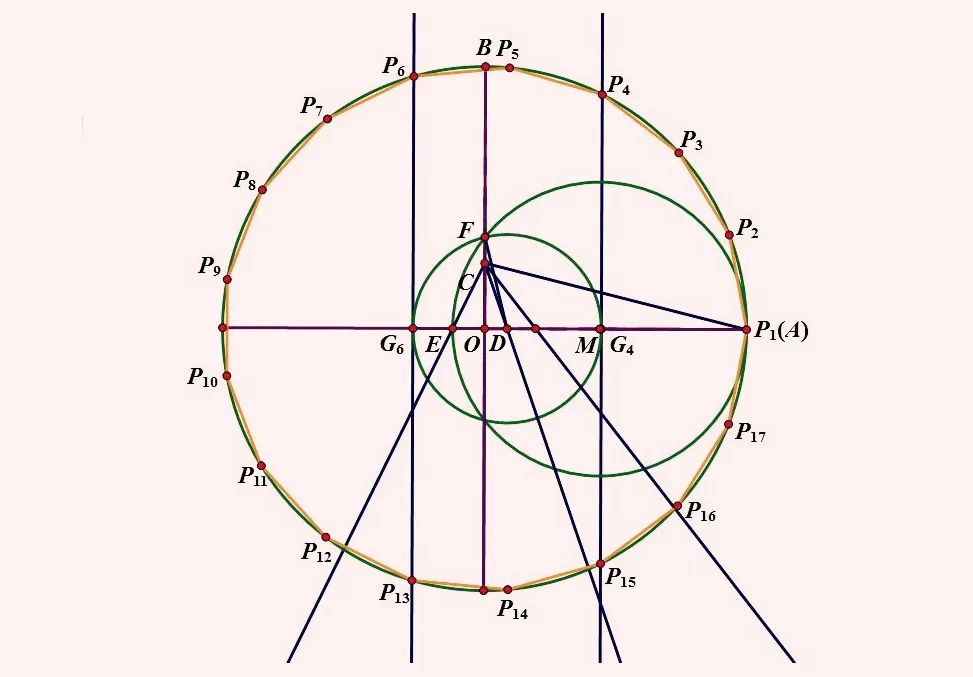
从此,高斯选择了数学,这是人类之幸。
之后他开始记日记,以纪念这次重大发现,而他的日记一直持续了 18 年。仅仅这一年(1796 年),他的数学日记(Mathematisches Tagebuch)里就有许多惊人的发现:
3 月 30 日,构造正 17 边形的方法;
4 月 8 日,二次互反律的第一个证明;
5 月 13 日,猜测素数分布的规律即素数定理;
7 月 10 日,提出任何自然数是最多三个三角形数的和,“ΕΥΡΗΚΑ!num =Δ+Δ+Δ”。
还在读大学的高斯开始撰写数论著作。
在 21 岁时(1798 年)他完成了巨著**《算数研究》**。这一年,高斯博士毕业,再次回到了家乡布伦瑞克。
在公爵的资助下,3 年后(1801 年)该书出版。

在书中,高斯建立了同余的概念和符号;对 18 世纪数论成就进行了回顾;提出了 “黄金定理”二次互反律的证明(两年前勒让德的证明存在漏洞);他在全书最后,讨论了分圆多项式和尺规作图问题,原来当年的几何难题归根结底是一个数论问题。
拉格朗日看后,写信给年轻的高斯说:“你的《算数研究》一书,已使你跻身于第一流数学家之列了。” 然而,这本书真正受到重视,已是二十余年之后。
回到家乡,没有找到教职工作的高斯,不愿一直接受公爵的资助。于是放弃了纯数学研究,选择成为专业的天文学家。

最早让高斯声名大振的是天文学,而非数论。
1801 年,天文学家(皮亚齐)发现了新的小行星谷神星,但是几周之后,这个小天体被跟丢了。高斯借助最小二乘法,设计了 “高斯法”,仅凭三次观测,就计算出了星体的椭圆轨道(现在仍然用于最终未卫星)。天文学家按高斯的预测去寻找,果然再次发现了谷神星。
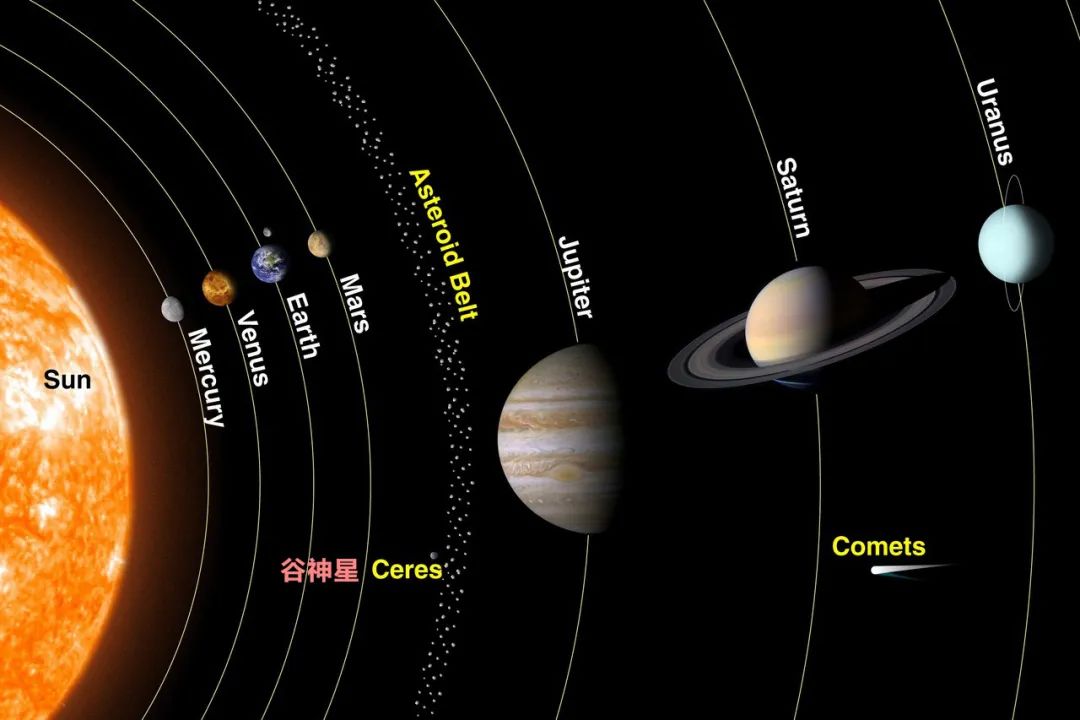
24 岁的高斯一战成名,俄国获悉后,曾一度想邀请高斯去圣彼得堡接替去世的欧拉。
德国意识到了高斯的重要性,在各方人士努力之下,哥廷根新建了一座天文台,邀请高斯担任天文台台长(1807 年)。高斯在那里出版了**《天体运动论》**。

哥廷根天文台
大约 15 年之后,他开始负责汉诺威全境的勘测,历经多年,他不但完成这项艰巨的任务,还凭借非凡的智慧洞悉了球面几何的本质,并创造性地提出了高斯曲率,一个影响到广义相对论和宇宙形状的数学概念,高斯称之为 “绝妙定理”。

他因此出版了著作**《曲面的一般研究》**(1827 年),标志着新的数学分支 ——微分几何的创立。

高斯在辞去天文台的工作后,又投身电磁学的研究。他与韦伯合作,创造了世界上第一个电话电报系统(1833)和第一张地球磁场图(1840)。

高斯与韦伯
高斯不经意间的一个发现,可能就为后世研究的出发点。
他将复数以复平面上点的形式进行呈现,这种可视化让虚数开始被普遍接受,现在的复平面也被称为高斯平面。

他在处理了足够多的天文数据后,得到了具有概率性质的测量结果,提出了正态分布(高斯分布),这也是概率论中最常见的一种分布。
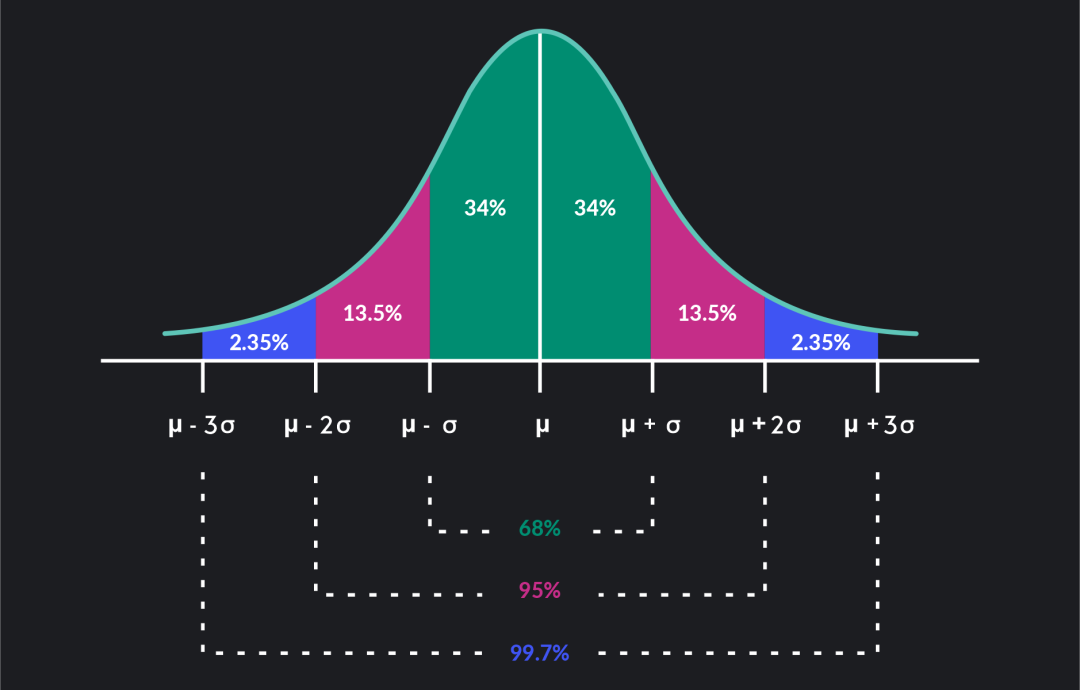
高斯是一位完美主义者,如他自己一直信奉的格言 “少而精”,未经过深思熟虑,从不轻易示人。正因如此,他有很多重要的发现,一生都未发表。
笔记显示,他对非欧几何和椭圆函数论都有深刻认识。
19 世纪上半叶,高斯未发表的内容,成为悬在数学界头顶上的 “达摩克里斯之剑”。数学家们深怕自己毕生研究的成果,高斯在几十年前就已经得到了结论。
高斯是一位生在黄金时代的天才,他的成就涉及数学的各个方面,甚至还开辟出了很多新的分支,深刻影响了人类上百年的历史。
身处群山之巅的高斯却谦虚地说道:“假如别人和我一样深刻而持续地思考数学真理,他们也会作出同样的发现。”
via:
-
为什么只有边数为费马素数的多边形才能用尺规作图? - 知乎 发布于 2014-01-15 02:18
https://www.zhihu.com/question/22102950 -
正十七边形的尺规作图 2020-02-06 15:59:40
https://www.bilibili.com/video/BV157411h7Et/ -
感受数学王子高斯的思维原创 蔡驰南 蔡爸谈数学 2024 年 08 月 28 日 12:34 上海
https://mp.weixin.qq.com/s/9VkfUgfXyauHnnebvrKsvA -
黄金时代的群山之巅 原创 蔡驰南 蔡爸谈数学 2024 年 08 月 22 日 12:33 浙江
https://mp.weixin.qq.com/s/qTeIyPHF6J9n4CNQCMTeHg

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








