注:本文为 “红黑树” 相关文章合辑。
未整理去重,如有内容异常请看原文。
Red-Black Tree / 红黑树
AWN
Feb 7, 2020

from Beenabug44 on pixabay.com .
树的搜寻 (Tree Search),一直是电脑科学领域的重要算法,当中探讨了树可能遇到的问题:树成长时可能偏重于特定一边,即不平衡 (Unbalance) 的现象。二元树是常见且广泛使用的一种树,面临这样关乎运气、可能退化成连结串列 (Linked List) 的潜藏缺点,在使用上免不了让人担心效能是否能常保顺畅。此外,在一些应用上,可能不期望这样不平衡的可能性发生,所以具有自动平衡左右数量分布效果的算法早在约 1962 年便被发表出来,称为 AVL 树 (Adelson-Velsky and Landis Tree, AVL Tree)。这种平衡成长的二元搜寻树 (Binary Search Tree, BST) 被归类称为自平衡二元搜寻树 (Self-Balancing Binary Search Tree)。
接下来,要介绍同归为自平衡二元搜寻树的红黑树 (Red-Black Tree, RBT or RB Tree) 对平衡性的要求比 AVL 树还宽松。红黑树是利用节点颜色来检视二元树每条延展的路径高度是否差不多,因此发明者订立了以下几点规则:
- 树上的每个节点 (node) 只能是红色或黑色
- 根节点 (root) 一定要是黑色
- 叶节点 (leaf) 一定要是黑色的空值 (NULL)
- 红色节点的两个子节点 (child) 一定要是黑色 (亦即不能有两个红色节点相连,注意:黑色节点的子节点颜色没有限制)
- 从任何节点出发,其下至叶节点所有路径的黑色节点数目要相同
满足上述规则的二元树,相比一般的二元树更能保持平衡性,往后套用二元树的算法来查找资料时能更快速、方便地到达目的地,套用运算的时间复杂度为 O(log n),这是因为红黑树保证最长路径不会超过最短路径的两倍。
因为红黑树也是二元树的一种,所以例如:新增节点、删除节点、查询节点等针对红黑树的操作与二元树的操作前段算法相同,只是在每次操作完毕之后可能会让树的结构改变而可能无法满足成为红黑树的性质,进而可能不具有平衡的性质。为了在操作后仍是一棵红黑树 (满足上述五项规则),以下有两项基本运算可以用来帮助调整树状结构以满足红黑树的规则,这两个运算分别为变色与旋转 (左旋、右旋)。
复习小教室:Operations on Binary Search Tree
- 常见的操作包含:SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR,其中搜寻节点(Search)、找最大节点(Maximum)、找最小节点(Minimum)较单纯,不多介绍。这边想多着墨于找寻上位者(Successor)与下位者(Predecessor)的操作上,这与之后新增(Insertion)与删除(Deletion)节点的操作具有高度关联:
Successor(z):寻找数列的下一个数字 (下位者)。如果右子树非空,则找右子树中最小的节点;如果右子树为空,则往回找第一个比自己大的祖先。
Predecessor(z):寻找数列的上一个数字 (上位者)。如果右子树非空,则找右子树中最大的节点;如果右子树为空,则往回找第一个比自己小的祖先。
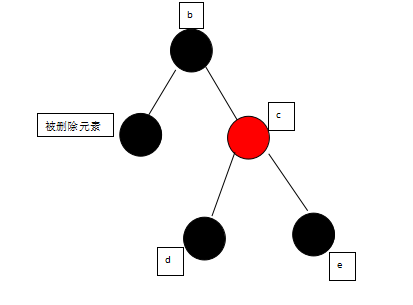
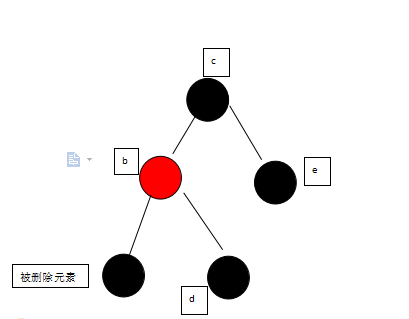
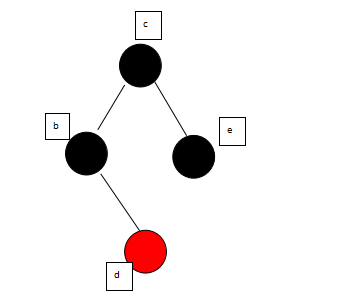
Deletion(z):删除特定节点,由子节点的三种情况来讨论算法。没有子节点或只有一个子节点的时候,直接将该节点删除,其父节点则直接连接至其子节点(或为NULL)上。但有两个子节点时,则需要先找到欲删除节点的下位者是谁,将下位者与欲删除节点的数值交换,再将下位者(已换成欲删除节点数值)删除,其中会将下位者的父节点与下位者的子节点相连
(有两个子节点时,一般是以右边最小的子节点、或者左边最大的子节点来递补)。
首先是变色,这个运算很容易理解,就是将当前颜色改变成另一个颜色,例如红色改成黑色。但是很多时候用到的运算是旋转:

Left Rotation on Node P

Right Rotation on Node P
如上是以节点 P 为中心进行旋转运算。基本上维持红黑树的演算过程都是由变色与旋转依次组成。总结来说,红黑树的新增与删除操作是先透过一般二元树的新增与删除操作后,再从递补的节点开始向上进行红黑树性质维护。接下来,直接用例子演示走过一遍新增与删除节点的算法更能了解到变色与旋转的作用为何:
新增 (Insertion)
在新增操作上,新插入的节点一律都为红色,目的是希望红黑树维持规则 5 的约束,但也可能会违反除了规则 5 以外的其他规则,所以作完二元树新增节点的操作后,需要以新增的节点开始向上检查红黑树是否符合各项规则,修正红黑树的算法可能会有以下几种情境,因应不同情境会采取不同的修正过程:
情境一:红黑树为空,插入红节点后成为根结点,会违反规则 2,需将该节点改为黑色,即可完成红黑树维护。

Case 1: Red Node on the Empty RB Tree
情境二:在黑节点上与红节点 z 相接,不违反任何规则,无须作其他调整。

Case 2: Red Node on a Black Node
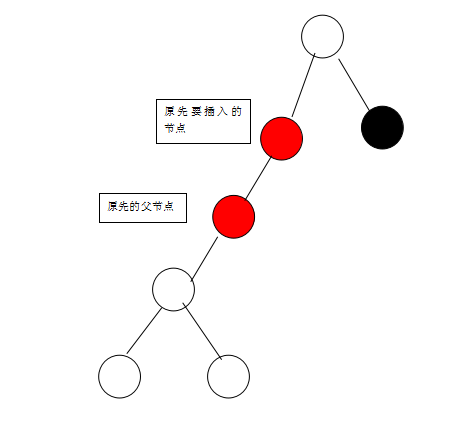
情境三:在红节点上与红节点 z 相接,会违反规则 4。从自己开始维护,若叔叔节点为红色,则先将父节点涂黑,用以保持规则 4,但这时会违反规则 5,所以须再将祖节点与叔节点分别涂成红色和黑色。接着再从祖节点继续往上检查维护。
如图片,可以看到最后的结果违反规则 4,该情境符合情境四所示,其父节点与自身皆为红色,所以下一轮会再以对应的流程处理。

Case 3: Red Node on a Red Node with its Red Uncle Node
情境四:在红节点上与红节点 z 相接,会违反规则 4。从自己开始维护,若叔叔节点为黑色且自己位置在父节点右边的状况,则先以父节点进行左旋,形成情境五,再作为情况五进行下一轮的处理。

Case 4: Red Node on the Right Side of Red Node with its Black Uncle Node
情境五:在红节点上与红节点 z 相接,会违反规则 4。从自己开始维护,若叔叔节点为黑色且自己位置在父节点左边的状况,则先将父节点改为黑色,用以保持规则 4,但这时会违反规则 5,所以须再将祖节点涂成红色,接着再以祖节点进行右旋,即能完成维护。(直觉上,节点 F 的左边路径会多一个黑色,可以透过右旋把黑色转掉)

Case 5: Red Node on the Left Side of Red Node with its Black Uncle Node
删除 (Deletion)
在删除操作上,删除一个节点时可能也会违反规则,所以作完二元树删除节点的操作后,视需要以递补节点开始向上检查红黑树是否符合各项规则,修正红黑树的算法可能会有以下几种情境,因应不同情境会采取不同的修正过程:
**情境一:**删除红节点,不违反任何规则,无须进行维护。

Case 1: Deletion on Red Node
情境二:删除节点为黑色需要进行维护。删除黑节点后,如果递补上来的节点为红色时,因为黑节点被删除会违反规则 5,所以直接将递补的红节点涂黑即可。或者,如果维护点在根结点时,如果根节点为红色,这时则违反规则 2,直接将根节点涂黑即可。

Case 2: Deletion on Black Node with Red Node Compensation
情境三:删除节点为黑色需要进行维护。删除黑节点后,如果递补上来的节点为黑色时,需要视情况补足路径上缺失的一个黑色,会以递补节点作为当前节点开始进行维护:
兄弟节点若是红色,则将兄弟节点涂黑、父节点涂红、再以父节点为基准左旋 (因为节点 C 的左边路径会少一个黑色,直觉会是透过左旋把黑色补起来)。但是可以发现现在的红黑树还是违反规则 5,虽然无法完全解决问题,但是递补节点的兄弟节点改变了,可以新情境再下一轮进行对应的修正。

Case 3: Deletion on Black Node with Black Node Compensation and Red Sibling Node
情境四:删除节点为黑色需要进行维护。删除黑节点后,如果递补上来的节点为黑色时,需要视情况补足路径上缺失的一个黑色,会以递补节点作为当前节点开始进行维护:
兄节点若是黑色,且兄节点之左节点与右节点同为黑色的时候,则将兄节点涂红。这时若父节点为红色则结束修正后将父节点涂黑即可,但是如果父节点为黑色,则需要再从父节点开始进行修正 (因为也要照顾到父节点的兄弟子树,看看是否也满足规则 5)。

Case 4: Deletion on Black Node with Black Node Compensation and Black Sibling Node with its Two Black Child Nodes
情境五:删除节点为黑色需要进行维护。删除黑节点后,如果递补上来的节点为黑色时,需要视情况补足路径上缺失的一个黑色,会以递补节点作为当前节点开始进行维护:
兄节点若是黑色,且兄节点之左节点为红色、右节点为黑色的时候,则将兄节点涂红、兄节点之左节点涂黑,再以兄节点为基准右旋,接着再进行下次的修正 (若采用左旋会变成相同情境,所以只好右旋,才可能跳离循环)。

Case 5: Deletion on Black Node with Black Node Compensation and Black Sibling Node with its Red Left Child Node
情境六:删除节点为黑色需要进行维护。删除黑节点后,如果递补上来的节点为黑色时,需要视情况补足路径上缺失的一个黑色,会以递补节点作为当前节点开始进行维护:
兄节点若是黑色,且兄节点之右节点为红色的时候,则将兄节点涂成与父节点相同的颜色、父节点涂黑、兄节点的右节点涂黑,再以父节点为基准左旋即可。(透过左旋与涂色操作将右边的黑色往左调整、并将右边红点涂黑补足缺失,希望符合规则 5 来让每条路径上黑色节点的数量一致)

Case 6: Deletion on Black Node with Black Node Compensation and Black Sibling Node with its Red Right Child Node
红黑树谨遵单单五条规则,前人总结了各种情况后,列出对应的处理方式。事后理解情境的对应处理方式虽然有迹可循,但是窥探其中奥秘却也令人慑服,很难想像这项算法从无到有所付出的庞大心力与挫折!
Reference
- Wikipedia Contributors, “Red–black tree,” January 23, 2020. [Online]. Available: https://en.wikipedia.org/wiki/Red%E2%80%93black_tree. [Accessed February 07, 2020].
- ITREAD01, “资料结构与算法:红黑树 (Red Black Tree),” January 06, 2019. [Online]. Available: https://www.itread01.com/content/1546725999.html. [Accessed February 07, 2019].
- Chiu CC, “Red Black Tree: Insert(新增资料)与Fixup(修正),” January 27, 2016. [Online]. Available: http://alrightchiu.github.io/SecondRound/red-black-tree-insertxin-zeng-zi-liao-yu-fixupxiu-zheng.html. [Accessed January 30, 2020].
- Chiu CC, “Red Black Tree: Delete(删除资料)与Fixup(修正),” January 30, 2016. [Online]. Available: http://alrightchiu.github.io/SecondRound/red-black-tree-deleteshan-chu-zi-liao-yu-fixupxiu-zheng.html. [Accessed January 30, 2020].
最容易懂得红黑树
Sun_TTTT 于 2017-03-23 17:00:58 发布
介绍
红黑树是一个平衡的二叉树,但不是一个完美的平衡二叉树。虽然我们希望一个所有查找都能在~lgN次比较内结束,但是这样在动态插入中保持树的完美平衡代价太高,所以,我们稍微放松逛一下限制,希望找到一个能在对数时间内完成查找的数据结构。这个时候,红黑树站了出来。
阅读以下需要了解普通二叉树的插入以及删除操作。
红黑树是在普通二叉树上,对没个节点添加一个颜色属性形成的,同时整个红黑二叉树需要同时满足一下五条性质
红黑树需要满足的五条性质:
性质一:节点是红色或者是黑色;
在树里面的节点不是红色的就是黑色的,没有其他颜色,要不怎么叫红黑树呢,是吧。
性质二:根节点是黑色;
根节点总是黑色的,它不能为红。
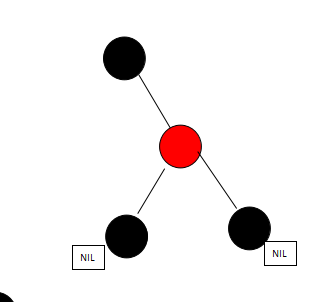
性质三:每个叶节点(NIL或空节点)是黑色;
这个可能有点理解困难,可以看图:
这个图片就是一个红黑树,NIL节点是个空节点,并且是黑色的。
性质四:每个红色节点的两个子节点都是黑色的(也就是说不存在两个连续的红色节点);
就是连续的两个节点不能是连续的红色,连续的两个节点的意思就是父节点与子节点不能是连续的红色。
性质五:从任一节点到其没个叶节点的所有路径都包含相同数目的黑色节点;
还是看图:
从根节点到每一个NIL节点的路径中,都包含了相同数量的黑色节点。
这五条性质约束了红黑树,可以通过数学证明来证明,满足这五条性质的二叉树可以将查找删除维持在对数时间内。
当我们进行插入或者删除操作时所作的一切操作都是为了调整树使之符合这五条性质。
下面我们先介绍两个基本操作,旋转。
旋转的目的是将节点多的一支出让节点给另一个节点少的一支,旋转操作在插入和删除操作中经常会用到,所以要熟记。
下面是左旋和右旋
左旋:
右旋:
下面讲讲插入
我们先明确一下各节点的叫法
因为要满足红黑树的这五条性质,如果我们插入的是黑色节点,那就违反了性质五,需要进行大规模调整,如果我们插入的是红色节点,那就只有在要插入节点的父节点也是红色的时候违反性质四或者是当插入的节点是根节点时,违反性质二,所以,我们把要插入的节点的颜色变成红色。
下面是可能遇到的插入的几种状况:
1、当插入的节点是根节点时,直接涂黑即可;
2、当要插入的节点的父节点是黑色的时候。
这个时候插入一个红色的节点并没有对这五个性质产生破坏。所以直接插入不用在进行调整操作。
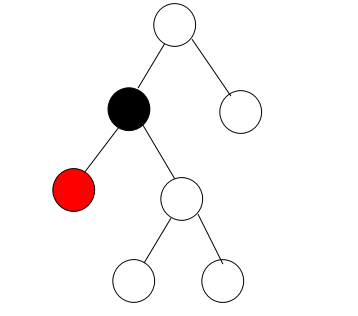
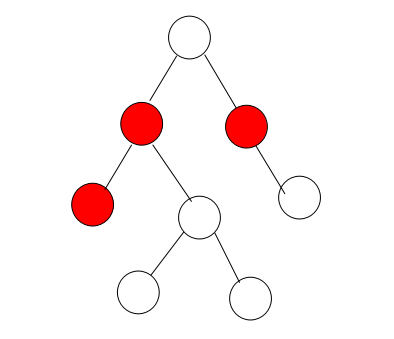
3、如果要插入的节点的父节点是红色且父节点是祖父节点的左支的时候。
这个要分两种情况,一种是叔叔节点为黑的情况,一种是叔叔节点为红的情况。
当叔叔为黑时,也分为两种情况,一种是要插入的节点是父节点的左支,另一种是要插入的节点是父亲的右支。
我们先看一下当要插入的节点是父节点的左支的情况:
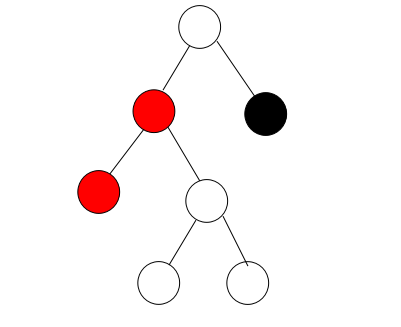
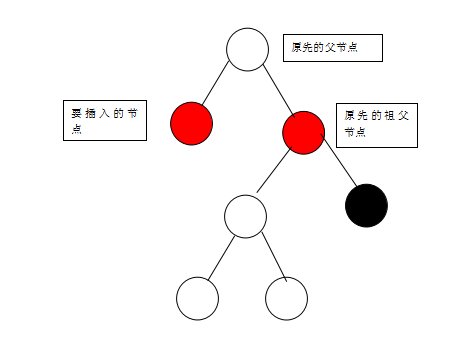
这个时候违反了性质四,我们就需要进行调整操作,使之符合性质四,我们可以通过对祖父节点进行右旋同时将祖父节点和父节点的颜色进行互换,这样就变成了:
经过这样的调整可以符合性质四并且不对其他性质产生破坏。
当插入的节点是父节点的右支的时候:
当要插入的节点是父节点的右支的时候,我们可以先对父节点进行左旋,变成如下:
如果我们把原先的父节点看做是新的要插入的节点,把原先要插入的节点看做是新的父节点,那就变成了当要插入的节点在父节点的左支的情况,对,是的,就是按照当要插入的节点在父节点的左支的情况进行旋转,旋转完之后变成如下:
4、如果要插入的节点的父节点是红色且父节点是祖父节点的右支的时候;
这个时候的情况跟情况3所表述的情况是一个镜像,将情况3的左和右互换一下就可以了。
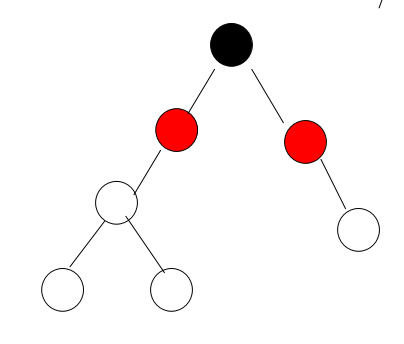
5、如果要插入的节点的父节点是红色并且叔叔节点也为红色,如下:
这个时候,只需将父亲节点和叔叔节点涂黑,将祖父节点涂红。
以上就是插入的全部过程。
下面我们再讲讲删除的操作:
首先你要了解普通二叉树的删除操作:
1.如果删除的是叶节点,可以直接删除;
2.如果被删除的元素有一个子节点,可以将子节点直接移到被删除元素的位置;
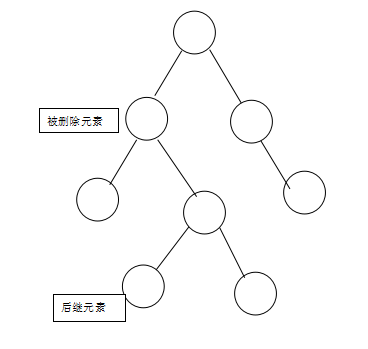
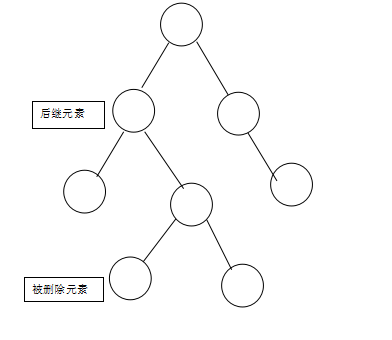
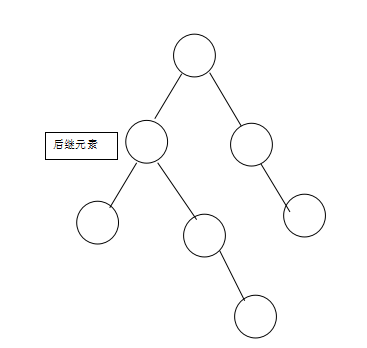
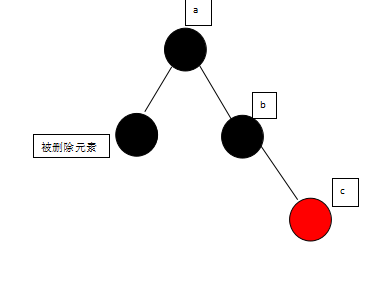
3.如果有两个子节点,这时候就可以把被删除元素的右支的最小节点(被删除元素右支的最左边的节点)和被删除元素互换,我们把被删除元素右支的最左边的节点称之为后继节点(后继元素),然后在根据情况1或者情况2进行操作。如图:
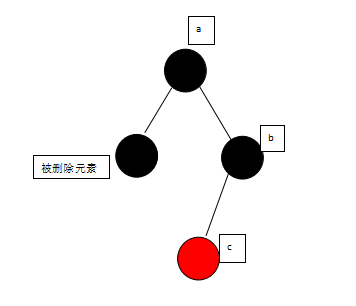
将被删除元素与其右支的最小元素互换,变成如下图所示:
然后再将被删除元素删除:
我们下面所称的被删除元素,皆是指已经互换之后的被删除元素。
加入颜色之后,被删除元素和后继元素互换只是值得互换,并不互换颜色,这个要注意。
下面开始讲一下红黑树删除的规则:
1.当被删除元素为红时,对五条性质没有什么影响,直接删除。
2.当被删除元素为黑且为根节点时,直接删除。
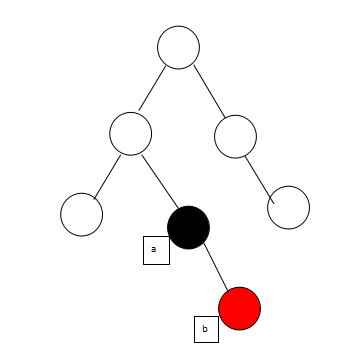
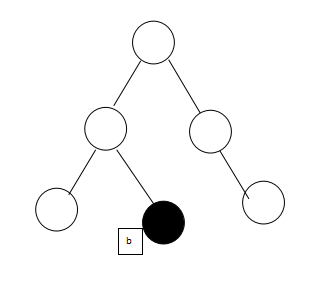
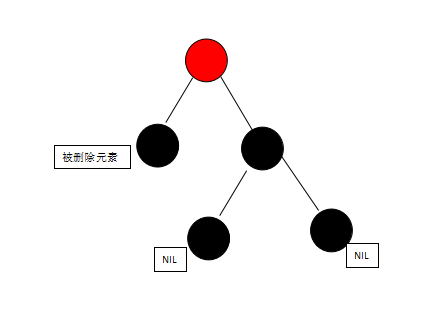
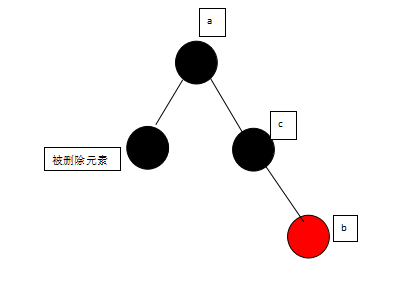
3.当被删除元素为黑,且有一个右子节点为红时,将右子节点涂黑放到被删除元素的位置,如图:
由
变成
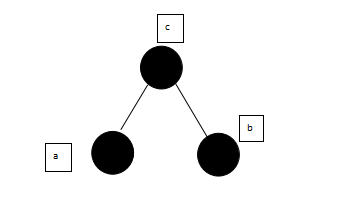
4.当被删除元素为黑,且兄弟节点为黑,兄弟节点两个孩子也为黑,父节点为红,此时,交换兄弟节点与父节点的颜色;NIL元素是指每个叶节点都有两个空的,颜色为黑的NIL元素,需要他的时候就可以把它看成两个黑元素,不需要的时候可以忽视他。
如图:
由
变成:
5.当被删除元素为黑、并且为父节点的左支,且兄弟颜色为黑,兄弟的右支为红色,这个时候需要交换兄弟与父亲的颜色,并把父亲涂黑、兄弟的右支涂黑,并以父节点为中心左转。如图:
由
变成:
6.当被删除元素为黑、并且为父节点的左支,且兄弟颜色为黑,兄弟的左支为红色,这个时候需要先把兄弟与兄弟的左子节点颜色互换,进行右转,然后就变成了规则5一样了,在按照规则5进行旋转。如图:
由
先兄弟与兄弟的左子节点颜色互换,进行右转,变成:
然后在按照规则5进行旋转,变成:
7.当被删除元素为黑且为父元素的右支时,跟情况5.情况6 互为镜像。
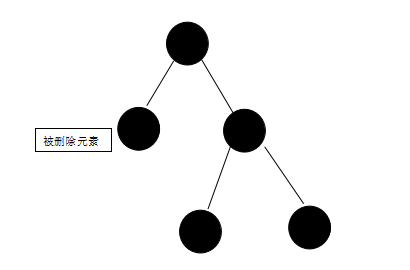
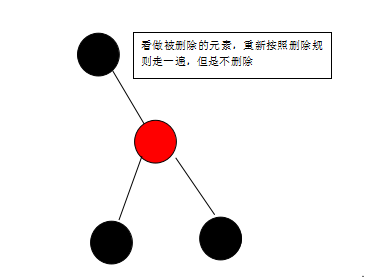
8.被删除元素为黑且兄弟节点为黑,兄弟节点的孩子为黑,父亲为黑,这个时候需要将兄弟节点变为红,再把父亲看做那个被删除的元素(只是看做,实际上不删除),看看父亲符和哪一条删除规则,进行处理变化如图:
由:
变成:
8.当被删除的元素为黑,且为父元素的左支,兄弟节点为红色的时候,需要交换兄弟节点与父亲结点的颜色,以父亲结点进行左旋,就变成了情况4,在按照情况四进行操作即可,变化如下:
由:
交换兄弟节点与父亲结点的颜色,以父亲结点进行左旋 变成:
在按照情况四进行操作,变成:
好了,删除的步骤也讲完,没有讲到的一点就是,在添加删除的时候,时刻要记得更改根元素的颜色为黑。
这里并没有语言实现,只是讲了一下红黑树的插入删除步骤,你可以根据步骤自己把红黑树实现。
[点击这里]- 数据结构之红黑树插入与删除全程演示 梦醒潇湘 love 2013-01-23 11:15:08
http://blog.chinaunix.net/uid-26548237-id-3480169.html
已附本文后,照着规则一步一步的构建一个红黑树吧。
最后:
-
红黑树的实现其实是一个 2、3、4 树,只是将双节点或者三节点用红色进行了标示,如果你将红色节点放到和它父元素相同的高度,并把它和父元素看做是一个元素,你就会发现,变成了一个高度为 lgN 的二叉树,这个 2.3.4 树对红黑树很有启发意义。
-
上面的步骤其实可以不用死记硬背,是可以推导出来的,因为我们是把一个平衡但通过插入或者删除破坏了平衡的红黑树再次平衡,同过旋转让位,改变红黑颜色,使之符合那五条基本性质。比如遇到删除操作情况四的时候,我们可以把那个删除元素去除,发现左边比右边少一个黑元素,这个时候,怎么办,我们发现兄弟节点的子元素有一个红元素,操作这个不会影响那五条性质,所以我们通过变换颜色,旋转,即可让左右两边的的黑色数目一样。
-
旋转操作的目的是出让一个元素到另外的地方并且符合二叉树左小右大的性质,交换颜色的目的是为了保持红黑树的那五条性质。
-
要时刻记得 ,一切的操作都是为了保持那五条性质。
最后的最后,其实还有一种更为简单的红黑二叉树,这个简单的红黑二叉树实际上是一个 2.3 树,他只允许左节点为红节点,但是性能上肯定是不如这个红黑树。这个简单的红黑二叉树在《算法》第四版有介绍,掌握完之后再看这个简单的红黑二叉树,就会觉着简单 easy。
最后的最后的最后,一定要尝试着自己推导一下插入删除规则啊,不然经常忘,是睡一觉起来再看就有点懵逼的那种忘。
红黑树介绍
RWCC于 2022-05-28 10:30:00 发布
红黑树目录
-
红黑树的概念
-
红黑树的性质
-
红黑树节点的定义
-
红黑树结构
-
红黑树的插入操作
-
红黑树的验证
-
红黑树与 AVL 树的比较
红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red 或 Black。 通过任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。

红黑树的性质
-
每个结点不是红色就是黑色
-
根节点是黑色的
-
如果一个节点是红色的,则它的两个孩子结点是黑色的
-
对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
-
每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
思考:为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?

我们分析一下:
最短路径为全黑,最长路径就是红黑节点交替(因为红色节点不能连续),每条路径的黑色节点相同,则最长路径、刚好是最短路径的两倍。
红黑树节点的定义
// 节点的颜色
enum Color{
RED, BLACK};
// 红黑树节点的定义
template<class ValueType>
struct RBTreeNode
{
RBTreeNode(const ValueType& data = ValueType(),Color color = RED)
: _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
, _data(data), _color(color)
{
}
RBTreeNode<ValueType>* _pLeft; // 节点的左孩子
RBTreeNode<ValueType>* _pRight; // 节点的右孩子
RBTreeNode<ValueType>* _pParent; // 节点的双亲(红黑树需要旋转,为了实现简单给出该字段)
ValueType _data; // 节点的值域
Color _color; // 节点的颜色
};
思考:在节点的定义中,为什么要将节点的默认颜色给成红色的?
插入红色节点树的性质可能不会改变,而插入黑色节点每次都会违反性质4.
通过性质发现: 将节点设置为红色在插入时对红黑树造成的影响是小的,而黑色是最大的
总结:将红黑树的节点默认颜色设置为红色,是为尽可能减少在插入新节点对红黑树造成的影响。
红黑树结构
为了后续实现关联式容器简单,红黑树的实现中增加一个头结点,因为根节点必须为黑色,为了与根节点进行区分,将头结点给成黑色,并且让头结点的 pParent 域指向红黑树的根节点,pLeft域指向红黑树中最小的节点,_pRight域指向红黑树中最大的节点,如下:










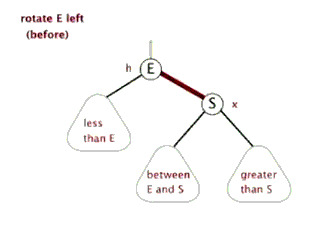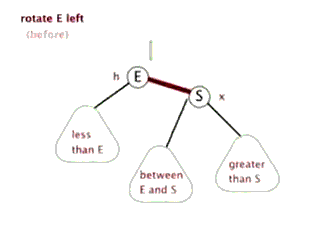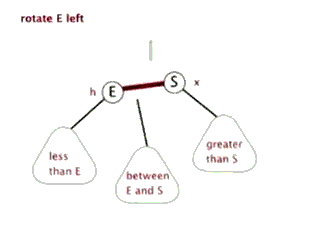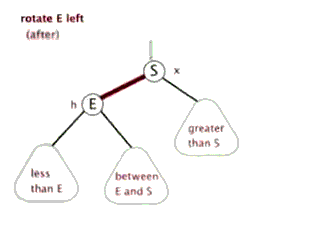
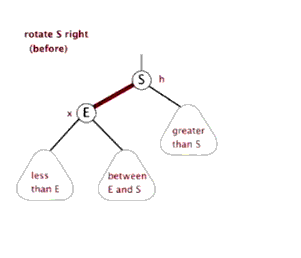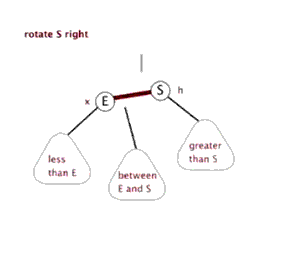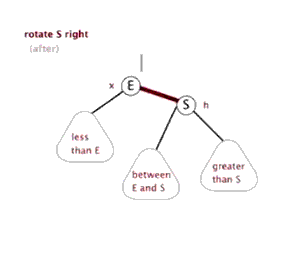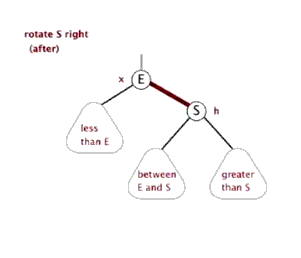


 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1701
1701

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








