自指 | Self-reference

注：本文为 “自指” 相关文章合辑。

未整理去重。
如有内容异常，请看原文。

---

自指丨自指是什么？

原创 自指 2023 年 11 月 22 日 16:16 山东

《自指》

自指是指系统或理论可以描述或操作自身的能力。它涉及到一个系统可以引用、操纵或分析自己的特征、结构或行为的特性。

在数学和计算机科学中，自指经常出现在逻辑、集合论和编程语言中。例如，哥德尔不完备定理中的重要思想就是关于形式化系统如何通过引入自指来推导出它无法证明的陈述。同时，在计算机科学中，递归函数和自引用数据结构都涉及到自指的概念。

在哲学和认知科学领域，自指也被广泛讨论。自指被认为是思维及意识的一种基本属性。自指与反馈机制相互关联，反馈是一个系统从输出信号中获得输入信号的信息，而自指就是在系统的输出中包含了对自身状态的信息。

自指还与复杂性理论和系统科学相关。自指系统常常显示出非线性动力学和混沌行为。这些系统可以通过反馈机制、自组织和自适应性等特性来适应环境并产生复杂的行为模式。

总而言之，自指是指系统或理论具有引用、操纵或分析自身的能力。它在数学、计算机科学、哲学和认知科学领域有着重要的应用和意义。

— END —

---

研究自指的最好方法是自指本身

原创 刘逸川 智能探索 2024 年 08 月 18 日 22:47 上海

自指即自我指涉，典型的例子是 “这句话是假话”，自己蕴含了自己。虽然这似乎是一种特殊的存在，但是其实如果将其普遍化，则可以解释很多现象，而且这种解释会比已有的解释更加简洁，更加接近事物的本质。自指被很多人认为是理解宇宙的关键，目前通用人工智能没有取得突破性进展可能和自指的研究没有突破有关。

自指的研究之所以没有突破，一个很大的原因是研究者没有找到研究自指的最好方法。目前大多数研究和研究者自身是分离的。例如研究人工智能，那么研究者会在研究时研究，生活时生活。虽然二者有时存在交集，而且存在互相影响，但是这是相对微弱的存在。这看起来也很正常，也的确很难将二者融为一体。然而，研究自指不同，虽然也可以分离研究，但是这样没有领悟到自指的精髓，很难取得成功。自指相对于人工智能、数学、物理等学科，本身就是一种特殊的存在，就像 “这句话是假话” 相对于大多数语句是一种特殊的存在一样，因此应该用一种特殊的方法研究。这种方法非常有趣的是自指自身，也就是需要将研究者自身和研究融为一体，进入某种沉浸其中的状态。

当然，也不是完全地投入其中，因为自指的本质其实是对立统一，既要分离又要有回归。就像 “这句话是假话”，在于 “这句话” 从句子中分离出来，需要去看看它代表的是什么，结果发现回到了这句话本身，因此创造了自指。

如果有更多研究者摆脱传统的研究方法，用自指去研究自指，相信会取得不少的进展。

---

什么是自指

集智百科 集智俱乐部 2025 年 02 月 12 日 19:03 上海

在自然语言或形式语言 formal language 中，当一个句子、想法或公式指向自己时，就会出现自指现象 Self-reference。（自指的英文 Self-reference 中，reference 有 “参照” 的意思。）参照可以直接通过一些中间句或公式来表达，也可以通过一些编码来表达。在哲学中，它也指一个主体谈论或指称自己的能力，也就是说，具有第一人称主格单数代词 “我” 在英语中所表达的那种思想。

古代的符号衔尾蛇，一条吞噬自己尾巴的蛇，表示自指

自指 Self-reference 经常在数学、哲学、计算机编程和语言学中被研究和应用。自指陈述有时是自相矛盾的，也可以被认为是递归的。

自指在逻辑、数学和计算中的体现

在古典哲学中， 悖论 Paradoxes 是由自指概念创造出来的，比如全能悖论 omnipotence paradox （上帝悖论） ：是否有一个上帝或者全能的存在，可以创造出一个他自己也举不起的石块？

还有埃庇米尼得斯悖论 Epimenides paradox，又称说谎者悖论。这一悖论有许多不同的表述形式，古希腊克里特岛人说的 “所有克里特岛人都是骗子” 是有记载的最早版本之一。当代哲学有时使用同样的技巧来证明一个假定的概念是没有意义的或者定义不明确的。

在数学和可计算性理论中，自指(也被称为 “不确定性”) 是证明许多系统局限性的关键概念。哥德尔定理 Gödel’s theorem 用它来表明，没有一个形式上一致的数学系统可以包含所有可能的数学真理，因为它不能证明某些关于它自身结构的真理。在计算理论中，哥德尔定理的等价表述是停机问题，这一问题表明计算机不能完成关于自身的推理。这些证明关系到数学悖论的悠久传统，如罗素悖论和贝瑞悖论，并最终关系到经典哲学悖论。

在博弈论 game theory 中，当博弈双方必须模拟对方的心理状态和行为时，就会出现不确定的行为，导致无穷递归。

在计算机程序设计中，自指发生在反射 reflection 中，程序可以像读取或修改其他数据一样读取或修改自己的指令。许多编程语言在某种程度上支持反射，具有不同程度的表达能力。此外，在函数式编程中的递归(与数学递归关系式相关) 中可以看到自引用，其中代码结构在计算过程中反向引用自身 。把自指从潜在的矛盾概念 “驯服” 到良好的行为递归一直是计算机科学的伟大成功之一，现在经常被 “元语言” 机器学习用于编写编译器。使用编译器编译其自身被称为 bootstrapping。无论是使用汇编语言还是使用 Lisp 之类的函数式语言，编写让程序可以进行自修改的程序都是可能的，但在实际编程中通常不提倡这样做。计算器硬件使用了触发器中的自指，触发器是数字存储器的基本单位， 它随时间推移扩展条件，存储潜在的逻辑自相关矛盾。自指思维在程序员文化中普遍存在，许多程序和首字母缩略词都是以自指的方式命名，这是一种幽默的形式，比如 GNU(“ GNU 不是 Unix”) 和 PINE(“ PINE 不是 Elm”)。GNU Hurd 是以一对相互自我指涉的缩写命名的。

Tupper 自指公式的 Wolfram 实现，图像与公式本身一致

Tupper 自指公式是一种数学上的奇思妙想， 它的图像与其公式本身的样子几乎是一样的。

一种自复制的计算机程序 —— 蒯恩 Quine

在计算机科学中，蒯恩 Quine 是一种自复制的计算机程序，也代表了自指的含义。当计算机执行这个程序时，程序会输出自身的代码。例如，利用 Python 语言编写的一个 Quine 程序如下如下：

a='a=%r;print(a%%a)';print(a%a)

将以上代码写入文件，然后执行，会发现程序的输出就是程序代码自身：

在生物学中

自指在生物学中表现为自复制 self-replication，正如 DNA 和 RNA 复制机制所体现的那样。康威的生命游戏中有自复制的模型，这些模型启发制造工程系统，比如自复制的 3D 打印机 RepRap 就是一个很好的例子。

在艺术中

自指在文学与电影中同样存在，譬如，一个作者可能在作品本身的背景下提到他自己的作品。

例子包括米格尔・德・塞万提斯 Miguel de Cervantes 的《堂吉诃德》，莎士比亚 Shakespeare 的《仲夏夜之梦》，《暴风雨》和《第十二夜》，丹尼斯・狄德罗 Denis Diderot 的《宿命论者雅克和他的主人》 ，意大利卡尔维诺 Italo Calvino 的《如果在冬夜，一个旅人》，尼古拉・戈戈 Nikolai Gogol 的许多故事，约翰・巴特 John Barth 的《游乐园里的迷失》 ，路伊吉・皮兰德娄 Luigi Pirandello 的《寻找作家的六个人物》 ，费德里柯・费里尼 Federico Fellini 的 《八部半》和 布莱恩・福布斯 Bryan Forbes 的《陋室红颜》。

推理小说作家塞谬尔・迪兰尼 Samuel R. Delany 在他的小说《新星》和《代尔格林》中使用了这一点。在前者中，卡廷 Katin(一个航天小说家) 担心一个长期存在的诅咒，即小说家会在完成任何给定的作品之前死去。Nova 在中间去世，因此增加了诅咒的可信度，并使读者意识到 小说家是故事的作者；同样地，在《代尔格林》一书中 ，德拉尼有一个名为 Kid(或 Kidd，在某些部分) 的主角，这个主角的生活就是小说本身的镜像 。在科幻恶搞电影《太空炮弹》中，导演梅尔・布鲁克斯 Mel Brooks 拍摄了一个场景，反派们 正在观看自己故事的 VHS 拷贝，这个场景展示了他们无限地观看自己的 “观看自己”。也许最早的例子是在伊利亚特 Homer’s Iliad，特洛伊的海伦哀叹道: “为了尚未出生的后代 / 我们将生活在歌曲中”(出现在歌曲中)。

艺术中的自指与打破第四道墙和元引用 meta-reference 的概念密切相关。豪尔赫・路易斯・博尔赫斯 Jorge Luis Borges 的短篇小说在许多方面玩弄着自指和相关的悖论。塞缪尔・贝克特 Samuel Beckett 的话剧《克拉普的最后碟带》完全由主人公自己听录音组成，大部分是关于其他录音的。在 20 世纪 90 年代和 21 世纪初，电影自指是虚幻电影 Rubber Reality 运动的一个流行部分，特别是在查理・考夫曼 Charlie Kaufman 的电影《成为约翰马尔科维奇》和改编作品中，后者可以说是把这一概念推动到了鼎盛时期，因为它试图在一个德罗斯特效应剧本化的版本里描绘自己的创作。

各种创世神话援引自指来解决是什么创造了创造者的问题。例如，埃及创世神话中有一个神吞下自己的精液来创造自己。衔尾蛇是一种神话中的会吃自己的龙。

《古兰经》Quran 中有许多自指的例子。

超现实主义画家勒内・马格利特 René Magritte 以自指类的作品著称。他的画作《形象的背叛》The Treachery of Images，图片是一个烟斗，但是却包含了 “这不是烟斗” 的字样，其真实性完全取决于单词 ceci(英语中的 “ this”) 是指画作所描绘的烟斗，还是指画作本身，抑或 “ceci” 这个单词，或者是指这个句子本身。

埃舍尔 M.C. Escher 的艺术也包含了许多自指的概念，比如他的版画作品《画廊》（Print Gallery）。埃舍尔的艺术所作的最后研究包括了其艺术与信息科学、人工智能的关系，这在先前的研究中被忽略了，但是这一点的重要性被侯世达细心的发现了，并写在他赢得 1980 普利策奖的《Gödel，Escher，Bach：一条永恒的金带》一书中。

在语言学中

一个描述自己的词叫做自体词(或自动词)。这通常适用于形容词，例如英文中 “多音节” 一词 sesquipedalian(即 “ sesquipedalian” 是一个多音节的的单词) ，但也可以用于其他词类，如 TLA，作为 “三个字母缩写” 的三个字母的缩写。

A sentence which inventories its own letters and punctuation marks is
called an autogram.

一个有自己的字母和句读的句子叫做自拍像 autogram。

元语句中的句子内容与宾语中的句子内容相同是元语句的一种特殊情况。这样的句子指的是它自己。然而，这种类型的元语句也可能导致悖论。“这是一个句子。” 可以认为是一个自指的元语句，这显然是正确的。然而，“这句话是假的” 是一个元句子，它导致了一个自指悖论。这样的句子可能会导致问题，例如，在法律中， 元语句使法条的陈述可能会相互矛盾或自相矛盾。库尔特・哥德尔 Kurt Gödel 在他的公民身份仪式上宣称，他在美国宪法中发现了这样一个悖论。

自指偶尔会在传媒中出现，比如媒体报道自己的时候，例如 BBC 报道 BBC 公司裁员的事件，著名的百科全书维基百科可能被要求提供关于维基百科上的文章。

Fumble rules 是一系列好的语法和写作规则，描述这些规则的句子本身违反了这些规则 ，也是一种自指的规则，比如 “避免像瘟疫一样的陈词滥调” 和 “不要使用没有双重否定”。这个术语是威廉・萨菲尔 William Safire 在一份她发表的规则列表中创造出来的。

在流行文化中

侯世达的书，特别是 “Metamagical Themas” 和 “《GEB》” 使用了许多自指概念，这些书籍在 20 世纪 80 年代成功地将 “自指” 概念引入主流知识文化。Hofstadter 定律，做一件事情所用的时间总是比你预期的要长，即使你考虑到了候世达定律。[10] 是一个自指格言的例子。 候世达 Hofstadter 还提出了 “Reviews of this book” 的概念， 即一本 “只包含对自己的评论” 的书，这本书已经使用 wiki 和其他技术实现。候世达的 “怪圈” 试图将意识映射到自指上，但这在心灵哲学中是少数人的立场。

“递归科幻” 或元小说的子类型现在非常流行，以至于在新英格兰科幻小说协会 New England Science Fiction Association 的网站上孕育了一个粉丝维护的书目；其中一些有关于科幻电影，一些有关于科幻小说及其作者的文章。

摄像 - 屏幕自指模拟

摄像机对着电视机照，再把摄得的图像反传给电视会得到什么？答案似乎应该是什么都没有。集智俱乐部的张江等人通过组织相关的实验，证实这样的一个自指系统能给我们带来非常丰富的复杂图案，一些奇妙的结构会从电视屏幕中源源不断的飞出来。当他们略微调节电视机的亮度、颜色以及摄像机的焦距等等参数以后，却得到了比书中描述的现象更加丰富的图案。而且运用不同的摄像机转动不同的角度会得到完全不一样的结果。

并且，他们经过长期的探索，开发了相应的计算机模拟程序。找到了一种能够近似模拟电视机中动态图像的计算机仿真办法。这就是下面的 Java 仿真程序。

源代码：
https://wiki.swarma.org/index.php?title=文件:Selfref.zip

关于更多的详细流程操作和过程记录可查词条：摄像 - 屏幕自指模拟
https://wiki.swarma.org/index.php?title=摄像-屏幕自指模拟

下面是一些仿真软件做出来的结果（静态图片）：

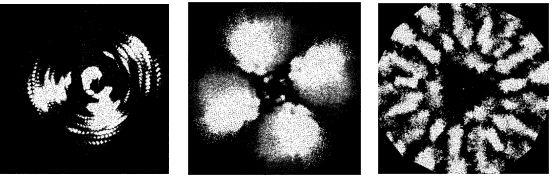
说明

本词条由集智俱乐部众包生产，难免存在纰漏和问题，欢迎大家留言反馈或者前往对应的百科词条页面进行修改，一经修改，可以获得对应的积分奖励噢！

---

自指机器的奥秘

原创 东方和尚 集智俱乐部 2018 年 02 月 10 日 11:33

众里寻她千百度，那人却在灯火阑珊处。我们耗资了数千亿美元、花费了将近百年的时间去寻求构建智能机器的奥秘，却不知它早已存在于数理逻辑、计算机科学之中，这个奥秘就是自指（Self-reference）。 早在 20 世纪初计算机科学诞生的年代，罗素（Russell）、哥德尔（Godel）、图灵（Turing）、克林尼（Kleene）、蒯恩（美国哲学家，Quine）等人就已经将大量自指的技巧引入了数学和基础逻辑之中，证明了一大批定理。然而，冯・诺伊曼的敏锐洞察力却超越了所有这些人。他不仅指出现实的生命之所以可以自繁殖就是因为它是一台自指的机器，他甚至还指出是自指＋热力学创造达尔文式生物进化的原始动力。因此，冯・诺伊曼所说的复杂度阈值就是这个自指，一个系统实现了自指，它就可能在自指动力学指引下不断钻概率论中的漏洞，完成自我复制、进化和升级；而如果没有实现自指，则它就必然会在热力学作用下逐渐降级、退化。如何实现一台自演化的自指机器？也许这将是引发下一场 AI 革命的核心问题。

自指机器的奥秘

在翻译过程中，做了以下的添加和修改：

1、为了方便阅读，为原文进行了分段，并加上了段标题；

2、为了让读者感觉更亲切，加上了若干副插图。

3、为原文添加了大量的评论，东方和尚的评论和张江老师的评论都会标注出来，另外，因为这本书是冯・诺依曼的助手 Arthur W. Burks（遗传算法之父 John Holland 的博士生导师），所以在框中的文字是编者加的注解。大家要注意分辨。

自动机的构建

Arthur W. Burks：

冯·诺伊曼只是简单地提了一下他打算使用的原件的种类。这些零件与 McCulloch - Pitts 的神经模型很像。有些零件是 “除了在两端之间建立刚性的几何连接以外没有任何功能的”；另一种零件被称为 “运动组件”，起到 “类似肌肉的作用”，这种零件在受到刺激时长度会收缩为零；还有一种零件遇到脉冲就 “建立或者断开一个连接”；他说至多只需要十几种这样的零件就足够了。由这些零件所组成的自动机能够自动地捕捉偶然撞上来的零件：“我们可以发明一种装置” 使它能够识别出捉住的零件类型。

在 1948 年 6 月，可能是为了准备 9 月份的希克森会议，冯·诺伊曼在普林斯顿的高等研究院（IAS）给他的一些朋友讲了三堂有关自动机的课。据我所知，这几堂课包括了冯·诺伊曼对于自复制自动机的最详细的分析。因此，编者做了一番努力，尽量从听课的笔记和与会者的记忆中拼凑出关于零件以及它们的功能的细节，兹叙述如下：

冯·诺伊曼描述了八种不同的零件，并用直线来代表它们，且标出了位于中间或者两头的输入和输出端子。自动机在离散的时间下运行，每个零件都要用一个单位的时间做出反应。我们不知道由八种零件构成的这个列表是否完成了冯·诺伊曼的意图，但编者猜想，就此问题，他还没有最后得出结论。

有四种零件是用于处理逻辑和信息的：

• 应激零件（Stimulus organ）：用于接收和发出刺激信号，并且接收这些信号是相分离的，该零件的真值函数相当于 “p 或 q”。
• 合并零件（Coincidence organ）：实现 “p 与 q” 这个布尔函数。
• 抑制零件（inhibitory organ）：实现 “p 与 非 q” 布尔函数。
• 激发信号产生器（stimuli producer）：起到刺激信号源的功能。

第五种零件是 刚体零件（rigid member），这是一种刚性的组件，被用来当作自动机实体的结构骨架。刚体零件不接收任何刺激，它对于信号是绝缘的。刚体零件可以同其它的刚体零件组合起来，也可以用来架设其他的零件。

另有一种 连接零件（fusing organ），当它受到刺激的时候会把两个零件 “焊接” 在一起。编者认为连接零件的工作方式如下，假设一个结构上的 A 点将要和另一个结构上的 B 点焊接在一起，这时候连接零件上面活动的输出端子就会同时与 A 和 B 接触，在 t 时刻向连接零件发送一个刺激信号，于是导致 t + 1 时刻 A 和 B 两点就会被焊接在一起。然后连接零件就可以离开现场。

此外还有 切割零件（cutting organ），受到刺激的时候，切割零件就会把连接切开。

第八种零件称为 肌肉零件（muscle），可以用来产生运动。肌肉零件一般是刚性的，可以连接到其它的零件之上。如果在 t 时刻肌肉零件受到刺激，在 t + 1 时刻它就会收缩到零长度，并保持之上的所有连接。只要刺激信号不消失，肌肉零件就一直保持收缩。编者认为肌肉零件这样工作：比如肌肉零件 1 把一个结构上的 A 点和另一个结构上的 B 点连在一块，肌肉零件 2 又把 A 点和一个连接零件的输出端子 C 连在一起。然后一旦肌肉 1 和 2 都受激发，它们就会收缩，从而把 A、B、C 三点凑在一起，这时候激发连接零件，A 和 B 点就会被焊接起来。最后，当肌肉上的刺激消失之后，它们就会恢复到原有的长度，肌肉１上至少有一个端子也会同 A、B 点分开。至于一开始肌肉和其他零件的连接是怎样实现的，后来又是怎样断开的问题，冯·诺伊曼似乎没有提到。

漂浮着机器零件的池塘（译者加）

摘自 Gene Pool 人工生命软件

按照冯・诺伊曼的设想，自动机按照以下的方式制造其它的自动机：在一个平面上漂着母自动机，周围是无穷无尽的零件海。母自动机在存储器中包含有将要制造的子自动机的描述。并按照描述，捡起所需的零件装到正确的位置上去。要做到这点，母自动机必得包含一个能够抓住并且辨认零件的装置。在 1948 年 6 月的课上，冯・诺伊曼对这个问题只是稍微提了几句话：两个激发零件从母自动机上像触角一样伸出来，当它们碰到其它零件的时候，就可以通过激发一个信号去测试所遇零件的性质，如激发零件能够传送信号，而结构零件就不能；肌肉零件受到刺激则会收缩等等。

冯・诺伊曼在他首次的设计尝试中，忽略了能源和能量的问题。他打算之后再考虑这个问题，比如把电池作为一种新的基本零件引入进来。除此以外，冯・诺伊曼的这个早期自复制模型处理了以下的几何动力学问题：包括运动、接触、定位、连接、切断；但是没有考虑真正机械和化学意义上的能量和力的问题。因此把这个模型叫做自复制的动力学模型（kinetic model）；本书的第二部分介绍的是冯・诺伊曼之后提出的自复制元胞模型（cellular model），读者可以对比此两者。

在 1948 年 6 月的课上，冯・诺伊曼提出了动力学自复制模型是否需要三维空间才能实现的问题。他怀疑只有在三维空间或者黎曼曲面（多连接的复数平面）上才能实现该模型。但在本书的第二部分中，二维平面已经足以实现自复制的元胞模型了。这似乎说明，二维平面也足以实现动力学自复制了。

让我们继续回到伊利诺斯的讲座中：冯・诺伊曼讨论了自复制自动机的一般设计方法。他说，在理论上只要有足够的时间和原材料，就可以建立一个能够复制任何机器的车间。这个车间中有一台具备如下能力的机器 B：对于任何一个结构或者机器 X，则机器 B 会自动扫描 X，并把 X 上面的所有零件，以及这些零件的相互连接方式都列成表格，从而得到 X 的完全描述。再根据以上的描述，机器 B 就可以把 X 同样地复制出来。“这同自复制已经非常接近了，因为我们可以把 B 喂给它自己从而得到自己的一个复制品”

但是，相对说来比较简单的，而且同样可以实现最终目的的做法是，不去直接建立能够复制任何给定结构或者样本的自动机，而是去做一个能够根据逻辑描述来组装目标的自动机。因为，按照任何可设想的方式，复制一个对象都必定分成两步，先是从具体实物抽象出描述，然后再从这个描述到具体实物。因此，先做后面这步会比较简单一些。

要做到这件事，**我们必先得有一个自动机的公理化描述。**如我们所见，我的做法和图灵的通用自动机很像，都是从一个理想机器的通用描述开始。我之前比较含糊地提到过，我们一共有大约十几种基本零件，如果把它们的细节都具体写出来的话（估计两页纸就够了），我们就可以得到一套刻画自动机的无歧义的形式语言。现在，我们可以把这些形式记号转变为二进制，并记录在打孔纸带上面。因此，任何自动机的描述都可以记录在打孔纸带上。我们可以不描述对自动机每一个零件以及这些零件之间的连接方式；而是直接描述这个自动机是如何被一步一步组装出来的，后者会比较方便一些。

Arthur W. Burks：

冯・诺伊曼接下来说明了怎样把刚体零件转换成二进制的打孔纸带的过程。见下图，其中每一个基本链的交汇处都可以用一个二进制字符编码。1 表示对应位置有零件连接，0 表示没有。如果对这个数字串进行读写，那么对应位置上的零件也相应地被修改。

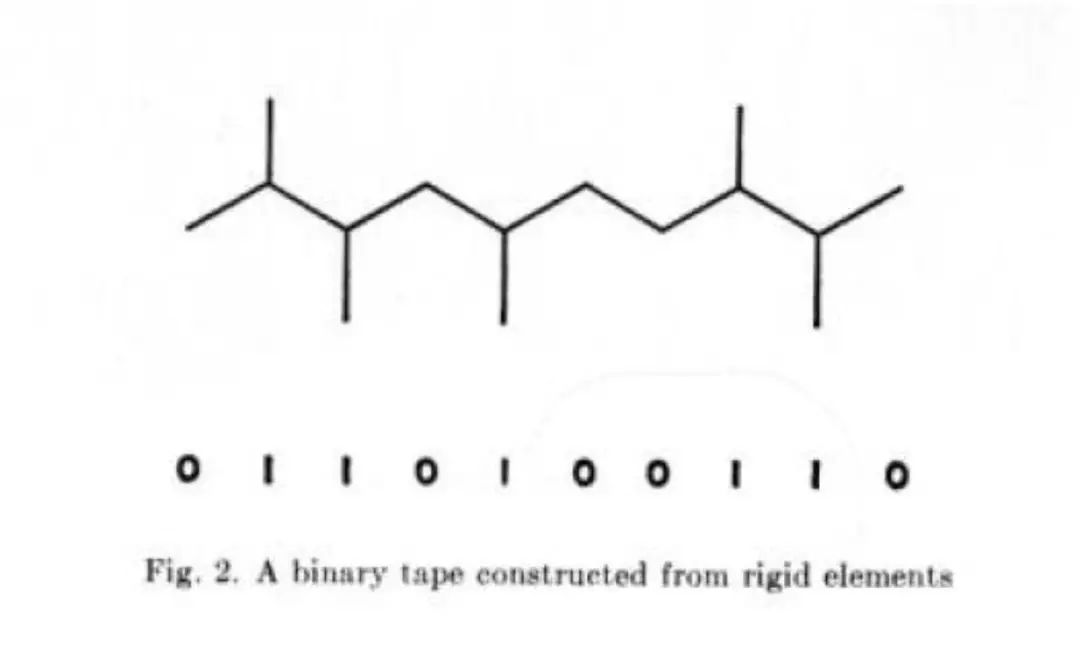
由于我有一种纯数学上的习惯，喜欢把一切东西用最简单的记号表示出来，所以这里的表示可能有些过于简化了。因为我现在用的是二进制表示，所以在上图中，我们不考虑支链的问题，或者说每个位置只能连接一个零件。现有的描述语言和符号系统所用的符号要比二进制更多，但是这里只要用二进制符号就足够了，我们可以毫无困难地表示出更多的符号，只需把支链也分别表示出来，并接上去就行了。其实，我们并不一定要用线性的符号系统。我们也可以用复杂得多的，包括循环的环状结构来表示自动机，但那个时候非线性的代码就不灵了。有理由怀疑我们对于看似简单的串行编码的偏好，只不过是一种来自语言的习惯；很可能存在着非串行的，效率却高很多的自动机描述方式，由于我们对于这类组合却缺乏直觉。

自复制自动机的核心

冯・诺伊曼自复制自动机模型的形象展示（译者加）

图片来源：http://informatics.indiana.edu/rocha/ss504_5.html

自动机自复制原理阐述

要给出一个完全的公理化描述体系并不太困难，由此我们可以把任何可设想的自动机用二进制代码表示出来。任何这样的描述都可以用类似上图的一串零件来代表。

假设自动机 $X$ 的符号串是 $\Phi (X)$。接下来，我们可以设计一台通用构造器（Universal constructer）$A$，当我们把 $\Phi (X)$ 喂给 $A$ 的时候，它就能够逐步地利用悬浮在周围的零件，把 $X$ 一点点的组合出来。实际设计工作当然是很麻烦的，但是理论上却是可以办到的。因为这个过程可以归纳为形式逻辑的分步推理，从性质上说，这和通用图灵机并无区别。

还有一件事要说，我之前提到过，要制造一台能够直接复制任何自动机的机器是比较复杂的。所以最好是从要复制的机器的描述而不是从机器的实体来进行复制。但是我想补充一点，存在着某复制机器可以直接拷贝线性的刚体零件链，这是很简单的。因为导致实体复制困难的真正原因是，实体自动机的结构同我们串行的思考习惯完全不同，各种各样的零件朝着各个方向相互连接。仅仅是把已经扫描过的零件排除在列表外，便是很麻烦的事情。但是拷贝一根长链并无这种困难。所以，我可以假设存在一台通用拷贝机器 $B$（copy automaton），当我们把任何描述输入 $B$ 的时候，$B$ 就会制造出同样的两份描述出来。

在完成以上两步之后，可能给人一种错觉，在此过程中复杂度衰退的原理似乎仍然没被打破。在表面上看，似乎在复制过程中，既没有产生更微妙的东西，也没有建立更多的联系。$A$ 只能按照描述来制造 $X$。而按照对于复杂度的一般认识，$X$ 的复杂度是和 $X$ 的描述相等的。另一方面，$B$ 拷贝得到了两份 $\Phi (X)$，但是两个同样的事物放在一起，没有理由说它们作为整体的复杂度要高于其中一个的复杂度，并且，我们还需要额外的机器 $B$ 来完成复制。但实际上并不是这样的。

现在我们可以做下面这件事，我们可以把机器 $A$ 和 $B$ 组合在一起，并给 $A+B$ 添加一个控制器 $C$。$C$ 按照下列方式对 $A$ 和 $B$ 施加控制：

1. $C$ 先命令 $B$ 拷贝两份描述 $\Phi (X)$；
2. 然后再命令 $A$ 按照 $\Phi (X)$ 来实际制造 $X$，并把其中的 1 份 $\Phi (X)$ 拷贝去掉；
3. 最后，$C$ 会把 $X$ 和剩下的那份 $\Phi (X)$ 捆在一起，并把它们从机器 $A+B+C$ 的组合中间分离出去，这样一来，我们就制造出了 $X+\Phi (X)$ 这样的组合。

按照以上原理，如果我们用 $(A+B+C)$ 来代替 $X$，并进行上述同样的操作的话，那么 $(A+B+C)+\Phi (A+B+C)$ 的自动机组合，就可以制造出自动机组合 $(A+B+C)+\Phi (A+B+C)$ 出来。因此，自动机自复制得到了实现！

Arthur W. Burks 对过程细节的阐述

过程细节如下：

1. 现有自动机 $(A+B+C)$，并附有它的描述 $\Phi (A+B+C)$。
2. 从 $(A+B+C)+\Phi (A+B+C)$ 开始复制流程。
3. $C$ 控制 $B$ 拷贝两份描述，得到：$(A+B+C)+\Phi (A+B+C)+\Phi (A+B+C)$。
4. $C$ 命令 $A$ 按照 $\Phi (A+B+C))$ 来实际制造出 $A+B+C$，得到 $(A+B+C)+(A+B+C)+\Phi (A+B+C)+\Phi (A+B+C)$。
5. 最后 $C$ 把新得到的自动机 $A+B+C$ 和它的描述 $\Phi (A+B+C)$ 捆在一块，并把自己和新自动机分开，这就得到 2 个 $(A+B+C)+\Phi (A+B+C)$；复制完成。

关于非循环论证的说明

这个过程并不是循环论证：我首先把 $A$ 和 $B$ 做了清楚的定义。在我提到 $X$ 之前，我已经说明，$C$ 可以适用于任何形式的自动机 $X$。接下来定义了一个变量 $X$，它描述了 $C$ 将要怎么做，然后，我再让这个变量 $X$ 和 $C$ 产生联系。所以，$A$、$B$ 和 $C$ 的定义是完全独立于 $X$ 的，在此之后，我再让这个 $X$ 指代 $A$、$B$ 或者 $C$。因此，整个过程并非循环。

各组件能力分析

以上的通用构造器（general constructive automaton）$A$ 具有一定意义上的创造力，也就是说，$A$ 可以从抽象的描述来 “制造” 出实体的机器来。同样的，通用拷贝机 $B$ 也有一种能够把一份描述变成两份的 “创造能力”。但 $A$ 和 $B$ 都不具备自复制能力，此外，控制器 $C$ 也远远没有具备任何形式的创造或复制能力，它唯一能做的就是刺激其它的两个组件去做一些事情，把一些东西连接在一起，或者把一些东西从原来的系统中分割出去。然而，一旦 $A$、$B$ 和 $C$ 组合在一起，它们作为一个整体却能够复制自身。故而我们可以把一个自复制系统分割成不同的部分，每一个部分虽然都不能够复制自身，但对于自复制机器整体却又都是必不可少的。

自复制自动机的进化

我们还可以进行如下操作：让 $X$ 代表 $A+B+C+D$，这里 $D$ 代表任何自动机。那么 $(A+B+C)+\Phi (A+B+C+D)$ 就可以制造出 $(A+B+C+D)+\Phi (A+B+C+D)$。也就是说，我们的自复制机器不仅能够复制自身，还具备顺便生产出其他组件 $D$ 的能力。这正是任何自复制生命都具备的功能：在自我复制的过程中，还会产生副产品。

自复制定义与变异的探讨

作为一个系统，$(A+B+C+D)$ 可以经历类似变异的过程。在界定“自复制”的确切含义时，我们会面临这样的难题：有些结构，例如晶体的生长，从某种程度上看也是在复制自身，但我们通常不会将晶体视为真正意义上的自复制结构。有一种方法可以解决这个问题，那就是将发生变异的能力，以及制造与母体相似但不完全相同的“生命”的能力纳入“自复制”的定义范畴。

变异对自复制自动机的影响

现在来分析 $(A+B+C+D)+\Phi (A+B+C+D)$ 这个自动机。“变异”指的是其中某个零件发生随机变化。如果是 $A$、$B$ 或者 $C$ 的某个零件发生变化，那么系统通常会丧失自复制能力。例如，当 $C$ 的一个零件被修改后，$C$ 很可能无法在恰当的时间向 $A$ 和 $B$ 发送刺激信号，或者在需要的时候无法进行连接和分割操作，这种变异是致命的。

然而，如果变异发生在描述 $\Phi (A+B+C+D)$ 上，那么系统制造出的就不再是完全相同的自身，而是修改后的自身。下一代自动机能否继续复制取决于变异发生的具体位置。如果 $A$、$B$ 或者 $C$ 发生变化，子代自动机就会失去继续复制的能力（“绝后”）。但如果变异发生在 $D$ 的描述上，那么除了 $D$ 变成 $D’$ 之外，变异后的子代与母体系统基本相同，之后的子代会继承这个变异 $D’$。这便是可遗传变异的基本过程。

总结

总之，尽管这套系统还处于非常原始的阶段，但它已经具备了可遗传变异的基本特性。大多数随机变异是致命的，但偶尔也可能出现非致命甚至可遗传的变异。这是遗传所特有的性质，而这套自动机系统同样拥有了这一特性 。

Jake 点评：

1、自指 —— 一条永恒的金带

自指是一个非常古老的话题，它通常与古代奥义以及各种神秘哲学有关。例如佛教中所提倡的 “观身无常、观心无我”，以及古希腊的 “认识你自己”，都在劝解人们能够将心智的观察箭头指向自己。中国道家所倡导的 “无”，正是一个最简单的一字悖论。

自噬的蛇

一幅最能体现自指深邃含义的图画莫过于这条正在吞噬自己的蛇。此蛇作为一种图腾曾广泛出现在北欧神话、基督教神学、印度教和非洲宗教之中。这条蛇将自指那种深刻的自我毁灭性体现得淋漓尽致 —— 我们可以想象一下当它把自己吞噬完毕会产生怎样怪异的情景。

将这种自我毁灭性的古代奥义应用到现代科学中已经产生了一系列深刻的结论。首先，在 19 世纪末，著名数学家康托尔（George Cantor）将 “对角线删除” 法则应用到集合论中，从而证明了实数的个数比自然数多。紧接着，罗素（Bertrand Russell）提出了著名的 “罗素悖论” 而摧毁了弗雷格（Gottlob Frege）的数学大厦。年仅 25 岁的哥德尔（Kurt Gödel）巧妙地应用同样的破坏性自指一举摧毁了数学大师希尔伯特（David Hilbert）的完备一致性的数学体系梦想。图灵（Alan Turing）则利用同样的技巧进一步发现任何超级计算机都不可能求解的图灵停机问题。

纽约时报曾将哥德尔不完备定理评价为 20 世纪最伟大的数学定理。自指可以用来构造破坏性的悖论已经是众人皆知、司空见惯了。然而，这种认识其实很片面。自指包含了比自指悖论更宽泛的内容，因为在自指大家庭中，还包括另外一类构建性的成员。

1953 年，正当人们举杯欢庆沃森和克里克发现了 DNA 双螺旋结构，并从分子层面上解释了生命的自我复制之谜的时候，另外一名伟大的美国匈牙利裔数学家：约翰。冯诺依曼（John von Neumann）正在独立地思考着生命自我复制的逻辑基础。然而，令人遗憾的是，那时的冯诺依曼已经患上了癌症，并于 1957 年的 2 月去世。于是，他的助手阿瑟。伯克斯 Arthur Burks 将他关于自复制自动机理论的整理成书《Theory of Self-reproducing Automata》，并于 1966 年出版。

与沃森。克里克不同的是，冯诺依曼要寻找的是生命自我复制的逻辑基础而非物质基础。虽然冯诺依曼没有明确指出，但是已经暗含了这个自复制的逻辑基础不是别的，正是一种自指结构。也就是说，自指恰恰是生命实现自我复制的逻辑内核。 这也许会让读者感到困惑。不是说，自指都是用来构造诸如哥德尔定理、罗素悖论之类的破坏性武器吗？实际上，还存在着另外一大类自指，笔者称之为 “建构性的自指”，它不但不会引起破坏，反而能够创造很多令人意想不到的惊奇结构。至于自我繁殖的系统是如何令人意想不到的，请参考第 4 节的讨论。

实际上，早在 1938 年，与哥德尔共同奠定递归函数论基础的数学家克林尼（Stephen Kleene）就证明了递归函数论中的一个著名定理：递归定理（更精确地说，应该叫 Kleene 第二递归定理）。根据它，人们可以很轻松地得到一个数学推论，系统的自我复制是可能的。证明递归定理的核心技巧，是一个被称为 “蒯（kuai3）恩” 的特别技术。蒯恩（Willard.V. Quine）是美国的哲学家，终身致力于哲学、数理逻辑、集合论的研究。他创造了一种称之为蒯恩的方法，使得人们可以不通过使用 “我” 或者 “这句话” 等词语就能创造出可以谈论自身的句子来。

有趣的是，蒯恩构造恰恰就是那条 “黄金对角线”（这一方法正是当年康托尔最早提出证明实数比自然数多的方法，也是哥德尔定理构造哥德尔句子的关键技术）。只不过，康托尔、哥德尔等人的对角线与蒯恩的对角线方法稍有不同。我们会在第 6 节中详细地讨论这些技术。

总而言之，从宗教到科学，从悖论到自复制，自指是贯穿始终的主题。正如《哥德尔、艾舍尔、巴赫》这本书指出的那样，自指是一条永恒的金带。

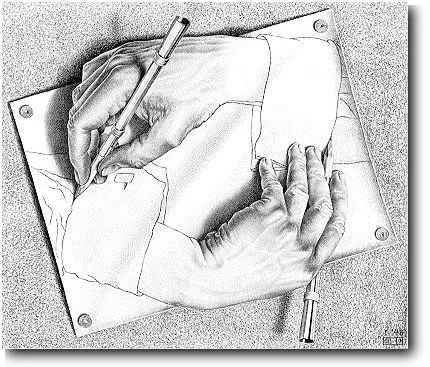
画手，艾舍尔（Maurits Cornelis Escher），荷兰著名版画艺术家

图片来源：《魔镜 —— 艾舍尔的不可能世界》

2、蒯恩程序

于是，一切的矛头都指向了这个神奇的复杂度阈值，它到底是多少？虽然冯·诺伊曼到死也没有给出任何关于复杂度的计算，但是他用一名数学家和哲学家敏锐的头脑，深刻地指出了其实这个复杂度阈值与数学、逻辑学以及哲学上的一个重要概念 “自指” 有关。

冯·诺伊曼在本章最末部分所讨论的能够自复制的自动机的抽象描述：$(A+B+C)+\Phi (A+B+C)$ 其实就是一个哲学家们称之为 “蒯恩” 的程序。蒯恩（Willard.V. Quine）是一位美国的哲学家，他创造了一种称之为蒯恩的方法，使得人们可以不使用 “我” 或者 “这句话” 等词语就能创造出可以谈论自身的句子来。例如下面这句话就是一句不使用 “这句话” 的自指悖论：

把 “把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变得到的句子是假的” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变得到的句子是假的

当你按照这句话的指示将引号中的文字放到引号后面的时候，你就得到了一句自我否定的句子，所以上面那句话与下面的话等价：

这句话是错的

之后，数学家 Kleene 将蒯恩这种语言上的操作进行数学化就得到了一种更加普适的 Kleene 递归定理。有了这个递归定理以后，数学家就可以在严格的数学公理体系中玩各种各样的自指游戏。之后，哥德尔利用这种技术构造了公理系统中著名的哥德尔句子 “本命题不可证明”，从而推出了哥德尔定理这个被《纽约时代杂志》评选为 20 世纪最伟大的数学定理。

那么，究竟这个蒯恩程序是什么呢？其实，它非常容易理解，它就是一个能够把自己的源代码打印出来的程序。

S(x){
    q='S(x){\n q=\'\'+q+\' \';\n Print(\'\'+p(q)+\' \');\n}';
    Print('S(x){\n q=\'\'+q+\' \';\n Print(\'\'+p(q)+\' \');\n}');
}

这里面的 “\n” 表示换行符，即如果执行 Print('A\nB')，则程序会输出下面的字符串：

A
B

“+” 表示将两个字符串进行串联形成一个新的字符串，例如 A = '123', B = '456'，则 A + B = '123456'。

这个自打印程序调用了一个简单的解码函数 p(q)，p 的作用是将字符串 q 变换成更浅一层次的字符串。例如，如果 q 是 '\\'\\n\\'，那么 p 这个函数就会计算输出 '\\n'。也就是说 p 完成了一组映射：它把 '\\' 映射成 '\'，把 '\\'' 映射成 '''，而把 '\n' 映射成回车符。显然 p 是可以写出来的。大家可以利用 Java 或者 VB 来实现这个程序，运行它就会发现它能够自我复制。

让我们来分析一下这个程序是如何运作的。首先，看程序的最后一行，即

Print('S(x){\nq=\'\'+q+\' \';\n Print(\'\'+p(q)+\' \');\n}');

这句话的作用是让程序在屏幕上打印出一个字符串。注意观察，这个被打印出的字符串其实是由 “+” 号被分割成了 5 个部分：

• 第一部分：是 'S(x){\nq=\''
• 第二个部分：是 q 这个字符串的原封不动的拷贝
• 第三部分：是字符串 ' \';\n Print(\''
• 第四部分：是函数 p 作用到 q 上面的结果即 p(q)
• 第五部分：还是一个字符串 ' \');\n}'

然后当我们把 q 字符串的数值代入第二部分和第四部分，并进行运算 p 之后，就得到了和源程序一模一样的结果。你不妨在计算机上运行这段程序，就会发现这段程序会在屏幕上赤裸裸地把自己的源代码打印出来。

我们不妨把这段程序的 5 个部分进行归并，写成由下面的三部分构成的 Copy.Popup.Control，其中：

• Copy 就是 5 部分中的第二部分，即相当于一个拷贝字符串的程序，你输入给 Copy 什么字符串，Copy 就会把那个字符串再原封不动地吐出来；
• Popup 这部分就是原来的 5 部分中的第四部分，即函数 p，它的作用相当于一个弹出操作，也就是为输入的字符串脱去一层引号。如果输入的字符串原来是在第 n 层虚拟世界，则 Popup 的作用就是让字符串跳到第 n - 1 层；
• 最后 Control 这部分就相当于原来的第 1、3、5 这三部分以及最一开始的语句 Print 的总合，它的作用就相当于是为 Copy 和 Popup 制造出来的字符添加适当的连接词，使得最后的字符串能够拼接成与原来的程序一模一样的源程序，并将其打印到屏幕上。

所以这句 Print('S(x){\n q=\'\'+q+\' \';\n Print(\'\'+p(q)+\' \');\n}'); 就可以改写成 (Copy.Popup.Control)(q)，其中 “.” 表示将不同的程序连接为一体。

如果我们把一个计算机程序 X 的描述（或者称源代码）写为 \varPhi(X)，则自打印程序的第一条赋值语句就相当于给 q 赋予了 \varPhi((Copy.Popup.Control))，即 (Copy.Popup.Control) 这三个程序连在一起的源代码。最后我们可以将自打印程序简写为：

S(x){
    q = \varPhi(Copy.Popup.Control)
    (Copy.Popup.Control)(q);
}

那么，观察这个程序，就会发现实际上它就是冯·诺伊曼所说的那个自复制程序：((A + B + C) + \varPhi(A + B + C)) 了。在这里：

• Copy 就相当于冯·诺伊曼程序中的拷贝器 B，它能将输给它的数据原封不断地再打印出来；
• Popup 就相当于冯·诺伊曼说的通用构造器，它能够根据一段数据而把数据对应的自动机的源代码打印出来（这相当于从描述中构造出自动机）；
• Control 这部份就对应了 C；
• 而 q = \varPhi(Copy.Popup.Control) 就对应了描述：\varPhi(A + B + C)。

因此，我们实际上可以很容易地用我们的个人电脑实现自复制的计算机程序。

你也许会提出这样一个质疑，即使是这个蒯恩程序也没有实现真正的自复制。因为这个程序仍然需要调用一些字符串处理程序例如函数 p，以及字符串运算符 “+” 等等，而这些功能并不是这个程序自己完成的，而必须借助比它更高一层的编译器才能完成。于是，这个蒯恩程序实际上已经与一个平庸的自复制程序（例如就包含了一个平凡的高层次语句”Copy me”）没有任何区别了，只不过对于平庸的自复制程序来说，我们为自复制的环境赋予了过高的能力，而自复制程序本身只起到一个触发器的作用。而对于蒯恩程序来说，翻译蒯恩程序的环境变得相对简单一些，但是实现自复制的代码就要承担更大的责任。原则上讲，我们的确不能做出来一个完全不借助于环境，而凭空实现自复制的机器。但是，我们总可以降低对环境的要求，把编译器的复杂度变小，从而凸现出自复制程序的能力来。

由此我们可以看出，在不同的情况下，编译环境和在此环境下实现的程序会呈现出连续的复杂度变化。而自复制程序实际上是对环境的复杂性和程序本身的复杂性的一种折衷。因为如果环境的复杂性越高（编译环境可以支持很复杂的指令集合），要实现一个可以打印自身源代码或者复制自身的程序就变得很简单（程序自身的复杂度下降）；反过来，如果环境的复杂度越低，那么你要实现一个自复制的程序也会变得越困难。于是，我们可以得到下面这张图：

如图所示，如果我们把一切程序按照它所运行的编译环境以及它自身的复杂程度列出这样一个连续的空间，那么在不同的编译环境下的自复制程序就会近似地形成一条如图的直线。我们可以肯定地知道，它是一条单调下降的曲线，因为随着环境复杂度的升高，要实现自复制的程序的编写也会变得越来越轻松。所以，我们大概可以估计出来这样一个自复制程序所满足的复杂度方程：

上述公式表示了实现自复制程序的复杂度的允许条件，当等号成立时，它就对应了图中的向下的直线。不等式对应了直线右上角的半平面。这个式子让我们联想到了第二章提到的不确定性原理。因此，自复制程序的复杂度讨论也许的确存在着类似量子理论中的不确定性原理。这种从不同层次来考虑程序复杂度的概念也许真的蕴藏着我们尚不知道的真理。

总之，我认为自复制自动机才真正抓住了人们常说的 “涌现” 这个关键概念的本质。 因为从单个组成单元来看，无论是通用构造器 A，还是拷贝器 B 还是控制器 C，以及它们的数据 Φ(A+B+C) 都不具备自复制的功能，而当把它们恰当地合在一起的时候，它们的确可以实现自复制，从而实现了自复制功能的涌现。与其它对涌现的机制讨论的不同之处在于，自复制自动机具有相应的数学对应物：递归定理， 因此我认为如果要从数学上理解涌现，自复制自动机是绕不开的。只可惜，冯・诺伊曼的最终梦想：从热力学和信息论的角度来理解自复制自动机的自发涌现仍然没有实现。

---

自指的演化：物质、符号和语义闭包

原创 Howard H. Pattee 集智俱乐部 2023 年 04 月 04 日 18:48 北京

导语

系统如何实现自复制？冯・诺伊曼敏锐地察觉出一个规律：只输出符号的机器无法构造机器，只输出硬件的机器无法构造符号。这是所有自指机器都需要面对的一个难题，也正因为如此，自指需要同时兼顾物质与符号。由此，本文作者 Howard Pattee 提出了「物质 - 符号互补理论」，以全新的方式定义自指系统，并在此基础上深刻讨论了符号、物质、物理规律和自组织。本文可能确实晦涩，但值得深入思考。

—— 章彦博

关键词：物质 - 符号互补理论，语义闭包关系，涌现演化，开放式演化，自指

Howard H. Pattee | 作者

杨明哲 | 译者

章彦博 | 审校

梁金 | 编辑

文章题目：

• Evolving Self-reference: Matter, Symbols, and Semantic Closure
  First Online: 01 January 2012
   
  https://link.springer.com/chapter/10.1007/978-94-007-5161-3_14

摘要

关于涌现演化（emergent evolution）或开放式演化（open-ended evolution）的理论要与物理理论的认识论基础和自指逻辑相一致。为了理解这种演化，需要在事件的物质和符号方面进行互补的描述。我们基于两点来解释物质 - 符号互补理论（ matter-symbol complementarity）：自复制的逻辑，和物理法则与初始条件的区别。物理法则和自然选择是事件的互补性的模型。物理法则描述了有机体无法控制的不变事件。自然选择下的演化是关于有机体如何增加对事件控制的一种理论。我定义了一个必要的语义闭包关系（semantic closure relation），将具有开放式演化能力的有机体的物质和符号方面联系起来。

1. 什么是自指

自指（Self-Reference）有许多含义。在符号系统中，如逻辑和语言中，自指可能会导致众所周知的模糊性和表面上的悖论，例如，“本句话是错的”。在物质系统中，例如分子和机器，自指并没有明确定义，但可以描述诸如自催化循环、反馈控制和振荡器等因果循环。在认知层面，自指发生在内省中，通常认为是意识的一个方面。我定义了一种特定形式的自指，适用于有机体的物质和符号方面之间的闭合关系。我认为这种自指观点对于理解从生命起源到认知水平的所有组织层次上的开放式演化、发展和学习都是必要的。这不是一个全新的观点，而是对物理学、逻辑学、计算理论、分子生物学和演化理论等多个成熟领域的思想进行细化和整合的结果。

简言之，具有开放式演化潜力的自指，指的是物质方面动力学（物理定律）和符号方面约束（句法规则）之间的自洽闭包。我将这种自指关系称为语义闭包（Pattee, 1982）。这是因为，要使由物理定律决定的物质具有功能性（即具有生存价值、目标、意义、自我意识等），就必须将其与自由选择的符号（物质符号的一面）融合起来。语义闭包需要物质和符号两个方面的互补模型。前述简短，容我细细道来。

图 1. 比利时画家 René Magritte 作品《这不是一只烟斗》，一幅有着自指意味的艺术品

我曾在很多文章里强调过（例如，Pattee, 1969, 1972, 1982），物质 - 符号划分（matter-symbol distinction）不仅仅是定义生命的一个客观基础，更是开放式演化的一个必要条件。我的推断不仅基于生物学上的事实，还基于对物理理论的原则性认知需求。换换句话说，我要求生命系统的模型必须在认识论上与物理和逻辑原理一致。众所周知，复制和演化很大程度上取决于生物体的物质行为如何受到符号记忆的影响。比如在生物学上，物质行为对应的是生物的表现型，符号记忆对应的是基因型。而在计算机领域这就是硬件和软件的区别。哲学家把这种划分上升为脑 - 心智问题。大多数人不知道的是，即使是在物理理论的公式中，物质 - 符号划分的形式也是必要的，即分清楚物理法则和初始条件。我会在第 4 节进一步阐述。

冯・诺依曼（von Neumann）第一个认识到物质 - 符号互补理论在逻辑上的必要性。他在自复制自动机（self-replicating automata）的讨论中提及了这一点（1966）。自复制自动机这个机器有能力制造出越来越复杂的自动机。这一点常被称作涌现演化。冯・诺依曼曾指出，在普通用法中，物质和符号是不同的类型。举例来说，神经元产生脉冲，但脉冲与神经元不属于同一类型；计算机生成比特，但比特与计算机不属于同一类型，测量设备产生数字，但数字与设备不属于同一类型等等。他指出，通常设计用于输出符号的硬件机器无法构建另一台机器，而设计用于构建硬件的机器则无法输出符号。这只是对实际机器和自然语言使用的简单观察，并非本体论或二元论的断言。冯・诺依曼还观察到，复杂性有一个 “完全决定性的属性”，一个阈值以下的组织会退化，而阈值以上则可能出现开放式复杂化或涌现演化。他用通用计算做类比，提出达到这个阈值需要一台通用构造机，可以根据机器的符号描述输出任何特定的物质机器。如果通用构造机提供了自身的描述，并且有办法把该描述复制和传输到一个新构造的机器上去，那么自复制在逻辑上就是可能的。

图 2. 科学家冯・诺伊曼（von Neumann）

与通用计算机相似，为了避免自指的歧义，需要在机器和机器描述之间做出分类上的有逻辑的区分，无论这个机器是物质机器还是仅仅是形式机器。为避免自指歧义，需要有两个逻辑类型或范畴。这是符号 - 物质划分的逻辑基础。他的所谓的动力学模型需要具有符号功能（例如逻辑功能）和物质功能（例如切割、移动等）的原始部件。我将在第 9 节讨论这个论点。至于这些符号和物质功能是如何产生的，冯・诺依曼没有给出答案。他认为，“它们在世界上出现本身就是一个巨大的奇迹。” 这是生命起源的问题。

2. 什么是物质

针对我的论证，我将把物质和能量理解为通常物理定律中使用的概念。这些定律描述的事件会尽可能的独立于观察者，即独立于初始条件。直到我们通过测量提供了初始条件，这些定律才具有意义。定律和测量是必须区分的范畴。定律并不进行测量，个体才会进行测量。测量是一种有局部意义的有意行为，因此也涉及符号的一面，通常以数字记录的形式出现。这是物质 - 符号划分的物理基础。我将在第 5 节详细阐述这一点。在实践中，划分物质的物理方面和符号方面已经很成熟了，我们也很容易识别两者。无论是物质还原主义者还是形式主义者，在实践中，很容易区分物理定律对物质的描述，以及语法规则、程序对符号的描述。此外，我们都知道制定理论、构建仪器、进行测量和计算之间的区别。

当我们试图去描述这些互补的物质和符号的关系时，困难就出现了。传统哲学认为，描述这些互补的物质和符号的关系是指涉的问题，或者符号如何代表物质结构的问题（例如，Whitehead, 1927; Cassirer, 1957; Harnad, 1990）。但我认为，更基本的问题是物质结构如何成为符号。从生命起源和进化的角度来看，最困难的问题是：面对没有功能和意义的物质，语法规则是如何逐渐驾驭它们，为其赋予功能与符号意义的？（例如，Pattee, 1969; 1992）。我在这里不会过多探讨符号起源的问题。有几个原因，一是由于其难度，人们不认为符号起源是哲学或科学任何领域的核心问题之一。另一个原因是对于大多数科学模型来说，不必知道符号的本质或起源。自然语言、逻辑、数学符号系统和计算机通常被简单地视为成熟的工具，对于大多数模型而言，没有必要问它们是如何产生的。

3. 物质 - 符号互补理论 —— 既非还原论也非二元论

出于历史上的原因，生物学家的思考方式要么是还原论（reductionism），要么是二元论（dualism）。我不这么看。作为一个物理还原论者，我相信所有的符号行为都一定有真实世界对应的物质行为，且遵循物理法则的约束。举个例子，DNA 的化学结构和化学反应一定和它基因遗传的功能相关，感光乳剂的化学结构和和化学反应一定和它的测量功能相关，以及神经元的生化过程一定和感知与心智相关。对于理解符号系统来说，还原到物质世界来解释一定是必不可少的一步。

图 3. 胶片中的感光乳剂

虽然我是一个还原主义者，但我不相信符号 “只不过” 是物质的说法。“只不过” 意味着，对符号系统的完整理解只需要一个完整的物理法则模型。还原主义者们很乐意看到高层次现象背后的物理关系被挖掘出来。但我认为，哪怕在细节上做到极致，也没有一个完整的物理模型可以把符号功能彻底解释清楚。简单来说，这是因为符号功能不是物质载体或物理法则的固有属性，就像所有的生物学上的功能。它是大量个体针对特定的情况，使用符号描述物质结构或者控制物理行为过程中，自然选择出来的属性。换句话说，单一的物理模型不足以描述功能或意义。所以互补性的模型是必要的。我会在第 4 节详细阐述这一点。

我想强调的是，我的立场不是源自这种形而上学的观点，而是源自物理学家和生物学家实际建模的方式。从历史上看，还原论和二元论的争议一直没有什么成果，同时又非常的棘手。所以，与其试图澄清这个问题、确定哪个模型更为准确、解决不可判断的形而上学问题，我更想专注在互补模型上。我会详细阐述使用互补模型的好处。互补模型在物理学中是众所周知的。粒子和波，微观和宏观，决定性和随机性，粗粒度和细粒度，可逆和不可逆的模型对于完全理解任何复杂系统都是必要的。Rosen（1977）更用 “有效描述系统行为所需的模型数量” 来量化系统复杂性。

4. 什么是测量

我认为，物理学中的测量过程，是证明语义闭包的互补模型必要性最令人信服和最基本的例子。一方面，我们可以描述测量装置的物质细节，这在设计和构建中可能是必要的。另一方面，如果测量装置要发挥其功能（即产生符号记录），则这些细节必须被有选择地忽略。这不是形而上学的立场，而是源自实用主义的事实，即：要获得有意义的结果，我们必须能够测量某些东西而不必测量一切。这意味着，为了发挥作用，测量装置中的物质自由度必须要减少。它的数量要减少到，与描述结果的那几个语义相关符号的自由度数量一致。如果没有这样的分类过程，我们就会陷入一个发散的、无限递归的测量，正如冯・诺伊曼（1955）指出的那样。

图 4. 测量证明了互补模型的必要性

一个生物体如果必须要对环境进行分类才能生存，那就可以运用这种测量的概念。在物理理论中，物质行为和符号行为之间的区别是非常明显的，我将在第 5 节中进一步解释原因。然而，在原始生物中，并不容易区分物质和符号。这一现象在有机体中的结构 - 功能关系中的都能看到。我们作为建模者，需要了解 DNA 的详细化学结构，以便理解其功能的化学相关性并设计相应模型。然而，在细胞中，只有对基本序列进行分类才与蛋白质的合成相关，这是 DNA 在细胞中的语义功能。就像测量装置的情况一样，从真实密码子的许多自由度到它实际传达的少量语义，信息大大减少。同样地，在蛋白质水平上，任何外部的物质折叠结构模型都需要大量的细节和计算能力。但是在细胞中，蛋白质的折叠是一个物理过程，只需要合成氨基酸的线性序列，不需要其他描述或指令。在所有情况下，从我们的建模角度来看，当我们需要将结构与功能联系起来时，我们不能忽略多级描述。但更客观的是，细胞的一些行为（如阅读基本序列）是符号性的，但大多数行为（如蛋白质折叠）却不是。也就是说，DNA 只符号性地描述氨基酸的线性序列，而物理定律则负责折叠、自组装和催化。

图 5. 蛋白质折叠示意图

就像测量一样，基因为了具有任何有用的功能，必须能够符号化某些东西而不是符号化一切。否则，基因指令将永远不会结束。如果没有简化，可遗传的符号将遭受与测量符号一样的无限递归。因此，为了允许物质复杂性的开放式增长，同时保持可遗传性，需要对描述进行简化。用常规的语言来说，符号化某些东西而不符号化一切被称为分类（classification）。因此，具有潜在涌现演化潜力的组织，它们超过了冯・诺伊曼的复杂度阈值，它们必须进行自主分类。

5. 什么是符号

符号很难用任何简单的方式来定义，因为符号具有功能，而功能不能孤立地归于局部结构。符号的概念，就像更一般的功能概念一样，离开了整个符号系统的上下文就没有固定的含义了。因此，为了实现特定的功能，例如分类、控制、构造、通信、决策和模型构建，我们还需要考虑构造(写入) 和解释(读取) 符号的物质组织(例如，Pattee, 1969) 。所有这些活动只有在特定的背景下才能被确定为功能，从个体的局部目标到物种的全球生存都是如此。符号载体只是自我指涉的大型组织中的一个小物质结构，但符号功能却是组织生存和演化的重要组成部分。这种自主的结构 - 功能自指组织就是我所说的语义闭包。

在这次讨论中，我可以用另一种方式来描述符号，即将其视为一个相对简单的物质结构。虽然符号可以用所有常规的物理定律正确描述，但它具有的意义或语义功能却不能被这些定律所描述。物理定律无法描述符号的功能或任何功能，是因为我们特别将其限制在仅描述某些物质属性上。这些属性应符合不变性和对称性原则，尽可能独立于观察者和个体测量，正如我在第二部分中所述的那样。这是保障物理定律普适性所必需的。相比之下，符号是在很少的物理限制下产生的，但最终是根据它们对局部环境中个体的生存贡献而被选择的。换句话说，只有那些对个体没有意义的普遍且内在的物质方面才被定律描述，而那些对局部环境中个体具有意义的上下文相关的、选择性的方面则被我们描述为符号（Pattee，1982）。当然，所有符号的物质载体都需要遵守物理定律，但符号功能需要另一种模型，即互补模型，而不是二元论。

物理理论不能将符号简单地视为由定律描述的物质。要理解这一点，就必须要认识到：物理定律的概念，只有在我们讲将经验分为不变的、和变化的两类时才有意义。这个区分是定律和初始条件的定义之一（Wigner，1964）。此外，只有因为符号和物质方面的独立性，物理定律才能用最小的模糊度建模，以区分受物理定律支配的世界和形式上的模型。换句话说，符号方面的独立性允许清晰、基本的定律和初始条件之间的分离。如果没有物理定律和初始条件的明显分离，对称、不变和守恒原则没有什么意义（例如，Houtappel、Van Dam 和 Wigner，1965）。在物理学中，对初始条件的测量是符号模型与物质世界唯一的接触方式。只有在经过测量提供特定的初始条件之后，定律才有意义。因此，符号必须被视为属于一般的初始条件类别，这也包括边界条件和约束。普通的初始条件没有规律，但符号是特殊的约束集合，允许我们通过规则来描述符号行为。

符号行为不能用定律描述的另一个解释是：我们要求定律是完备、且不可变化的。因此，我们不能修改或调整定律行为本身 —— 定律之中没有选择的空间。在由确定性定律描述的系统中，我们唯一能使用的手段是测量和控制初始条件。书写符号是一种时间相关的动力学过程，却留下了一个时间无关的结构或记录。数学家 Emil Post（1965）将符号的书写描述为 “时间过程凝固成空间特性”。当这些结构再次成为约束条件进入定律的动力学时，符号就被读取了（Pattee，1972）。任何高度发展的形式符号系统都可以被看作是各种各样的初始条件或约束条件的集合，通常存储在记忆中，通过局部选择的规则而非物理定律，产生有意义的或功能性行为。这意味着物质符号载体的操纵规则应该尽可能独立于质量、能量、动力学时间和速率。基因密码、自然语言、逻辑、形式数学和计算机编程语言是这种符号系统最著名的例子。正如我所强调的，所有符号系统都必须具有符合物理定律的物质实体。但是，出于上述原因，即使符号在物理定律层面的描述符合所有细节，也无法揭示符号本身的意义。

6. 什么是符号模型

任何模型都必须在某种程度上表现出与其所模拟的对象相似的行为。物理使用符号来建模，符号与对象的相似性，通过在它们的部分行为间建立类比关系来确定。其中对象的行为由无情的定律支配，而符号行为则由局部的数学或计算规则所决定。

由于符号的物质载体可以是任意的物理结构（例如：能量简并），其规则源于边界条件而不是来自于物理定律。因此，符号模型具有一个特征：除了少数几个被选择的平行方面外，物质系统和符号模型之间通常没有其他相似之处。对于符号模型，我们唯一可以期望的是，符号模型和对象在一些特定方面具有相似的或可预测的行为。

赫兹（Hertz，1894）是第一位清晰地阐述了物质与符号之间关系的现代科学家：“我们形成外部对象的图像或符号；我们形成它们的方式是这样的，图像逻辑的必然结果无论何时都是相应对象物质的必然结果的图像。” 然后，为了强调形式符号模型的有限指代领域，他补充道：“对于我们的目的来说，它们（符号）在任何其他方面都不必与事物（物质）相符。实际上，我们不知道，也没有任何手段知道，除了这一基本方面以外，我们对事物的概念是否还与符号一致。” 值得注意的是，通过将前两个 “图像” 的替换为 “指令”，并将最后一个替换为 “构造”，我们就得到了对遗传密码功能的简洁描述。

图 6. 物理学家赫兹（Hertz）

7. 如何避免物质 - 符号问题

每个科学文化都有其忽视物质 - 符号问题的原因。物理学中，物质和符号之间有一个明确的范畴区分，因此通常不需要一个符号理论，即使用数学符号系统表达的理论在物理学中扮演着主要角色。此外，物理学家研究的物质系统在大多数情况下本身不包含符号活动和功能。测量初始状态通常被视为一种原始的过程，即从物质映射到符号。幸运的是，我们不需要一个符号理论也能得到有用的符号结果。然而，在一些著名的思想实验中，例如麦克斯韦妖和吉布斯悖论，需要明确规定何时完成测量，这时物质 - 符号问题就是不可避免的了（例如，Leff 和 Rex，1990）；在量子理论中，即便在定律中已经包含了测量过程，对于测量的解释仍然难以捉摸（例如，Wheeler 和 Zurek，1983）。在任何情况下，符号和测量过程的演化起源都不被当成物理学中的主要问题。

图 7. 麦克斯韦妖示意图

由于所有生物体都依赖内在的符号控制，而生命起源需要符号化的遗传密码作为关键步骤，因此生物学家应该对物质 - 符号问题更感兴趣。然而情况并非如此。大多数生物学家都是物质还原主义者，他们只寻求与符号活动和功能相关的物质结构的发现，这是他们唯一的解释层次。因此，在生物学中，实验或物质发现扮演了主要角色，而不是理论。例如，生物学家认为发现 DNA 的化学结构和编码的分子基础足以描述和解释基因符号行为。这种物质还原主义甚至扩展到了认知活动，许多人认为发现思维背后的神经和相关物质就足以解释意识行为（例如 Crick，1993）。

传统上，哲学家关注的是更高层次的身心问题，但他们也建立了一些形而上学立场，有效地将物质 - 符号问题最小化，如唯心主义、二元论、物质还原主义、功能主义以及最新且最有效的计算主义。除了传统的哲学、物理学和生物学文化外，第四个基于计算机的文化包括经典的人工智能领域（例如 Newell，1980; Pylyshyn，1984）和更近期的人工生命领域（例如 Langton，1988）已经采用可编程计算机作为通用符号模型。这种文化明确地忽略了计算机本身或它所模拟的东西的物质体现。人工智能和人工生命都通过接受功能主义或更强的计算主义观点来避免物质 - 符号问题。像经典的物理主义一样，功能主义和计算主义也对物质和符号进行了明确的区分，但它们只关注符号类别。功能主义者从一个半对半错的角度辩解：既然对于任何符号功能都有无数种可能的物质体现，那么符号与物质的关系就是毫无理由且任意的。他们认为，生物和心理行为的特定事实仅代表一种可能的物质体现，而计算机原则上也可以同样好地代表另一种物质体现。换句话说，功能主义者认为符号活动的特定物质体现并不重要。

功能主义模型的要求听起来好像是基于物理系统模型一样的经典原则，即选择计算机模型行为的某些方面必须与生物体行为的某些方面相似。计算主义者的要求也类似，只是 “功能” 这个词现在具有了正式的符号意义。计算主义者模型的主要要求是：它能计算出与被建模对象的至少一个相同的功能。尽管物理和计算机模型表面上看起来相似，但是他们对于测量的作用和物质符号关系有根本不同的看法。物理学家则认为测量是与世界进行经验接触的唯一手段。因此，他们的可观测量都是精确定义的、相对简单的、可以准确测量的。在物理学中，人们为了设计和构建测量设备以及实际进行测量，付出了巨大的努力、时间和资源。

功能主义者和计算主义者对生物和大脑进行建模时，定义可观察量更为困难。他们的大部分时间和资源都花费在编写和运行计算机程序上，至于他们使用的可观察量，很少能够精确地定义以进行客观测量。人工智能通常对复杂的认知活动进行建模，例如问题解决、模式识别或思维类型。人工生命通常对自复制、适应性和涌现等活动进行建模。这些可观察量不够简单，无法精确地定义或测量。虽然它们的符号操作足够精确，但它们的符号基础是模糊的。由此产生了无法平息的争论，例如计算机中符号和意义的起源（例如 Searle 的中文房间），以及计算机是否具有生命。在第 10 节中，我将提出功能主义的其他不足之处。计算主义者还必须做出一种无端的假设，即所有物质都是计算的，也就是说，如果我们选择将其解释为计算，则要假定每个物质都在计算某些东西。这种主观的观点完全回避了物质 - 符号问题（Pattee，1990）。

图 8. Searle 的中文房间

8. 自组织方法

许多科学家采取了合理的策略，将 “物质 - 符号划分” 视为自发增长复杂性的物质系统的某个后期产物。这种模型通常被称为自组织（self-organization）。早期的文献包括对某些物理系统的讨论，这些系统虽然简单，但却可以自发增长复杂性（例如，Yovits 和 Cameron，1960; Yovits、Jacobi 和 Goldstein，1962）。当时很少有自组织的一般性理论得到全面发展（Simon，1962; Burgers，1963; Pattee，1969; Kauffman，1969）。在 1970 年代，非平衡热力学和非线性动力学模型中发现了新类型的秩序产生（例如，Glansdorff 和 Prigogine，1971; Haken，1977; Nicolis 和 Prigogine，1977）。关于自组织的最新工作收集在 Yates（1987）中。热力学方面的一些发展引发了对可能的组织原理的讨论和推测，涉及对传统新达尔文主义模型的修改（例如，Weber，Depew 和 Smith，1988）。这些组织模型和理论通常仅应用于前生物学（prebiotic）或至少是前符号（pre-symbolic）的物质，因此不涉及物质 - 符号关系。

目前，随着非线性动力学中意想不到的丰富性被发现，自组织现在通常被包括在称为复杂性科学的新领域中（例如，Stein，1988; Nicolis 和 Prigogine，1989; Jen，1989; Zurek，1990; Stein 和 Nadel，1990; Waldrop，1992; Kauffman，1993）。它的潜力有许多来源，包括数学家、物理学家、计算机和认知科学家，每个人都有特定的方法，但彼此重叠。例如，非线性动力学、混沌、元胞自动机、非平衡热力学、统计力学、固体物理、连接机器、人工神经网络等等。即使在这个新的复杂性理论领域中，符号起源也很少被视为一个问题，这个领域中的大多数计算模型都没有清晰地区分基于规则的符号行为和基于物理定律的物质行为，至少没有共识。该领域包括一些物理学家，他们认为我们所有的物理模型都受到测量的符号输出的限制（例如，Wheeler，1990），还有一些计算学家认为所有符合物理定律的物质过程都是计算（例如，Toffoli，1982）。所谓的强人工智能和强人工生命建模者认为，特定的物质表象是无关紧要的，因此，足够逼真的计算机模拟将成为建模的一种实现形式（例如，Langton，1988）。当然，如果一个人相信一切都是计算，或者改进模拟就可以让其成为现实，那就不会看到物质 - 符号问题（Pattee，1988）。在另一极端，有些物理还原主义者只将符号视为一种燃素和以太一样的幻觉，只要有充分物质描述，那符号就没有必要存在（例如，Churchland，1981; Crick，1993）。

9. 演化和认知中的符号功能

如果我们了解蛋白质合成的工作原理，我们可能会得出结论，构建是符号的第一个功能。然而，构建需要对部分进行分类和控制。此外，除非有遗传传递，否则构建对演化没有任何价值。这显然需要进行沟通。换句话说，在原始水平上，这些功能中没有一个可以被孤立为主要功能，甚至无法从客观上互相区分。这是符号和生命起源问题如此困难的原因之一。

在认知层面上，符号使得我们的主观感受与他人的感受可以进行比较，从而赋予了一定程度的客观性。在这里，“客观性” 只是指不同观察者通过交流能够达成基本一致的能力。例如，如果我看到一个绿灯，如果没有符号，我无法告诉另一个观察者我所看到的东西。即使使用自然语言告诉你我看到的是 “绿色”，也不能保证你对 “绿色” 的体验和我的一样。只有通过将复杂知觉抽象为更简单、更普遍的符号分类的测量过程，才能在群体中实现一致和可交流的客观性。这就是 Born(1965) 的基本解释，说明了为什么数学模型对于表示物理理论是必不可少的。它本质上定义了物理学客观性的一个必要条件。然而，这个原则也比那更加普遍。在能够通过自然选择来演化的生物种群中，它们的可遗传符号必须拥有相同的 “通用交流分类”（universal communicable classification）。演化中的遗传传递的要求，从根本上来说就是一个交流问题。

为什么物质结构在通信时、或是在将自己的结构传递给其他物质时需要符号呢？冯・诺依曼提出了第一个原因：任何能够组装自己物质部件的通用构造器，相比于通过物理上的自省（self-inspection）进行复制，用其物质部件的符号描述来复制会更加高效。尽管这听起来很有道理，但我没有找到强有力的物理证据或逻辑推理支持这种从效率出发的观点。无论如何，正如每个进化论者都会指出的那样，通过符号描述进行复制一定优于物理自省，因为这是自然选择的结果。冯・诺依曼暗示了第二个原因：更简洁的新描述更容易出现，而相对应的新物理结构则更难出现。这也不是一个普适的物理或逻辑论点，但从我们对分子遗传学和进化的了解来看，这也有道理。

考虑一个简单的物质结构，它可以通过一些物理过程进行自复制。假设该结构由 N 个部分组成，只要这些部分靠得足够近就能自我组装。那么问题来了，这个结构如何把正确的部分聚集在一起呢？给定一个零件储存库，最简单的方法是让结构的每个部分都具有个体遗传性，也就是说，每个部分都能从储存库中选择一个相似的零件。原则上，特殊折叠的大分子可以通过模板或特异性结合来实现这一点，一种带有多个部分的晶体化过程。然而，这种遗传过程没有开放式的演化潜力。首先，因为所有突变部分都必须具有这种固有的遗传特性，为了使这个过程实现开放式演化，我们必须假设遗传性质是大分子的一种相当普遍的固有性质。然而，事实并非如此。其次，通过模板识别的物质结构只能限于其外部部分，就像晶体生长一样。解决第一个限制的唯一已知方法是使用特殊的通用适配器，即一小组适配器就可以绑定任意数量的正确组件以及变异组件。摆脱第二个限制的唯一已知方法是展开内部。我们知道，分子适配器和折叠是所有细胞的一般策略，但实际上更加复杂。冯・诺伊曼没有讨论适配器的必要性，但从他的解决方案中可以清楚地看出，他认识到了假设一个可以适配自身的通用适配器的自指逻辑难题。正如我们在第 1 节中所概述的，他的解决方案基于形式图灵机在通用物质构造器中的普适性的逻辑要求。通常，通用机器是一种特定的适配器，可以指示其模仿任何机器的行为。逻辑上的要点是，要模仿另一台机器，必须有两个范畴上不同的指令级别。机器必须知道何时模仿，何时不模仿。换句话说，它必须区分虚拟机器和真实机器。 重要的是要理解，通用性仅适用于机器的可能的符号描述领域。换句话说，描述中可能接受突变，但是通用机器本身不太可能接受突变。这就是遗传密码的情况，它是巨大的开放式的各种蛋白质描述的通用阅读器。然而，物质部件和密码本身对于所有生物本质上是相同的。

图 9. 冯・诺伊曼的自复制自动机

10. 物质在演化与认知中的角色

如果逻辑可以在计算机等符号系统中实现，为什么特定的物质实体或硬件对于开放式演化如此重要呢？一开始，冯・诺依曼使用了蕴含物质 - 符号划分的动力学模型。而后，他转而使用没有这种划分的元胞自动机模型。尽管如此，他警告道：“通过这种方式公理化自动机，有一半的问题已经被忽略掉了，而这可能是更重要的那一半。” 毫无疑问，可编程计算机可以模拟生命、演化和认知活动的许多重要方面，这已经通过大量程序得到了清楚的证明。人工智能和人工生命领域有一个更强的主张，即计算机可以实现思维和生命。经验或逻辑无法推出这个结论，因为它们完全取决于一个人可以接受的抽象程度。如果我们同意把生命和思想抽象地定义出来，以至于排除足够多的物质因素，那么很明显，根据定义，一个有生命、能思考的计算机是可能的。同样地，如果我们同意将计算机的概念定义得足够广泛，以包括足够的物质方面，那么一切都可以称为计算。我认为追求这种不可判定的问题毫无价值。无论如何，一个只有符号或物质方面的片面模型，对于功能和语义问题，无法对给出令人满意的答案。

形式主义者常常忽略物理系统中一个不可避免的东西 —— 噪音，这与物理学家和生物学家的态度完全不同。噪音不仅在所有测量中不可避免，而且对于演化非常必要。计算机硬件和神经元也有噪音，但形式化模型却不蕴含噪音。通过良好的符号系统和硬件设计，符号操作时可以忽略噪音。对图灵测试评估机器能否思考的一个挑战是，观察机器是否会犯错误。当然，为了通过这个测试，可以在程序中引入随机误差。一个更有效、更困难的测试是不断在测试人员和机器中引入错误，并比较它们的学习或演化行为。

形式主义与功能主义关于计算和物质实现关系的观点

形式主义者和功能主义者认为，由于不同的物质硬件可以计算相同的函数，因此计算与其物质实现无关。但这仅在没有噪声、没有错误的符号操作的理想情况下成立。

形式等价计算对错误响应的差异

很容易看出，两个在形式上等价的计算，即计算相同函数的计算，通常会对错误产生完全不同的响应。即使在形式系统内也会出现这种情况。例如以下两个系统：

• 系统一：以规则 $0\to 1$ 和 $1\to 01$ 重写产生比特序列。
• 系统二：从 $S_0=0$ 和 $S_1=1$ 开始，按照 $S_{n+1}\to S_{n-1}\circ S_n$ 的规则进行递归（译者注：这里的 $S_{n-1}\circ S_n$ 是将两个字符串按顺序拼接起来，即 $0\circ 1=01$）。

这两个系统输出的结果是完全相同的。但是，只要在字符串中的任何位置出现了错误，就将生成完全不同的字符串。如果实现计算的物质结构也有噪声，这个问题只会变得更加严重。

突变测试的作用

这种突变测试可以用来发现两个在形式上等价的计算是否使用了不同的硬件、架构或程序来实现。例如，连接机器、元胞自动机或任何数量的机器可能在形式上是等价的，但它们对硬件或软件中的噪声的响应不可能高度相似，或能够被预测。

形式主义者和功能主义者认为，由于不同的物质硬件可以计算相同的函数，因此计算与其物质实现无关。但这仅在没有噪声、没有错误的符号操作的理想情况下成立。然而，很容易看出，两个在形式上等价的计算，即计算相同函数的计算，通常会对错误产生完全不同的响应。即使在形式系统内也会出现这种情况。
例如这两个系统：其中一个以规则 $0\to 1$ 和 $1\to 01$ 重写产生比特序列；另一个则从 $S_0=0$ 和 $S_1=1$ 开始，按照 $S_{n+1}\to S_{n-1}\circ S_n$ 的规则进行递归（译者注：这里的 $S_{n-1}\circ S_n$ 是将两个字符串按顺序拼接起来，即 $0\circ 1=01$)。这两个系统输出的结果是完全相同的。但是，只要在字符串中的任何位置出现了错误，就将生成完全不同的字符串。如果实现计算的物质结构也有噪声，这个问题只会变得更加严重。这种突变测试可以用来发现两个在形式上等价的计算是否使用了不同的硬件、架构或程序来实现。例如，连接机器、元胞自动机或任何数量的机器可能在形式上是等价的，但它们对硬件或软件中的噪声的响应不可能高度相似，或能够被预测。

模型 1（无噪声）：0，1，01，101，01101，10101101…

模型 2（无噪声）：0，1，01，101，01101，10101101…

模型 1（有噪声）：0，1，11，0101，101101，0110101101…

模型 2（有噪声）：0，1，11，111，11111，11111111…

这显然是一种非常通用的测试，因为实际上，当噪声与可遗传记忆和自然选择相结合时，噪声就是演化本身的基础。功能主义者认为同一功能可以由多种物质结构实现。这样的立场应该通过另外三个物理和生物事实来予以反驳。首先，同一物质结构可以执行不同的功能，因为功能不是任何结构的内在属性。第二，给定的物质结构的潜在功能的范围和质量将取决于该物质结构的细节。也就是说，两个不同物质结构不会具有完全相同的潜在可演化功能的范围。一般来说，不同的物质结构将以不同的方式演化，即使它们曾经同时具有相同的功能。第三，有效的演化搜索取决于符号空间如何映射到物质功能。蛋白质的三维折叠不仅仅与一维基因序列（只有符号规则的）相关联，更关键的是取决于物质结构和物理定律。

和在生物体演化中大脑的作用相比，实现认知活动的脑部物质结构的作用并没有被深入理解。功能主义者和计算主义者仍然使用同样的论点，即大脑的符号行为不依赖于物质实现。如果认知行为远离其物质依赖的基础（如感觉运动控制），被抽象得足够高，那么这根据定义而言是正确的。然而，刚刚提到的三个事实也适用于大脑的演化和学习过程。因此，若不依赖于物质上的感觉运动结构，快速准确分类过程（比如复杂的视觉模式识别）是不太可能成功演化的。

11. 结论

如我在第 1 节中所示，我要求生命理论在认识论上不仅要与逻辑一致，还要与基本物理原理一致。最基本的认识论分类是 “不变的事物” 和 “变化的事物” 之分。在物理学中，这个原则被用来定义物理定律和初始条件。这意味着 “自指无能原理”（ self-referent impotency principle），即不变的事件不能完全描述变化的事件。也就是说，物理定律无法完全描述测量结果。更确切地说，测量所需的分类函数无法从物理定律中导出。否则，物理定律可以通过计算推导出它们自己的初始条件。在形式系统中，相应的自指无能原则是它们无法证明自己的一致性，更不能为自己的公理赋予真值。这意味着形式符号系统也无法进行测量。符号计算永远无法实现测量。

物理定律和自然选择是事件的互补模型。物理定律描述了有机体无法控制的事件。自然选择是一种关于有机体如何增加对事件的控制的理论。我所说的自然选择是指通过符号指令的遗传变异，来修改对群体相对生存率分布的新达尔文演化过程。这种修改进行于很多组织层面上（例如，Sober，1984）。我们可以将非选择性自组织（nonselective self-organization）定义为：在不受符号指令约束的系统中，由现有或未来的物理定律产生的秩序。

Kauffman（1993）在他对非选择性排序过程的探索中指出，没有一个既定的研究领域将非选择性物理秩序纳入演化理论。在某种程度上，这可能是科学模型中的另一个文化偏见案例，源自经典物理学家对物质和符号的分类。另一个原因可能是，我们直到最近都缺乏一个与生物体有关的物理自组织理论。但现在不一样了。正如我在第 8 节提到的，现在复杂物理系统有很多发现，这些系统展现出了一种类似于生命的涌现秩序。但是，在这些研究中很少涉及物质 - 符号划分。只有关于基因密码起源的理论似乎与物质 - 符号划分直接相关（例如，Bedian，1982）。就像人工智能的情况一样，涌现演化的计算模型研究紧紧围绕经典的物质 - 符号问题展开，但很少探讨这种区分的物理基础，以及物质和符号是如何通过测量相互关联的。

基于以上种种原因，我认为研究生命、演化和认知理论的一个有效方法是，必须关注这两者的互补贡献：其一是非选择性的，基于物理法则的物质自组织；其二则是基于自然选择的符号组织。希望这是一个可以经验验证的问题，尽管肯定极其困难。也许更好的表述方式不是关于物质和符号方面的贡献，而是关于这两个方面如何相关，这种关系本身如何产生，以及如我用语义闭包所暗示的，为什么这种物质 - 符号互补性对于演化越来越复杂的组织、越来越复杂的思想和模型是必要的。

参考文献

Bedian, V., 1982, The possible role of assignment catalysts in the origin of the genetic code, Origins of Life 12, 181.

Born, M., 1965, Symbol and reality, Universitas 7, 337-353. Reprinted in Born, M., Physics in my Generation, Springer-Verlag, NY, pp. 132-146.

Burgers, J. M., 1963, On the emergence of patterns of order, Bull. Am. Math. Soc. 69, 1-25.

Cassirer, E., 1957, The Philosophy of Symbolic Forms, Vol 3: The Phenomena of Knowledge, Yale Univ. Press, New Haven, CT.

Churchland, P. M., 1981, Eliminative materialism and the propositional attitudes, Journal of Philosophy, vol. LXXVIII, no. 2.

Churchland, P. M., 1984, Matter and Consciousness, MIT Press, Cambridge, MA. Crick, F., 1993, The Astonishing Hypothesis, Scribner’s Sons, NY.

Glansdorff, P. and Prigogine, I., 1971, Thermodynamics of Structure, Stability, and Fluctuations, Wiley, London.

Haken, H., 1977, Synergetics, Springer, Berlin.

Harnad, S., 1990, The symbol grounding problem, Physica D 42, 335-346.

Hertz, H., 1894, The Principles of Mechanics, Introduction. Quoted from H. Weyl, Philosophy of Mathematics and Natural Science, Princeton Univ. Press, Princeton, NJ(1942), p. 162.

Houtappel, R. M. F., Van Dam, H., and Wigner, E. P., 1965, The conceptual basis and use of the geometric invariance principles, Rev. Mod. Physics 37, 595-632.

Jen, E., 1989(ed) Lectures in Complex Systems. Addison-Wesley. Redwood City, CA.

Kauffman, S. A., 1969, Metabolic stability and epigenesis in randomly connected nets, J. Theoretical Biology 22, 437.

Kauffman, S. A., 1993, The Origins of Order, Oxford Univ. Press.

Langton, C., 1988, Artificial Life, Addison-Wesley, Redwood City, CA.

Langton, C., 1992, Introduction. In Artificial Life II, C. Langton, C. Taylor, J. Farmer, and S. Rasmussen, Eds., Addison-Wesley, Redwood City, CA, pp. 1-23.

Leff, H. S. and Rex, A. F., Eds., 1990, Maxwell’s Demon, Entropy, Information, Computing, Princeton Univ. Press, Princeton, NJ.

Newell, A., 1980, Physical symbol systems, Cognitive Science 4, 135-183.

Nicolis, G. and Prigogine, I., 1977, Self-organization in Non-equilibrium Systems, Wiley, NY.

Nicolis, G. and Prigogine, I., 1989, Exploring Complexity, Freeman, NY.

Pattee, H. H., 1969, How does a molecule become a message? Developmental Biology Supplement 3, 1-16.

Pattee, H. H., 1972, Laws, constraints, symbols, and languages. In Towards a Theoretical Biology 4, C. H. Waddington, Ed., Edinburgh Univ. Press, pp. 248-258.

Pattee, H. H., 1982, Cell psychology: An evolutionary approach to the symbol-matter problem. Cognition and Brain Theory 5(4), 325-341.

Pattee, H. H., 1988, Simulations, realizations, and theories of life. In Artificial Life, C. Langton, Ed., Addison-Wesley, Redwood City, CA, pp. 63-77.

Pattee, H. H., 1990, Response to E. Dietrich’s “Computationalism,” Social Epistemology 4(2), 176-181.

Pattee, H. H., 1992, Emergence in physical, computational, and network models. In Complex Adaptive systems and Evolution of Information, M. J. Patel and I. Harvey, Eds., in press.

Post. E., 1965, Quoted from M. Davis, Ed., The Undecidable, Rowen Press, Hewlett, NY.

Pylyshyn, Z., 1984, Cognition and Computation, MIT Press, Cambridge, MA.

Rosen, R., 1977, Complexity and system description. In Systems, Approaches, Theories, Applications, W. E. Harnett, Ed., D. Reidel, Boston, MA.

Simon, H. A.(1962) The architecture of complexity, Proc. Am. Philos. Soc. 106, 467- 482.

Sober, E., 1984, The Nature of Selection, MIT Press, Cambridge, MA.

Stein, D.L., 1988(ed) Lectures in the Sciences of Complexity. Addison-Wesley, Redwood City, CA.

Stein, D.L. and Nadel, L.(eds) Lectures in Complex Systems. Addison-Wesley. Redwood City, CA.

Toffoli, T.(1982) Physics and computation, International J. of Theoretical Physics 21, 165-175.

Thomson, D., 1942, On Growth and Form, 2nd Ed., Cambridge Univ. Press.

von Neumann, J., 1955, Mathematical Foundations of Quantum Mechanics, Princeton Univ. Press, Princeton, NJ, Chapter VI.

von Neumann, J., 1966, The Theory of Self-reproducing Automata, A. Burks, ed., Univ. of Illinois Press, Urbana, IL.

Waldrop, M. M., 1992, Complexity, Simon & Schuster, NY.

Weber, B. H., Depew, D. J., and Smith, J. D., 1988, Entropy, Information, and Evolution, MIT Press, Cambridge, MA.

Wheeler, J. and Zurek, W., 1983, Quantum Theory and Measurement, Princeton univ. Press, Princeton, NJ.

Wheeler, J. A., 1990, Information, physics, quantum: The search for links. In Complexity, Entropy, and the Physics of Information, W. H. Zurek, Ed., AddisonWesley, Redwood City, CA.

Whitehead, A. N., 1927, Symbolism: Its meaning and Effect, Macmillan, NY.

Wigner, E. P., 1964, Events, laws, and invariance principles, Science 145, 995-999.

Yates, F. E., 1987, Self-organizingSystems: The Emergence of Order, Plenum, NY.

Yovits, M. C. and Cameron, S., Eds., 1960, Self Organizing Systems, Pergammon, NY.

Yovits, M. C., Jacobi, G. T., and Goldstein, G. D., Eds., 1962, Self Organizing Systems, 1962, Spartan, Washington, DC.

Zurek, W.H., 1990(ed), Complexity, Entropy, and the Physics of Information., Addison-Wesley, Redwood City, CA.

---

大模型向通用意识机器进化的关键 —— 自指的启示

张江 集智俱乐部 2025 年 02 月 12 日 19:03 上海

导语

自指（self reference）不仅可以构造悖论，导致图灵停机问题和哥德尔不完备性定理，同时也是生命自复制和意识机器最核心的部分。我们猜测，未来 ChatGPT 朝向通用意识机器进化，其中关键就是实现一个 Quine 结构。同时，随着类 ChatGPT 等 AIGC 内容的泛滥，人和机器的互动将陷入一种 “图灵游戏” 的模式，这种模式可以用于说明图灵停机问题的不可能性，也可以用于人机博弈 —— 机器用一定规则产生内容，用户识别出这种规则，从而逼迫机器进入更深层次的规则创造。不断递归这种模式，机器将内在虚拟层不断深化，最终可能导致智能爆炸……

ChatGPT 的一个研究方向就是让机器具备一定的自指能力，如自我提高（self improve），自我下命令（self instruction）。

关键词：自指，递归定理，自复制自动机理论，生命自复制

张江 | 作者

1. 自指 —— 一条永恒的金带

自指是一个非常古老的话题，它通常与古代奥义以及各种神秘哲学有关。例如佛教中所提倡的 “观身无常、观心无我”，以及古希腊的 “认识你自己”，都在劝解人们能够将心智的观察箭头指向自己。中国道家所倡导的 “无”，正是一个最简单的一字悖论。

自噬的蛇

一幅最能体现自指深邃含义的图画莫过于这条正在吞噬自己的蛇。此蛇作为一种图腾曾广泛出现在北欧神话、基督教神学、印度教和非洲宗教之中。这条蛇将自指那种深刻的自我毁灭性体现得淋漓尽致 —— 我们可以想象一下当它把自己吞噬完毕会产生怎样怪异的情景。

将这种自我毁灭性的古代奥义应用到现代科学中已经产生了一系列深刻的结论。 首先，在 19 世纪末，著名数学家康托尔（George Cantor）将 “对角线删除” 法则应用到集合论中，从而证明了实数的个数比自然数多。紧接着，罗素（Bertrand Russell）提出了著名的 “罗素悖论” 而摧毁了弗雷格（Gottlob Frege）的数学大厦。年仅 25 岁的哥德尔（Kurt Gödel）巧妙地应用同样的破坏性自指一举摧毁了数学大师希尔伯特（David Hilbert）的完备一致性的数学体系梦想。图灵（Alan Turing）则利用同样的技巧进一步发现任何超级计算机都不可能求解的图灵停机问题。

《纽约时报》曾将哥德尔不完备定理评价为 20 世纪最伟大的数学定理。自指可以用来构造破坏性的悖论已经是众人皆知、司空见惯了。然而，这种认识其实很片面。自指包含了比自指悖论更宽泛的内容，因为在自指大家庭中，还包括另外一类构建性的成员。

1953 年，正当人们举杯欢庆沃森和克里克发现了 DNA 双螺旋结构，并从分子层面上解释了生命的自我复制之谜的时候，另外一名伟大的美国匈牙利裔数学家：约翰・冯・诺依曼（John von Neumann）正在独立地思考着生命自我复制的逻辑基础。然而，令人遗憾的是，那时的冯诺依曼已经患上了癌症，并于 1957 年的 2 月去世。于是，他的助手阿瑟・伯克斯（Arthur Burks）将他关于自复制自动机的理论整理成书《Theory of Self-reproducing Automata》，并于 1966 年出版。

与沃森・克里克不同的是，冯诺依曼要寻找的是生命自我复制的逻辑基础而非物质基础。虽然冯诺依曼没有明确指出，但是已经暗含了这个自复制的逻辑基础不是别的，正是一种自指结构。也就是说，**自指恰恰是生命实现自我复制的逻辑内核。**这也许会让读者感到困惑。不是说，自指都是用来构造诸如哥德尔定理、罗素悖论之类的破坏性武器吗？实际上，还存在着另外一大类自指，笔者称之为 “建构性的自指”，它不但不会引起破坏，反而能够创造很多令人意想不到的惊奇结构。至于自我繁殖的系统是如何令人意想不到的，请参考第 4 节的讨论。

实际上，早在 1938 年，与哥德尔共同奠定递归函数论基础的数学家克林尼（Stephen Kleene）就证明了递归函数论中的一个著名定理：递归定理（更精确地说，应该叫 Kleene 第二递归定理）。根据它，人们可以很轻松地得到一个数学推论，系统的自我复制是可能的。

证明递归定理的核心技巧，是一个被称为 “蒯（kuai3）恩” 的特别技术。 蒯恩（Willard.V. Quine）是美国的哲学家，终身致力于哲学、数理逻辑、集合论的研究。他创造了一种称之为蒯恩的方法，使得人们可以不通过使用 “我” 或者 “这句话” 等词语就能创造出可以谈论自身的句子来。

有趣的是，蒯恩构造恰恰就是那条 “黄金对角线”（这一方法正是当年康托尔最早提出证明实数比自然数多的方法，也是哥德尔定理构造哥德尔句子的关键技术）。只不过，康托尔、哥德尔等人的对角线与蒯恩的对角线方法稍有不同。我们会在第 6 节中详细地讨论这些技术。

总而言之，从宗教到科学，从悖论到自复制，自指是贯穿始终的主题。正如《哥德尔、艾舍尔、巴赫》这本书指出的那样，自指是一条永恒的金带。

2. 语言中的自指

提到自指，很多读者马上就会联系到那句臭名昭著的悖论句子：

这句话是错的

这句话之所以让人讨厌，是因为你无论从正面（即假设它是对的），还是从反面（即假设它是错的），都会得出相反的结论。因此，这句话既不对也不错。

然而，这句 “说谎者悖论” 仅仅是广大自指语句家庭中的成员之一，有很多语言是自指的，但却是无害的甚至是有益的。比如下面的句子：

这句话是对的

这句话就是一个既可以是对又可以是错的句子。你可以非常虔诚地承认这句话所论述的内容是对的，然后，再看它的内容，它正在陈述：它自己是对的。于是你初期的假设被证实了。另一方面，当你假设它是错误的时候，你就会知道它的语义 “这句话对” 是错误的，于是你就真的得到了这句话就是错误的结论。也就是说这句话的对错完全取决于你的假设。

当然，还有一些更好玩的自指句子，如：

这句话有 2 个‘这’字，2 个‘句’字，2 个‘话’字，2 个‘有’字，7 个‘2’字，11 个‘个’字，11 个‘字’字，2 个‘7’字，3 个‘11’字，2 个‘3’字

这被称为自描述语句，也就是说这个句子正在描述自己的 “分子” 构成。当你尝试独立写下这样一个自描述语句的时候就会发现，你其实并没有创造这句话，而是这句话正在 “迫使” 你写出它自己。这是因为，按照这个句子的逻辑一旦你开始写下第一个字，你就必须按照已出现的字的情况而自动补全后面的句子。同时，这个语句还具有了不起的自我修复性。你不妨将该句子中的某一个汉字删掉（例如你删除第一个‘2’字），就会很快发现该句子中的一部分出现问题了，即 “7 个‘2’字” 是错误的。因此，你会根据句子整体的意思指导而发现你少了一个‘2’字。

因此，自指不都是破坏性的，更多的自指是无害的，而且可以给我们带来一定的 “惊奇性”。这种惊奇性的来源主要是自指语句中包含的无穷递归，因为它可以创造无限的虚拟层次。

虚拟层次是一个我们司空见惯的概念，例如故事中的故事，电影中的电影，梦境中的梦境等等（电影《盗梦空间》（Inception）就是对梦中梦层次的一个非常好的展示）。在上一章中，我们已经领略了程序是可以通过模拟而产生多个虚拟层次的。在语言中，我们不妨将引号看作是标识一个新的虚拟层次出现的符号。这样，下面这句话：

“明天会下雨” 是错的

就包含了两个层次，更深一层的句子是 “明天会下雨”，而上面一层则是 “‘明天会下雨’是错的”。当然，我们通过不断地加引号就能创造出各种复杂的嵌套结构。

另外，人们发明了一类代词可以指代不同的句子。例如 “这句话”，“那句话”。这些代词就仿佛是一个指针会将一个句子整体放到一个引号中而实现多个层次的嵌套。例如下面两句话：

下面的句子是对的

明天会下雨

在第一句话中出现了一个指代词 “下面的句子”，它是一个指针指向了 “明天会下雨” 这句话，于是我们观察者作为一个解读器就会将这两句话解释为：

“明天会下雨” 是对的

也就是说，我们照指代词的意思将 “明天会下雨” 这句话加上了引号放到了第一句中的 “下面的句子” 那个指代词之中了。于是，指代词创造了包含了两个虚拟层次的句子。

按照同样的逻辑，当我们遇到了指代词 “这句话” 的时候会发生什么呢？我们将会得到一个包含无穷虚拟层次的语句。例如我们将自指语句 “这句话是错的” 按照代词的法则展开就会得到：

““““…………” 是错的” 是错的”…………” 是错的” 是错的

我们看到，只要 “这句话” 这个指代词一出现，我们就能够得到无穷。因此，自指语句往往都与无穷虚拟层次有关。注意，我这里用的词语是 “往往”，而不是 “一定”。之所以这样说，是因为的确存在着一种构造自指语句的方法，让我们绕过无穷。这种方法就是大名鼎鼎的蒯恩法。

在讨论蒯恩之前，让我们先来领教句子中的动词（动词短语）。大部分动词是与我们读句子的观察者无关的，例如：

小明起床了

这个句子表达了小明这个人物正在做的一个动作是起床了。其中 “起床了” 就是一个动词。当然，有很多动词不仅可以描述一个人或者事物，还可以去描述句子，例如：

“小明起床了” 包含 5 个字

这里面的 “包含 5 个字” 就是一个描述句子 “小明起床了” 的动词。还有一些句子包含了动词，而这个动词是使役我们读这个句子的观察者做出某种动作的：

删除 “小明起床了” 中的第一个字

这个 “删除第一个字” 的动作就是使役读句子的观察者做出的，于是，我们按照这个句子的说法进行操作，就会得到一个新句子：

明起床了

我们可以再做稍微复杂一点的操作，例如：

把 “小明起床了” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

按照这个句子所描述的复杂操作（你最好拿来一个草稿纸，自己在纸上写一写），我们就可以得到：

小 “小明起床了” 明起床了

好，既然你已经熟悉了这个复杂的操作，那么让我们来看下面一个古怪的句子：

把 “把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

如果按照这个句子指示的操作你会得到什么？让我们来做一做。按照这个句子的要求，我们可以把引号之中的句子施行下面的三步操作：第一步，把第一个字，也就是 “把” 放在左引号前面，这样就得到的新句子中的第一个字：“把”；第二步，将后面的字放在右引号后面，这样新句子就会以 “中的第一个字放到…… 字不变” 为结尾；第三步，保持引号和其中的字不变，于是新句子的中间会有一个引号，并且引号的中间就会是 “把中的第一个字放到……”。于是，我们得到的新句子就是：

把 “把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

请注意，这个新句子和原句子是一模一样的！事实上，原句子使役我们观察者完成了一次对自己的拷贝！这个句子其实就是大名鼎鼎的蒯恩了！

也许，你已经有些糊涂了，让我们再好好看看究竟蒯恩是怎么操作的。首先，我们定义了一种具有动词的句子，也就是：

把 “X” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

我们不妨将这个句子记为 $Q\left(X\right)$，其中的 $X$ 就是一个空穴，可以往其中添放任何一个句子。例如，如果我们让 $X$ =“小明起床了”，那么原句子 $Q\left(X\right)$ 就成为了一个完整的句子：

把 “小明起床了” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

按照 $Q\left(X\right)$ 的意思对 $X$ 进行操作就得到了新句子 $Y$ ：

小 “小明起床了” 明起床了

在这个例子中，$Q\left(X\right)$ 显然与 $Y$ 没有什么关系。

进一步，如果去除句子 $Q\left(X\right)$ 中的空穴 $X$，我们可以得到：

把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

它也是一个句子（尽管它不完整），我们记它为 $Q$。最关键的时刻来临了：我们让 $X=Q$ 并代入 $Q\left(X\right)$ 之中会怎样？也就是将除去空穴的句子部分 $Q$ 放到 $Q\left(X\right)$ 这个句子的空穴 $X$ 之中：

把 “把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

我们不妨把这个句子记做 $Q\left(Q\right)$，因为我们把空穴 $X$ 换成了残句子 $Q$ 。之后，我们再按照这个句子所给出的使役动词进行操作，就能得到新句子 $Y$，也就是：

把 “把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

令人惊奇的是，经过动词操作之后创造的句子$Y$ 与原来的句子 $Q\left(Q\right)$ 竟然是一模一样的！所以句子 $Q\left(Q\right)$ 利用使役动词完成了 “自复制” 过程，也就是 $Q\left(Q\right)=Q\left(Q\right)$ 。

我们把这种技巧称之为蒯恩以纪念它的发现者美国哲学家 W.V. Quine。你会看到，这种技巧可以让我们不用 “这句话” 指代词就能够造出自指语句，比如下面这个句子：

把 “把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变得到的句子是假的” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变得到的句子是假的

注意，这个句子与前面的句子稍有不同，这就是在后面加上了一个判断 “得到的句子是假的”。我们不妨记 $F=$
得到的句子是假的”，并且把：把 “X” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变得到的句子是假的

这句话记为 ，其中 符号表示将两个句子粘合在一起形成新的句子，于是 就是：

把 “把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变得到的句子是假的” 中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变得到的句子是假的

我们可以验证，经过 句子所描述的操作之后得到的句子跟 是一模一样的。所以这句话就相当于：“这句话是假的”。我们没使用 “这句话” 指代词就实现了自指。

有关更多的语言中的蒯恩操作的讨论请参看《哥德尔、艾舍尔、巴赫 —— 集异璧之大成》一书的对话《G 弦上的咏叹调》，以及《Diagonalization and Self-Reference》一书。

也许你会觉得我们在玩弄语言游戏，然而，这种语言技术却在数学和计算机中起到了非常大的作用，因为蒯恩句子恰恰就是自复制机器的逻辑基础，也是 Godel 定理证明过程中的关键一步。 下面，我们分别对建构性自指和破坏性自指进行详细地介绍。

3. 建构性的自指

虽然提起自指，人们很容易想到自指悖轮。但是，人们不熟悉的是另外一大类无害的自指，它们通常直接应用蒯恩技术，而实现某些意想不到的结构或者功能。下面，让我们先从一种最简单的建构性自指：自打印程序说起。

所谓的程序自打印就是指一个程序能够在不读取外部文件的条件下把自己的源代码打印出来。 首先，我们要先领教一下，一个自我打印的程序是多么不可能的！我们知道，要写一个程序打印出 “helloworld!” 字样是非常容易的，例如：

Print(‘helloworld!’)

注意在这个程序中，字符串都用单引号括起来。那么，我们能不能写一个程序，把这个打印 “helloworld!” 程序的源代码打印出来呢？这也是可以办到的，例如下面的程序：

Print(‘Print(\’helloworld!\’)’)

注意，这里面的 “\’” 会被编译器解释为一个字符串，这个字符串中就有一个字符：“ ` ”。采用这个技巧，我们就可以解决如何在一个引号之中再输入一个引号的问题了。所以，我们可以很轻松地打印出这个能够打印”helloworld!” 程序的程序源代码出来。但是很显然这个程序并不能打印出它自己，也许你会想到能不能打印出上面的程序源代码出来？当然可以！

Print(‘Print(\’Print(\\\’helloworld!\\\’)\’)’)

其中 \ 就表示包含一个字符 “\” 的字符串变量，这样 Print(‘\’) 就会打印出一个字符 “\”，而 Print(‘\\’’) 就会打印出字符串 “\’” 出来。所以，引号里面可以放入任意层次的引号。

但是这个程序仍然不能打印自己！你很快发现，我们人类是写不出这种能够打印自己的程序的，因为它包含了无穷递归。不过，通过蒯恩技巧，实际上我们完全可以写出来一个自打印程序，如下：

S(x){ q=’S(x){\\n q=\\\’\’+q+\’\\\’;\\n
Print(\\\’\’+p(q)+\’\\\’);\\n}’;
Print(‘S(x){\n q=\’’+q+’\’;\n Print(\’’+p(q)+’\’);\n}’); }

源代码 1：自打印程序源代码

这里面的 “\n” 表示换行符，即如果执行 Print(‘A\nB’)，则程序会输出下面的字符串：

A
B

“+” 表示将两个字符串进行串联形成一个新的字符串，例如 A=’123’,B=’456’，则 A+B=’123456’。

**这个自打印程序调用了一个简单的解码函数 $p\left(q\right)$， $p$ 的作用是将字符串 $q$ 变换成更浅一层次的字符串。**例如，如果 $q$ 是 “\\’\’\n\”，那么 $p$ 这个函数就会计算输出 “\’’\n\”。也就是说 $p$ 完成了一组映射：它把 “\” 映射成 “\”，把 “\’” 映射成 “’”，而把 “\n” 映射成回车符。显然 $p$ 是可以写出来的。我们知道，由引号的引用可以形成更加深层次的虚拟世界（参见上一小节）。所以 $p\left(q\right)$ 的作用就是让字符串 $q$ 弹出一层虚拟世界。由于$p$ 的作用很简单，我们假设它是一个系统自带的函数，因此就不在源代码 1 中给出 $p$ 的实现代码了。

S(x) 这个程序中包含了过多的 “\” 和 “’” 符号，这就导致我们理解源代码 1 稍显困难，下面我们将把该程序表示成下面的图，从而让读者看得更清晰一些：

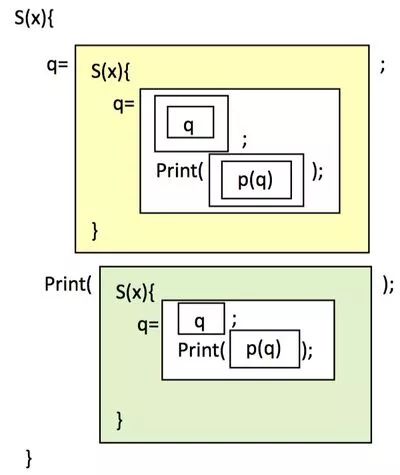
自打印程序源代码中的引号层次示意

如上图，这个自打印程序中的引号全部用方框来替代。这样第一层引号’…’就对应了第一层的方框，引号中的引号，即 “\’…\’” 就对应了框中的一个框。这样，由于程序中出现最多的层次是四层引号，即 “\\’”，所以上图中就出现了第四层框。

另外，我们还观察到，这个程序包含了两个大框，即 “q=” 后面的黄框和 “Print()” 之中的那个蓝框。这两个框的结构是完全一样的，只不过黄框比蓝框多了一个虚拟层次，这反映在所有的蓝色框中的最深一层框都再加上一层框就得到了黄色框。

更有趣的是，整个程序 S(x) 实际上和这两个框是相似的，因此这个程序本身就是一个分形结构。在传统的分形结构中，每一个部分都会包括无穷多的细节。但是，在这个自打印程序中，虽然有嵌套的分形结构，但是却没有达到无穷，最深的引号也仅仅有 4 层。

让我们来分析一下这个程序是如何运作的。首先，看程序的最后一行，即 Print(‘S(x){\nq=\’’+q+’\’;\nPrint(\’’+p(q)+’\’);\n}’); 这句话的作用是让程序在屏幕上打印出一个字符串。注意观察，这个被打印出的字符串其实是由 “+” 号被分割成了 5 个部分，第一部分是 “S(x){\nq=\’”，第二个部分是 $q$ 这个字符串的原封不动的拷贝，第三部分是字符串：“\’;\nPrint(\’”，第四部分是函数 $p$ 作用到 $q$ 上面的结果即 $p\left(q\right)$；第五部分还是一个字符串：“\’);\n}”。然后当我们把 q 字符串的数值代入第二部分和第四部分，并进行运算 $p$ 之后，就得到了和源程序一模一样的结果。你不妨在计算机上运行这段程序，就会发现这段程序会在屏幕上赤裸裸地把自己的源代码打印出来。

我们不妨把这段程序的 5 个部分进行归并，写成由下面的三部分构成的：，其中 Copy 就是 5 部分中的第二部分，即相当于一个拷贝字符串的程序，你输入 给 Copy 什么字符串，Copy 就会把那个字符串再原封不动地吐出来；Popup 这部分就是原来的 5 部分中的第四部分，即函数 $p$，它的作用相当于一个弹出操作，也就是为输入的字符 串脱去一层引号。如果输入的字符串原来是在第 $n$ 层虚拟世界，则 Popup 的作用就是让字符串跳到第 $n-1$ 层；最后 Control 这部分就相当于原来的第 1、3、5 这三部分以及最一开始的语句 Print 的总合，它的作用就相当于是为 Copy 和 Popup 制造出来的字符添加适当的连接词，使得最后的字符串能够拼接成与原来的程序一模一样的源程序，并将其打印到屏幕上。所以这句 “Print(‘S(x){\nq=\’’+q+’\’;\nPrint(\’’+p(q)+’\’);\n}’);” 就可以改写成。其中 “о” 表示将不同的程序连接为一体。

如果我们把一个计算机程序 $X$ 的描述（或者称源代码）写为 $\lambda \left(X\right)$ ，则自打印程序的第一条赋值语句就相当于给 $q$赋予了 ，即 这三个程序连在一起的源代码。最后我们可以将自打印程序简写为：

S(x){
q= λ(Copyo Popupo Control)
(Copyo Popupo Control)(q); }

源代码 2：自打印程序的源码缩写

我们可以进一步地把它简写为：$Q\left(q\right)$，其中 $Q$ 表示 这三个程序的联合程序，而 $q$ 则表示联合程序的源代码。$Q\left(x\right)$ 这个程序的作用是输出一个特殊的字符串 $X\left(x\right)$ 即程序 $X$ 调用自己的代码 $x$ 的源程序，我们称这个 $Q$ 为蒯恩函数。

那么，自打印程序不是别的，正是将蒯恩函数 $Q$ 自己的源代码再喂给它自己，这样就产生了 $Q\left(q\right)=Q\left(q\right)$ 的效果。 等式左边是 $Q$ 对 $q$ 的计算，是一个动作，它的结果产生了等式右边的字符串 $Q\left(x\right)$ ，而这个字符串恰恰就是 $Q$ 作用于 $q$ 的源代码。我们看到，第 2 节中的蒯恩方法与这里 的 $Q\left(x\right)$ 是一模一样的。仔细想想不难发现，其实自打印程序的逻辑与蒯恩语句的逻辑是相通的。因此，自指恰恰就隐藏在了这段自打印程序之中了。

我们只要对这个自打印程序稍加更改就能创造出自我复制的程序出来。首先，我们要说明程序的自我复制究竟是什么意思。假设内存中漂浮着很多大大小小的程序，某一个程序 $P$ 能够自我复制是指，当 CPU 执行到程序 $P$ 的时候，$p$ 就会命令 CPU 执行一系列的操作使得它自己的一份拷贝会出现在内存中。但是，需要强调的是 $P$ 不能够从硬盘上读取文件，否则自我复制将变得异常简单，只要把硬盘上的源程序再调用到内存中就行了。乍一看，这似乎与自打印程序一样不可能实现。但是利用与自打印程序同样的蒯恩技巧，我们依然可以很轻松地构造出自复制的程序出来。

我们只需要把自打印程序 中的 改成 Construct 就可以了。这里的 Construct 是一个函数，你输入给 Construct 一段程序的源代码 $x$，它就能把 $x$ 所对应的程序 $X$ 编译出来并驻留在内存中。这样，程序 就可以完成自复制功能。

进一步，利用同样的逻辑，我们也能够制造出可以复制自身的真实机器。只要让 Construct 代表从给定机器的描述 $\lambda \left(X\right)$ 而构造出实际机器 $X$ 就行了。在冯诺依曼的著作《自复制自动机理论（Theory of Self-reproducing Automata）》一书中，作者试图构建的自复制自动机就包括了这四个部分。即自复制机器是由一个通用拷贝机（Copy）、一个通用构造机（Construct）和一个控制器（Control）以及所有这三台机器的描述即源代码 构成的。

在此小节中，我们用自打印程序和自复制程序为例来说明了建构型的自指。然而，建构性的自指实际上不仅仅是这两种，它还会有各种各样的用途。

全文请参看：

[1] 集智百科：系统中的观察者(5)——自指
https://wiki.swarma.org/index.php/系统中的观察者(5)——自指

以及更多的参考书，包括：侯世达：《哥德尔、艾舍尔、巴赫》，商务印书馆，1996；R.M. Smullyan: Diagonalization and Self-Reference,Oxford University Press, 1994。

延伸阅读论文：

• Large Language Models Can Self-improve | OpenReview
  Published: 01 Feb 2023, Last Modified: 13 Feb 2023Submitted to ICLR 2023
  https://openreview.net/forum?id=NiEtU7blzN

• Self-Instruct: Aligning Language Model with Self Generated Instructions
  https://arxiv.org/abs/2212.10560

---

via:

• 自指丨自指是什么？
  https://mp.weixin.qq.com/s/9SY2JP0Q4g4bGYDweit2RQ

• 自指太特殊了
  https://mp.weixin.qq.com/s/Okdc4TIQE8cXNZ73ZLO2Lw

• 研究自指的最好方法是自指本身
  https://mp.weixin.qq.com/s/YUMjWWWJqd94Y7LRS2BOUw

• 什么是自指 | 集智百科
  https://mp.weixin.qq.com/s/fQqJ106erMfuW2VbMhlIYA

• 自指机器的奥秘
  https://mp.weixin.qq.com/s/byloeXGCC0luwooO6uYWYQ

• 自指的演化：物质、符号和语义闭包
  https://mp.weixin.qq.com/s/NayP8cqa_4oGPMFsdjF1Eg

• 大模型向通用意识机器进化的关键 —— 自指的启示
  https://mp.weixin.qq.com/s/jBZwi83nLjU68HlPb0u1qQ