深入浅出搞懂VAE

2013年提出的VAE，跨越11年，获得首届ICLR‘24时间检验奖，是深度学习的重要技术之一。

原文：https://arxiv.org/pdf/1312.6114 

---

这篇论文把深度学习和可扩展的概率推理整合在一起，从而产生了变分自编码器（VAE），这项工作其持久的价值在于优雅，加深了我们对于深度学习和概率建模之间相互作用的理解，引发了许多后续有趣的概率模型和编码方法的开发。

下面按照三个部分进行，由易到难：核心思想，技术难点和实现（如何将概率转换成网络？），理论支持（变分下界推导，损失函数），复盘

0. Variational Auto-Encoder翻译

翻译成变分自编码器，为什么？？？

“变分”这个词指的是使用变分推断（Variational Inference）的技术。变分推断是一种用于近似复杂概率分布的技术。在变分自编码器中，它用于近似潜在变量的后验分布，因为这些分布往往是难以直接计算的。

VAE中的“variational”翻译为“变分”是为了反映其核心技术——变分推断，这是一种用于处理和近似难以解析求解的概率分布的数学方法。

1. 核心思想

自编码器AE一般用于降维或者特征学习，一般由编码器和解码器两个部分组成。AE的缺点在于，能对输入图进行重建，却不能生成新的图。根本原因是，AE学习的隐变量是确定的、离散的，没有很好的解释性。（给一张图像，得到确定的隐变量，解码出重建的）

变分自编码VAE 核心思想：将隐变量看成一个概率分布，具有不确定的、连续的特点，而且可以生成不同于输入图像的样本。希望能定义一个从隐变量生成样本的模型。

2.技术难点（直接积分方式）

训练生成模型一般通过对数似然函数极大化来求解模型参数，即：，其中训练集包括N个i.i.d的训练样本。

图像生成过程可以表示为：先从隐变量分布采样得到，然后再根据条件分布中采样生成样本，即：

如何将概率转换成网络？？？

• ，隐变量z先验分布，可以设计为简单的高斯分布
• ，条件分布，可以用一个神经网络学习（解码器）

但，积分的过程存在困难，理论上需要对所有的精确遍历，行不通！！!

VAE解决该技术难点的想法：虽然不能求解准确的对数似然函数，但可以设法得到对数似然函数的下界，然后最大化其下界（Evidence Lower Bound），相当于近似地令对数似然函数最大化。

3. 技术实现（考虑后验概率分布解出P(X)）

 遍历不行，那么考虑隐变量的后验分布，能否算出

 (Eq1)，可以推导出，但也难以求解！！！

引入一个新的概率分布 来逼近后验分布.

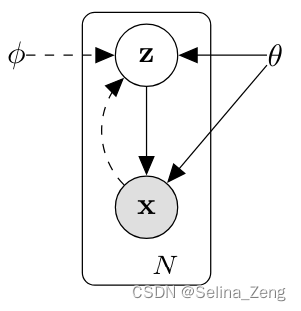
• 实线表示生成模型，解码器
• 虚线表示用变分近似难以解析的后验分布

如此一来，大致模型结构就定了。

下面解决如何优化的问题，近似对数似然函数

                         Eq(1)

                        

                        

                        

                         

                        变分下界Evidence Lower Bound (ELBO)

                        

最大化变分下界，以近似最大化log似然函数。

将变分下界做为损失函数，即可实现VAE核心难点。

公式第二项

• 本质上，对隐变量分布进行了一个“规划化”
• ，计算z的后验分布和隐变量先验分布的KL散度。
  • 假设1：隐变量先验分布为D维高斯分布，由于不包含任何未知参数，重写为
  • 假设2：隐变量后验分布的近似分布为各分量独立的高斯分布，即：每个样本对应一个D维高斯分布

实现：使用两个神经网络编码器（）分别求解均值和方差的对数（因为方差对数值域为实数，更便于计算）。

1. 
2. 

第一个编码器输出均值为D维向量，方差为D维向量

如此以来，就可以计算KL散度。本质上，对隐变量分布进行了一个“规划化”，VAE训练编码器希望KL散度达到最小，令后验近似分布趋近于高斯分布。即，每个样本都像高斯分布靠拢。

公式第一项

• 本质：希望样本重构误差最小
• 我们使用经验近似， 。不需要采样很多z来计算log()，只需要从中采样一次，实际效果证明约等于是成立的
• 下面假设的分布
  • 如果是伯努利分布，解码器，输出为，把编码器最后一层激活函数设置为sigmoid，使用二分类交叉熵作为解码器的损失函数
  • 如果是高斯分布，解码器，输出为，把编码器最后一层设置为值域为全体实值得激活函数，使用MSE为损失函数

4. 复盘（overview理解）

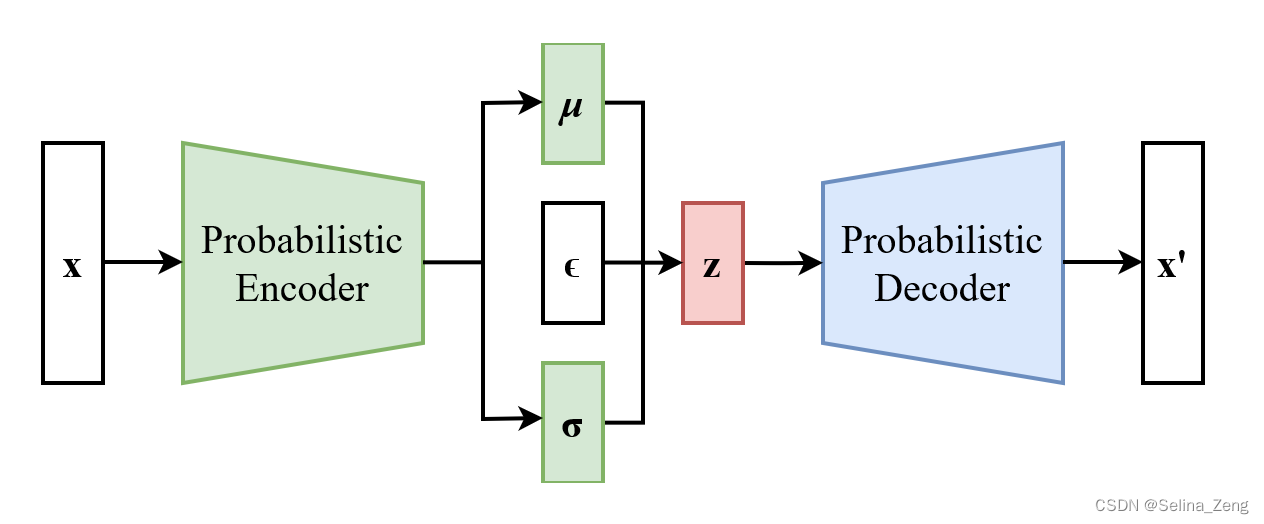
过程：样本x输入编码器得到隐变量后验的近似分布的各项参数D维的均值和log方差。再从(学习的)分布中采样z进入解码器，最后计算损失函数（重构损失+隐变量规范化）。

如何解决从分布中采样不可导的问题？？？

需要把和与解码器建立联系，使其可以反向传播。令：，直接在标准分布中得到。

VAE论文提出了一个重参数技巧，它把从分布中采样的过程改写成从标准高斯分布采样并进行线性变换。这样梯度就可以直接反向传播了。

 5.其他参考资料

1. 首个ICLR时间检验奖出炉！3万被引论文奠定图像生成范式，DALL-E 3/SD背后都靠它

2.《生成对抗网络GAN，原理与实践》言有三

VAE核心代码：

# VAE 模型
class VAE(nn.Module):
    def __init__(self, encoder_layer_size, latent_size, decoder_layer_sizes, conditional=False, num_labels=0):
        super().__init__()
        if conditional:
            assert num_labels>0
        assert type(encoder_layer_sizes)==list
        assert type(latent_size)==int
        assert type(decoder_layer_sizes)==list
        self.latent_size = latent_size
        self.encoder = Encoder(encoder_layer_sizes, latent_size, conditional, num_labels)
        self.decoder = Decoder(decoder_layer_sizes, latent_size, conditional, num_labels)

    def forward(self, x, c=None):
        if x.dim() > 2:
            x = x.view(-1, 28*28)
        means, log_var = self.encoder(x, c)
        z = self.reparameterize(means, log_var)
        recon_x = self.decoder(z, c)
        return recon_x, means, log_var, z

    def reparameterize(self, mu, log_var):
        std = torch.exp(0.5 * log_var)
        eps = torch.randn_like(std)
        return mu + eps*std

    def inference(self, z, c=None):
        recon_x = self.decoder(z, c)
        return recon_x
        

# 编码器

class Encoder(nn.Module):
    def __init__(self, layer_sizes, latent_size, conditional, num_labels):
        super().__init()
        self.conditional = conditional
        if self.conditional:
            layer_sizes[0] += num_labels

        self.MLP = nn.Sequential()

        for i, (in_size, out_size) in enumerate(zip(layer_sizes[:-1], layer_sizes[1:])):
            self.MLP.add_module(name="L{:d}".format(i), module=nn.Linear(in_size, out_size))
            self.MLP.add_module(name="A{:d}".format(i), module=nn.ReLU())

        self.linear_means = nn.Linear(layer_sizes[-1], latent_size)
        self.linear_log_var = nn.Linear(layer_sizes[-1], latent_size)

    def forward(self, x, c=None):
        if self.conditional:
            c = idx2onehot(c, n=10)
            x = torch.cat((x,c), dim=-1)
        x = self.MLP(x)
        means = self.linear_means(x)
        log_vars = self.linear_log_var(x)
        
        return means, log_vars

# 解码器

class Decoder(nn.Module):
    def __init__(self, layer_sizes, latent_size, conditional, num_labels):
        super().__init__()
        self.MLP = nn.Sequential()
        self.conditional = conditional
        if self.conditional:
            input_size = latent_size + num_labels
        else:
            input_size = latent_size

        for i, (in_size, out_size) in enumerate(zip([input_size]+layer_sizes[:-1], layer_sizes)):
            self.MLP.add_module(name="L{:d}".format(i),module=nn.Linear(in_size, out_size))
            if i+1<len(layer_sizes):
                self.MLP.add_module(name="A{:d}".format(i),module=nn.ReLU())
            else:
                self.MLP.add_module(name="Sigmoid", module=nn.Sigmoid())

    def forward(self, z, c):
        if self.conditional:
            c = idx2onehot(c, n=10)
            z = torch.cat((z,c), dim=-1)
        x = self.MLP(z)
        
        return x