热膨胀和热传导

非简谐项

原子间的相互作用：

$$v(a+\delta)=v(a)+\dfrac{\mathrm dv}{\mathrm d r}\delta+\dfrac12\dfrac{\mathrm d^2v}{\mathrm dr^2}\delta^2+o(\delta^2)$$
之前在讨论原子间的相互作用的时候，只用到展开式的前三项，而忽略了更高次的项（非简谐项）。在这样的近似下原子是相互线性独立的谐振子，能够处理振动问题。不过在涉及到热膨胀和热传导等问题时，仅仅用到前三项是不够的。

谐振子之间独立，意味着不发生能量的交换，不能传出能量，也不能吸收能量，所以就不能解决热传导、热平衡、热辐射等问题。

热膨胀

热膨胀 压力不变的情况下，晶体的体积随着温度升高而增大的现象。

原因：分子间相互作用的非简谐项。

原子离开平衡位置的平均偏移量$\bar x$

$$\overline{x}=\dfrac{\int xe^{\frac{U}{k_BT}}\mathrm dx}{\int e^{\frac{U}{k_BT}}\mathrm dx}$$
如果用 $U=\dfrac12\beta x^2$计算，总有 $\overline {x}=0$，即无论温度是多少，分子都不会发生偏移，也就不能解释膨胀现象。

如果用$U=\dfrac12\beta x^2+\dfrac16\gamma x^3$计算，

$$\begin{array}q \overline{x}=\dfrac{\int xe^{\frac{U}{k_BT}}\mathrm dx}{\int e^{\frac{U}{k_BT}}\mathrm dx}\\ =\dfrac{\int xe^{\frac{\frac12\beta x^2}{k_BT}}e^{\frac{\frac16\gamma x^3}{k_BT}}\mathrm dx}{\int e^{\frac{\frac12\beta x^2}{k_BT}}e^{\frac{\frac16\gamma x^3}{k_BT}}\mathrm dx}\\ =\dfrac{\int xe^{\frac{-\frac12\beta x^2}{k_BT}}(1-\dfrac16\gamma x^3)\mathrm dx}{\int e^{\frac{-\frac12\beta x^2}{k_BT}}(1-\dfrac16\gamma x^3)\mathrm dx}\\ =\dfrac{0-\dfrac16\gamma \int x^4e^{\frac{-\frac12\beta x^2}{k_BT}}\mathrm dx}{\int e^{\frac{-\frac12\beta x^2}{k_BT}}\mathrm dx-0}\\ =\dfrac{\dfrac{\gamma k_BT}{\beta^2}\sqrt{\dfrac{2\pi k_BT}{\beta}}}{\sqrt{\dfrac{2\pi k_BT}{\beta}}}\\ =\dfrac{\gamma k_BT}{\beta^2} \end{array}$$
所以 $$r=r_0+\bar x=r_0(1+\alpha T)$$
其中
$$\alpha=\dfrac{\gamma k_B}{r_0\beta^2}$$
称为膨胀系数。

热传导

• 热传导 晶体中热量由高温处流向低温处的现象。
• 热流密度 单位时间内经过单位面积的热量，记为$\mathbf j$。
  热流密度应当正比于温度的梯度
  $$\mathbf j=-K\nabla T$$
  其中$K$称为热传导系数。

温度$T$，频率$\omega$的简正振动的平均能量为

$$\overline{E}=\dfrac12\hbar\omega+\dfrac{\hbar\omega_i}{e^{\hbar\omega_i/k_BT}-1}$$

由于研究温度较高的情形，忽略零点能。引入平均声子数

$$\bar n = \dfrac{1}{e^{\hbar\omega_i/k_BT}-1}\approx \dfrac{k_BT}{\hbar \omega}\propto T$$
有 $$\bar E(\omega)=\bar n \hbar \omega$$

微观解释：温度高的地方振动幅度大、振动模式多，可以认为有更多的声子被激发。当格波传播到低温处（同时也是声子扩散的过程），低温处的格波振动趋于和高温处相同，这样就实现了热量的传递。即，声子通过碰撞传递能量。

热流的大小，取决于声子的运动速度 $\mu$ 和平均自由程 $\lambda$。$\mu$可以取声速。

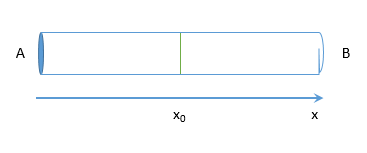
在上面的模型中，设两侧的温度分别为$T_A,T_B$，$T_A>T_B$,平均声子数分别为$\bar n_A,\bar n_B.$由于有六个方向，在$x_0$处由A到B的声子数

$$\dfrac 16\bar n_A\mu\mathrm dt\mathrm dS$$
由B到A的声子数
$$\dfrac 16\bar n_B\mu\mathrm dt\mathrm dS$$
净传导的热量
$$\dfrac 16(\bar n_A-\bar n_B)\mu\mathrm dt\mathrm dS\cdot \hbar \omega$$
$$\begin{array}a j=\dfrac 16(\bar n_A-\bar n_B)\mu\cdot \hbar \omega\\ =\dfrac {\mu}6(\bar E_A-\bar E_B)\\ =\dfrac {\mu}6\dfrac{\partial \bar E}{\partial T}\Delta T\\ =\dfrac {\mu}6\dfrac{\partial \bar E}{\partial T}\dfrac{\mathrm d T}{\mathrm d x}\Delta x\\ =\dfrac {\mu}6\dfrac{\partial \bar E}{\partial T}\dfrac{\mathrm d T}{\mathrm d x}(-2\lambda)\\ =-\dfrac {1}3\mu\lambda C_V\dfrac{\mathrm d T}{\mathrm d x}\\ \end{array}$$
所以
$$K=\dfrac {1}3\mu\lambda C_V$$

---

本文主要参考Dr. Shen 固体物理课件