一文全面解析大模型压缩中的四大关键技术：【知识蒸馏、量化、剪枝、分解】【建议收藏】

引言        

        深度学习模型的压缩和加速是指利用神经网络参数的冗余性和网络结构的冗余性精简模型，在不影响任务完成度的情况下，得到参数量更少、结构更精简的模型。被压缩后的模型计算资源需求和内存需求更小，相比原始模型能够满足更加广泛的应用需求。在深度学习技术日益火爆的背景下，对深度学习模型强烈的应用需求使得人们对内存占用少、计算资源要求低、同时依旧保证相当高的正确率的“小模型”格外关注。本文在从整体上全面解析大模型压缩中的四大关键技术：【知识蒸馏、量化、剪枝、分解】。

目录

一、知识蒸馏（Knowledge Distillation，KD）

1.1、定义

1.2、核心思想

1.3、关键实现技术

1.4、应用场景

1.5、优缺点

1.6、相关论文

二、量化（Quantization）

2.1、定义

2.2、核心思想

2.3、关键技术

2.4、应用场景

2.5、优缺点

2.6、相关论文

三、剪枝（Pruning）

3.1、定义

3.2、核心思想

3.3、关键技术

3.4、应用场景

3.5、优缺点

3.6、相关论文

四、分解（Factorization）

4.1、定义

4.2、核心思想

4.3、关键技术

4.4、应用场景

4.5、优缺点

4.6、相关论文

五、总结

---

序号	内容
1	一文全面解析大模型压缩的四大关键技术：【知识蒸馏、量化、剪枝、低秩分解】【建议收藏】
2	深度解析大模型压缩技术一：知识蒸馏
3	深度解析大模型压缩技术二：量化
4	深度解析大模型压缩技术三：剪枝
5	深度解析大模型压缩技术四：分解

一、知识蒸馏（Knowledge Distillation，KD）

1.1、定义

知识蒸馏（KD）是一种将原始模型（在这种情况下称为教师模型）中的知识提炼或转移到一个较小的模型（可以称之为学生模型）中，从而实现模型压缩的技术。

1.2、核心思想

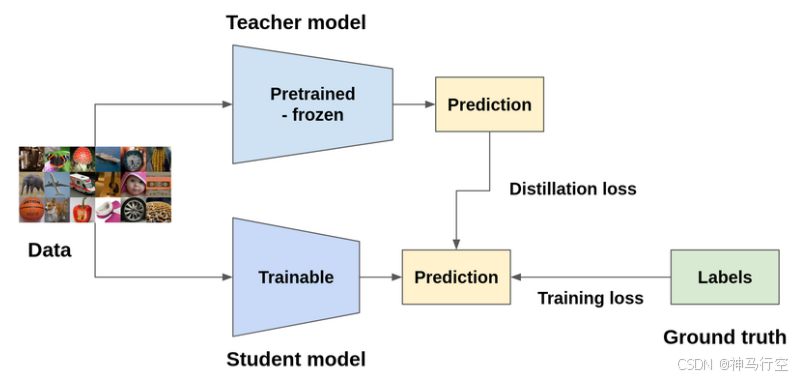
核心思想是让学生模型模仿教师模型的输出分布或中间特征，而非仅学习原始标签。这一过程类似于知识传承，教师模型的“暗知识”（Dark Knowledge）通过软标签（Soft Labels）或中间层特征传递给学生模型。知识蒸馏是一种灵活的模型压缩技术，因为生成的模型可以具有与原始模型不同的架构。

• 软标签（Soft Labels）：教师模型输出的概率分布（经温度参数平滑）比硬标签（Hard Labels）包含更多信息，例如类别间的相似性。

• 特征对齐：学生模型学习教师模型的中间层特征（如注意力矩阵、隐藏层激活值），增强表达能力。

1.3、关键实现技术

实现这一目标的方法有多种，但最常见的方法是尝试使教师模型的输出或中间特征表示与学生模型相匹配。有趣的是，使用真实标签和教师模型输出的软标签组合训练的学生模型，其性能优于仅使用真实标签训练的学生模型，有时甚至能达到教师模型的性能。对于这种行为的一种假设是，由于软标签包含比真实标签（硬标签，例如zero-shot）更多的信息，它有助于学生模型更好地泛化。

1. 软标签与温度参数：教师模型输出经过温度参数（Temperature）平滑后的概率分布，学生模型通过交叉熵损失学习这种分布，避免对极端值的过度拟合。

2. 多层蒸馏：除了输出层，学生模型还可以学习教师模型的中间特征，如嵌入层、注意力矩阵（如TinyBERT）或隐藏层状态（如BERT-PKD）。

3. 多任务学习：结合标签预测和推理过程生成，如Google的“Distilling Step-by-Step”方法，通过提取教师模型的思维链（Chain-of-Thought），提升学生模型的泛化能力。

1.4、应用场景

自然语言处理（如BERT压缩）、移动端部署（轻量模型）、模型隐私保护。

1.5、优缺点

• 优点：显著压缩模型体积，提升推理速度，保留教师模型的泛化能力。

• 缺点：依赖高质量教师模型，训练时间较长。

1.6、相关论文

• [Hinton et al., 2015] Distilling the Knowledge in a Neural Network

  • 提出经典蒸馏框架，引入温度参数和软标签概念。

• [Sanh et al., 2019] DistilBERT, a distilled version of BERT

  • 通过减少BERT层数和结合蒸馏损失，压缩模型至40%大小。

• [Jiao et al., 2020] TinyBERT: Distilling BERT for Natural Language Understanding

  • 全层蒸馏方法，覆盖嵌入层、注意力矩阵和预测层。

二、量化（Quantization）

2.1、定义

量化通过降低模型参数的数值精度（如32位浮点数→8位整数）减少存储和计算开销，同时尽量保持模型性能。

2.2、核心思想

基于量化的模型压缩背后的主要思想是降低模型权重的精度，以减少内存和延迟。通常情况下，深度学习模型在训练期间或训练后将其权重存储为32位浮点数（FP32）。通过量化，这些权重通常被转换为16位（FP16）或8位（INT8）精度，以便在运行时部署。

• 精度-效率权衡：用低精度数值近似高精度参数，牺牲微小精度损失换取显著加速。

• 硬件友好性：整数运算在CPU/GPU上比浮点运算更快且能耗更低。

2.3、关键技术

• 训练后量化（Post Training Quantization，PTQ）：直接训练出一个浮点模型直接对模型的参数进行直接量化。这种方法比较常见于对一个大模型进量化，而对小模型会导致大幅度的性能降低。主要原因有两个：1）post-training对参数取值的要求需要比较大的范围。如果参数的取值范围比较小，在量化过程中非常容易导致很高的相对误差。2）量化后的权重中的一些异常的权重会导致模型参数量的降低。

• 量化感知训练（Quantization Aware Training，QAT）：在训练中模拟量化行为，在训练中用浮点来保存定点参数，最后inference的时候，直接采用定点参数。在训练中模拟量化误差，提升模型鲁棒性。使用较低精度权重和激活进行训练的主要问题是没有正确定义梯度，因此无法进行反向传播。为了使用QAT解决这个问题，该模型模拟了前向传播过程中的目标精度，但使用后向传播的原始精度来计算梯度。

从数学的角度来看，给定权重/激活的量化和校准涉及确定两个值：比例因子和零点。假设想要将FP32转换为INT8：

Python 
1 # max_int for INT8 would be 255 and min_int 0
2 # max_float, min_float are deteremined in the calibration process
3 scale = (max_float - min_float) / (max_int - min_int)
4
5 # to allow for both positive and negative values to be quantized
6 zero_point = round((0 - min_float) / scale)
7
​8 int8_value = round(fp32_value / scale) + zero_point

2.4、应用场景

• 移动端/边缘设备部署、FPGA/ASIC硬件加速。

2.5、优缺点

• 优点：大幅减少内存占用，加速推理，兼容硬件优化。

• 缺点：极端量化（如二值化）可能导致精度显著下降。

2.6、相关论文

• [Han et al., 2015] Deep Compression

  • 结合剪枝、量化和霍夫曼编码，压缩模型至1/35~1/49大小。

• [Jacob et al., 2018] Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference

  • 提出整数量化方案，支持纯整数运算推理。

• [Rastegari et al., 2016] XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks

  • 二值化权重和激活，通过位运算加速卷积计算。

三、剪枝（Pruning）

3.1、定义

剪枝通过移除模型中冗余的参数或结构（如神经元、滤波器、层）来简化网络，分为结构化剪枝（移除整个结构）和非结构化剪枝（移除单个权重）。

3.2、核心思想

• 稀疏性假设：大部分参数对模型贡献微小，移除后对精度影响有限。

• 迭代优化：逐步剪枝并微调，避免一次性剪枝导致性能崩溃。

 通过剪枝，可以从神经网络中移除不太重要的权重（神经元连接）或层，从而使模型变得更小。一个简单的策略是，如果某个神经元连接的权重低于某个阈值，则将其移除。这被称为权重剪枝，它确保移除的是冗余的连接或者是对最终结果影响不大的连接。同样，可以根据神经元重要性的一些指标来移除神经元本身，例如输出权重的L2范数。这被称为神经元剪枝，通常比权重剪枝更有效。

 与节点剪枝相比，权值剪枝会导致稀疏网络，这在GPU等硬件上很难优化。虽然它会减少内存占用和FLOPS，但可能不会降低延迟。剪枝的思想也可以扩展到卷积神经网络（CNN），其中过滤器/内核的相对重要性可以根据其L1/L2范数来确定，并且只能保留重要的过滤器。在实践中，剪枝是一个迭代过程，将在剪枝和微调模型之间交替进行。使用这种方法，可以在性能下降最小的情况下，将网络参数减少50%以上，如下图所示：

3.3、关键技术

• 重要性评估：

  • 权重幅值：移除绝对值小的权重（L1/L2范数）。

  • 梯度敏感度：基于损失函数对参数的敏感度（如SNIP算法）。

  • 特征重建：最小化剪枝后特征图的误差（如ThiNet）。

• 自动化剪枝：使用强化学习或遗传算法搜索最优剪枝策略。

3.4、应用场景

• 高计算资源需求场景（如实时视频处理）、嵌入式设备部署。

3.5、优缺点

• 优点：显著减少参数量和计算量，可能提升泛化能力。

• 缺点：非结构化剪枝需专用硬件支持稀疏计算，否则加速有限。

3.6、相关论文

• [Han et al., 2015] Deep Compression

  • 经典三阶段框架（剪枝→量化→编码），压缩VGG-16至1/49大小。

• [Li et al., 2016] Pruning Filters for Efficient ConvNets

  • 基于滤波器L1范数的结构化剪枝，减少通道数。

• [He et al., 2019] Filter Pruning via Geometric Median

  • 通过几何中位数识别冗余滤波器，提升剪枝鲁棒性。

四、分解（Factorization）

4.1、定义

分解通过矩阵或张量分解（如SVD、CP分解）将大型权重矩阵拆解为多个低秩小矩阵，减少参数数量和计算复杂度。

4.2、核心思想

• 低秩近似：利用矩阵的低秩特性，用更少参数近似原始权重。

• 计算优化：将大矩阵乘法分解为多个小矩阵运算，加速推理。

4.3、关键技术

• 奇异值分解（SVD）：将权重矩阵 W 分解为，保留前k个奇异值。

• 张量分解（Tensor Decomposition）：处理高阶张量（如卷积核），分解为多个低阶张量。

• 卷积核分解：将大卷积核（如5×5）分解为多个小核（如1×5和5×1）。

对于基本的矩阵分解模型而言，目标是最小化重构误差加上正则化的损失函数：

[ L(U,V)=|X-U V^{\mathrm{T}} |_{F}+\lambda(|\mathbf{U}|_F^2 + |\mathbf{V}|^2_F) ]

这里的 Frobenius 范数用于衡量原矩阵与近似矩阵之间的差异；而 λ 控制着正则项强度以防止过拟合现象的发生。为了求解上述最优化问题，常用的方法有梯度下降及其变种形式（如随机梯度下降）、交替最小二乘法 (ALS) 或者基于贝叶斯框架下的概率矩阵分解(PMF)等算法。

PYTHON代码示例

import numpy as np
from scipy.sparse.linalg import svds

def low_rank_matrix_factorization(X, k=10):
    """
    对输入矩阵执行SVD截断操作得到其低秩逼近
    
    参数:
        X -- 输入矩阵
        k -- 截取奇异值数量
        
    返回:
        U -- 左奇异向量组成的矩阵
        S -- 奇异值构成的一维数组
        Vt-- 右奇异向量转置后的矩阵
    """

    # 执行稀疏svd获取前K个特征分量
    U, s, Vt = svds(X, k=k)

    # 将奇异值转换为对角阵
    Sigma = np.diag(s)

    return U @ Sigma, Vt


if __name__ == "__main__":
    # 创建测试用矩阵
    test_data = np.random.rand(50, 70)
    
    u_approximation, v_transpose = low_rank_matrix_factorization(test_data, k=10)

4.4、应用场景

• 推荐系统：通过分析用户行为记录构建评分矩阵，并对其进行降维处理以便更好地理解用户的偏好趋势；

• 图像压缩：采用低秩特性去除冗余信息达到高效编码目的的同时保持视觉质量不变；

• 自然语言处理(NLP)：在文档主题建模方面发挥重要作用，帮助提取文本中的隐含语义关系；

• 生物信息学领域内的基因表达数据分析：识别不同条件下样本间的相似性和差异性，辅助疾病诊断等工作开展。

4.5、优缺点

• 优点：数学理论完备，可显著减少参数。

• 缺点：分解过程可能引入误差，需重训练恢复性能。

4.6、相关论文

• [Jaderberg et al., 2014] Speeding up Convolutional Neural Networks with Low Rank Expansions

  • 通过低秩分解加速卷积计算，在场景文字识别中实现2.5倍加速。

• [Kim et al., 2015] Compression of Deep Convolutional Neural Networks for Fast and Low Power Mobile Applications

  • 应用张量分解（Tucker分解）压缩模型参数。

• [Denton et al., 2014] Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation

  • 使用SVD分解全连接层，减少90%参数。

五、总结

这些模型压缩算法可以单独应用，也可以结合使用来进一步提高模型的压缩效果。它们都是为了在减少模型大小和计算量的同时，尽可能保持模型的预测准确度和泛化能力。实际应用中，往往会结合几种方式使用，以实现最大化压缩效果。常见结合应用：

1. 联合优化：

   • 剪枝+量化（如Deep Compression）：先剪枝稀疏权重，再量化剩余参数。

   • 蒸馏+分解：教师模型分解后作为学生模型的初始化。

   • 蒸馏+量化：通过量化蒸馏损失优化学生模型的低精度权重。

   • 多模态剪枝蒸馏：如蚂蚁集团的AntGMM模型，结合多阶段剪枝和蒸馏损失设计，显著降低延迟和能耗。

2. 硬件适配：量化适配移动芯片，结构化剪枝适配GPU的并行计算。

3. 前沿方向：

   • 动态压缩：根据输入动态调整模型结构（如SkipNet）以减少冗余计算。

   • 自动化压缩：结合NAS自动搜索剪枝/量化策略（如AMC）。

   • 硬件适配：针对特定硬件（如NPU）设计专用压缩方案。

通过灵活组合这些技术，可在模型大小、速度和精度间达到最优平衡。

欢迎 点赞👍 | 收藏⭐ | 评论✍ | 关注🤗