绘制顺滑的贝塞尔曲线

绘制顺滑的贝塞尔曲线

在面试的时候有问到这个问题：有一组点，通过这组点绘制一条曲线，非折线。

当时没答出来，回来后，在网上查了下，目前来说，找个了三个相关的解答：

• Draw Graph curves with UIBezierPath
• 使用贝塞尔曲线绘制多点连接曲线
• Draw smooth curves through a set of points in iOS-需fanqiang

其中 使用贝塞尔曲线绘制多点连接曲线讲解的很仔细，能实现不错的效果

Draw smooth curves through a set of points in iOS讲解的也非常仔细，但我只能看懂部分(￣.￣)，数学没学好啊，其大致的原理是，如下图所示：

如上通过三个点，分成两段来看，就是P0P3-Q0Q3，要满足的条件是：

1.每一段的结束点是另一段的开始点，即P3 = Q0
2.每一段的结束点与其控制点的斜率，与另一段的开始点与其控制点的斜率相同，即P2 — P3/Q0 — Q1共线

其中第2个条件是非常重要的，否则的话绘制的曲线就可能是如下的样子：

下面就是数学原理了：

三次方贝塞尔曲线公式如下：

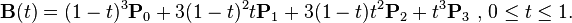
• P0与P3表示曲线的端点，P1, P2表示控制点

上面的公式也可以写作：

Eq. 01

求某一点的斜率，就是对其求导，结果如下：

Eq. 02

对于第i段，其开始点的斜率应等于第i-1段其结束点的斜率，即：

带入t=0和t=1，可得：

Eq. 03

由于片段是连续的，所以：

K_i表示的是第i个点

带入K_i后，得到如下的结果：

Eq. 04

n阶的贝塞尔曲线的导数是是一个n-1阶的贝塞尔曲线，对三阶贝塞尔曲线再求导，得如下的结果：

Eq. 05

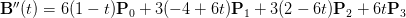
三阶贝塞尔曲线再求导后，其也是连续的，所以，考虑开始点和结束点：

Eq. 06

由于P_0,i等于P_3,i-1（条件1），所以：

Eq. 07

……

后面的就不怎么明白了……，貌似使用的是线性代数来解方程

其demo例子在Ramshandilya/Bezier

源码是swift3的，大家可以修改为swift4，我也照着它，写了个OC版本的，例子的效果如下：

Demo地址