多目标优化系列（一）NSGA-Ⅱ

原文：A Fast and Elitist Multiobjective Genetic Algorithm:
NSGA-II
翻译版：https://wenku.baidu.com/view/61daf00d0508763230121235.html

NSGA-Ⅱ中文名是：一个快速和精英机制的多目标遗传算法。本文是作者接触的第一篇多目标算法论文，所以本文尽量引用原文的知识来聚合成一篇通俗易懂的小作。

摘要：

该文致力于解决的问题：

• O（MN3）的时间复杂度
• 非精英机制的方法
• 需要制定共享参数

引言

通过引出NSGA的缺点，并通过对这些问题的研究提出NSGA-Ⅱ。

1. 支配排序的高时间复杂度：复杂度是O（MN3）。M表示目标函数的数目，N代表种群的数目。
2. 缺少精英机制：
3. 需要制定共享参数：为了保存种群多样性需要依赖共享。

经营机制的多目标进化算法的近况：

MOGA、NPGA、MOEA属于最早的进化算法。

• 基于非支配排序给种群指定适应度
• 在同一支配前沿面保持多样性

SPEA

• 提出了一个带有非支配概念的精英机制多重判据进化算法。建议在每一子代中维持一个外部种群用于保存从开始到至今找到的非支配解。

正文

A. 快速非支配排序方法

O(MN3)方法：确定非支配前沿面，每一个解与其他解比较判断是否支配，故每个解的时间复杂度是O（MN），要找到第一前沿面需要判断每个解，故时间复杂度是O（MN2），要找到所有的前沿面最坏的时间复杂度是O（MN3）。
本文提出的O（MN2）方法：

step1. 确定两个实体：np表示被多少解支配，是一个数目，Sp表示该解所支配的解的集合，如下图所示，D点被A和C点支配，所以D点的np为2，A点支配D和E，所以A点的Sp={D，E}。

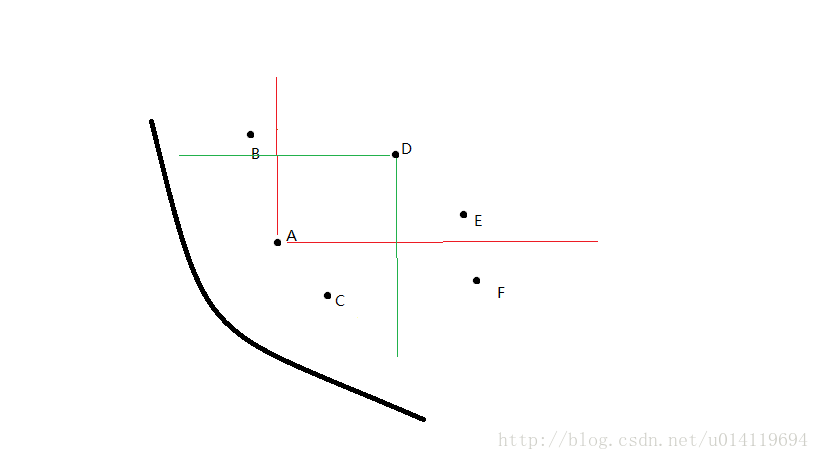
step2. 初始化，两个实体初始化都为0，通过两层循环来获得上述两个实体的值，该步时间复杂度是O（MN2）。
step3 对第一非支配面，即np为0 的解，访问其集合Sp中的每个解然后把其np-1。重复该步，即可得到所有的非支配面。由于每个解最多由N-1个支配，所以每个解被访问的次数最多为N-1次。所以该步时间复杂度为O（N2）。
综上所述，该文提出的计算非支配排序的时间复杂度为O（MN2）。

B. 保留多样性

该文提出了拥挤比较方法替换了共享函数法。

• 密度估计：根据每一目标函数计算该点两侧的两个点的平均距离，该值作为以最近邻居作为顶点的长方体周长的估计（作为拥挤系数）。如下图，第i个解的拥挤系数为他周围长方体的长度（虚线表示）。计算拥挤系数需要对每一目标函数进行排序。
  

• 拥挤算子比较：
  

这里对拥挤系数的算法展示一下：
其中 I[i].m 代表集合I中第i个个体第m个目标函数值。I[i]越大代表该点的密度小，越容易被选中。

以上A和B里面的两点就是该文解决的问题，接下来则是主程序。

C. 主程序

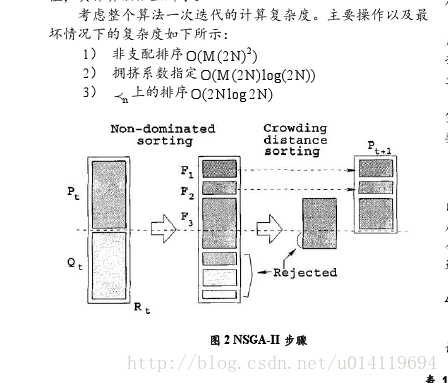
先按照非支配面进行排序，然后对每个支配面里的拥挤算子进行排序，找出前N个点，主要思想如上述B里的第二点。