Indicator-Based Selection in Multiobjective Search
中文名:基于指标的多目标选择
由于这篇文章描述较为简单,所以我们直接展开正题。
正文
思想
对于上图的问题,我们怎么判断A集合和B集合(如果最小为最优)的优劣性。该文运用了下图中的指标
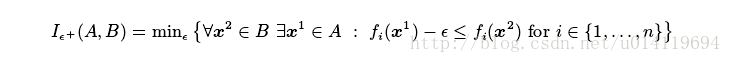
首先该指标代表的前两幅图,而右边的两幅图则又是另一种指标。
我们对该指标描述一下,从上图中第一幅图看,假设A点即X1,B点即X2,对与垂直方向,
我们分析一下该指标,当A->B,即
算法

为了方便起见,我先把原始算法在这里展示一下,然后用中文翻译:
约定:α表示种群大小,N表示最大迭代次数,
step1: 产生初始种群P,种群大小为α,当前迭代此时m=0
step2: 适应度计算,根据一下公式计算P里个体的使用度,例如x1(k为比例缩放因子,参数)
step3: 对每一代P,执行如下运算(缩减),直到种群大小为α
- 选择适应度最小的解
- 从种群中去掉该解
- 更新剩余解的适应度值
step4: 终止条件判断
step5: p’ 为p 的复制,
step6: 用交叉变异作用在p’上,p=p’+p,m=m+1,转step2。
[1]基于加法ε~+指标的多目标优化方法研究(知网)








 本文介绍了一种基于指标的多目标选择方法,通过定义特定的指标来评估解集之间的优劣性。针对不同维度的差距,算法通过迭代选择、适应度计算与种群缩减等步骤,实现对最优解的有效搜索。
本文介绍了一种基于指标的多目标选择方法,通过定义特定的指标来评估解集之间的优劣性。针对不同维度的差距,算法通过迭代选择、适应度计算与种群缩减等步骤,实现对最优解的有效搜索。


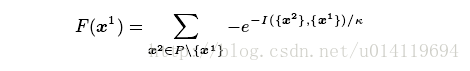

















 2861
2861

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








