按:计算机组成课程第四周作业
算法证明
图表 1 浮点数的表示
浮点数的表示如上图所示,我们要做的是将按如上方式存储的两个浮点数相乘,将其结果用如上的方式表示。
符号位只是两者的异或,指数位基本上是两指数的相加,而尾数位就需要在正常的乘法之余考虑到移位(和随之而来的指数为的溢出)和进位的情况。
下面就来讨论一下尾数的运算:
在尾数前补上1,进行无符号数乘法。小数点仅作为算法分析时的记号,实际上不参加运算。用64位的long long类型的数来存储运算结果。
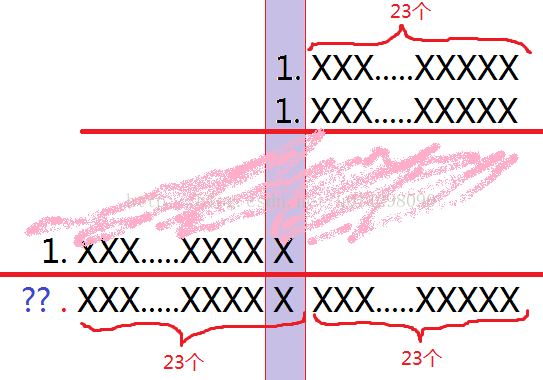
图表 2 尾数相乘(用“画图”程序画的)
如上图所示,后46个数字是结果的小数点后的数据,小数点的的问号处可能只有1,可能是1X(10或11,在算法中没有太大区别)。若问号处只有1,说明已经规格化完成;若是1X,需要将整个数右移一位,质数加一,从而使问号处只有1。
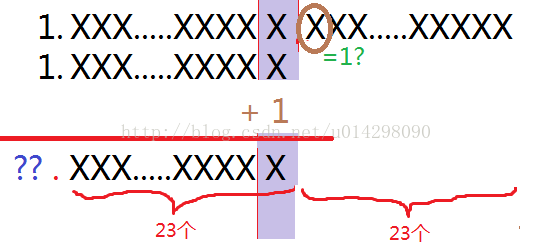
规格化后要进行round操作,如下图所示。如果第23位是0,这一位之前的23位就是所需要的尾数。如果第23位是1,截取这位之前的数,加一(类似于四舍五入)。判断结果是否仍规格化。若没有规格化,从规格化开始继续做,直到找到规格化后的23位尾数。
图表 3 有效数处理(用“画图”程序画的)
程序框图
主要流程如下图所示。在代码注释中的Step1到step5即分别对应流程图中的1至5部分。有所不同的是,因为后面只会增加exponent而








 本文详细介绍了单精度浮点数乘法的算法,包括符号位处理、指数位计算、尾数乘法及规格化过程。通过程序框图和实例分析,展示了算法的运行步骤,并对溢出、特殊输入数据等进行了处理。结果表明,该程序能有效模拟单精度浮点数乘法,与C语言内置浮点数乘法结果一致。
本文详细介绍了单精度浮点数乘法的算法,包括符号位处理、指数位计算、尾数乘法及规格化过程。通过程序框图和实例分析,展示了算法的运行步骤,并对溢出、特殊输入数据等进行了处理。结果表明,该程序能有效模拟单精度浮点数乘法,与C语言内置浮点数乘法结果一致。
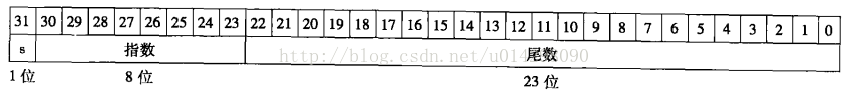
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2363
2363

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








