【基础知识】DDPM中的解码器部分(“L0”)解释以及概率密度函数的解释

1. 前言

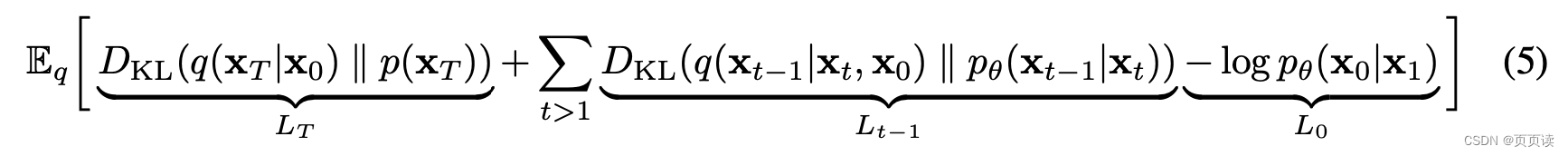
看了很多关于DDPM的博客，都对原文中以上公式的$L_0$没有涉及或者直接说将$L_{t-1}$和$L_0$合并起来讲，这样使得我对这段很困惑。所以，这篇博客我们主要来讲这个解码器$L_0$部分。
在此，之前我们应该理解什么是概率密度函数，我理解是一种衡量"概率的密度的分布"的函数，注意这里不是“概率的分布”，而是“概率密度”的分布，所以想得到概率就需要对此进行积分。
在解码器部分，从公式来看高斯分布$N(x;\mu ,{\sigma }^2)$就是对应的概率密度函数，所以，我们想要得到条件概率，需要对函数在区间上进行积分。

下面我们进行详细的解释。

2. 解码器($L_0$部分)的公式

在这个段落中，作者描述了用于深度学习模型中的数据解码器的数学公式。这是用于将通过神经网络的逆过程编码的数据转换回其原始形式的一部分。让我们详细解释这个公式：

首先，作者提到图像数据是从 {0, 1, …, 255} 范围的整数线性缩放到 [-1, 1] 范围内的数。这确保了神经网络的逆过程是在一致缩放的输入上操作的。

为了在逆过程中获得离散的对数似然值（即评估概率模型的好坏），作者设定了逆过程的最后一步是一个独立的离散解码器，它是基于高斯分布$N(x_0;{\mu }_{\theta }(x_1,1),{\sigma }_1^2)$导出的。

公式$p_{\theta }(x_0|x_1)$表示在给定$x_1$的条件下，$x_0$的条件概率。这个概率是对数据维度$D$的每一个独立坐标$i$进行的乘积，即公式中的${\prod }_{i=1}^D$。

对于每个坐标$i$，条件概率$p_{\theta }(x_0|x_1)$是通过在函数 δ + ( x 0 i ) \delta_+(x_0^i)