1. L1 loss:
公式和求导公式:
(带绝对值求导时,先去掉绝对值符号,再分情况求导)

一个batch的形式:

L1 loss 图形和求导图形如下:

图的底部是预测值和label的差值。 我们可以看到L1 loss的底部是尖的。底部是不存在导数的。而在其他地方,导数大小都是一样的。
优缺点:
优点:
1. L1 loss的鲁棒性(抗干扰性)比L2 loss强。概括起来就是L1对异常点不太敏感,而L2则会对异常点存在放大效果。因为L2将误差平方化,当误差大于1时,误会会放大很多,所以使用L2 loss的模型的误差会比使用L1 loss的模型对异常点更敏感。如果这个样本是一个异常值,模型就需要调整以适应单个的异常值,这会牺牲许多其它正常的样本,因为这些正常样本的误差比这单个的异常值的误差小。如果异常值对研究很重要,最小均方误差则是更好的选择。
缺点:
1. L1 loss 对 x(损失值)的导数为常数,在训练后期,x较小时,若学习率不变,损失函数会在稳定值附近波动,很难收敛到更高的精度。
2. L2 loss的稳定性比L1 loss好。概括起来就是对于新数据的调整,L1的变动很大,而L2的则整体变动不大。
2. L2 loss:
公式和求导公式:
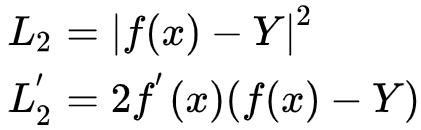
一个batch的形式:

L2 loss图形和求导图像如下:

缺点:
从L2 loss的图像可以看到,图像(上图左边红线)的每一点的导数都不一样的,离最低点越远,梯度越大,使用梯度下降法求解的时候梯度很大,可能导致梯度爆炸。
L1 loss一般用于简单的模型,但由于神经网络一般是解决复杂的问题,所以很少用L1 loss,例如对于CNN网络,一般使用的是L2-loss,因为L2-loss的收敛速度比L1-loss要快。如下图:

3. Smooth L1 loss
计算公式与求导公式:

一个batch(n个)数据时:

smooth L1 loss的图如下:

仔细观察可以看到,当预测值和ground truth差别较小的时候(绝对值差小于1),其实使用的是L2 Loss,当绝对值差小于1时,由于L2会对误差进行平方,因此会得到更小的损失,有利于模型收敛。而当差别大的时候,是L1 Loss的平移,因此相比于L2损失函数,其对离群点(指的是距离中心较远的点)、异常值(outlier)不敏感,可控制梯度的量级使训练时不容易跑飞。。SooothL1Loss其实是L2Loss和L1Loss的结合,它同时拥有L2 Loss和L1 Loss的部分优点。


























 2283
2283

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








