
马尔科夫过程
在概率论及统计学中,马尔可夫过程(英语:Markov process)是一个具备了马尔可夫性质的随机过程,因为俄国数学家安德雷·马尔可夫得名。马尔可夫过程是不具备记忆特质的。换言之,马尔可夫过程的条件概率仅仅与系统的当前状态相关,而与它的过去历史或未来状态,都是独立、不相关的。
一个马尔科夫过程是状态间的转移仅依赖于前n个状态的过程。这个过程被称之为n阶马尔科夫模型,其中n是影响下一个状态选择的(前)n个状态。最简单的马尔科夫过程是一阶模型,它的状态选择仅与前一个状态有关。这里要注意它与确定性系统并不相同,因为下一个状态的选择由相应的概率决定,并不是确定性的。
刻处于状态j的概率aij为一定值。即对任意n≥1,Xn+1对于过去状态的条件概率分布仅是Xn的一个函数
这样的随机过程称为Markov链。
状态转移矩阵
对于有N个状态的一阶马尔科夫模型,共有N*N个状态转移,因为任何一个状态都有可能是所有状态的下一个转移状态。每一个状态转移都有一个概率值,称为状态转移概率——这是从一个状态转移到另一个状态的概率。所有的N*N个概率可以用一个状态转移矩阵表示。
定义下面的矩阵A为状态转移概率矩阵:
满足条件:
1=<i,j<=N.
注意这些概率并不随时间变化而不同——这是一个非常重要(但常常不符合实际)的假设。
隐马尔科夫模型HMM
在正常的马尔可夫模型中,状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中,状态并不是直接可见的,但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。
HMM是一种用参数表示的用于描述随机过程统计特性的概率模型,它是一个双重随机过程。HMM 由两部分组成:马尔可夫链和一般随机过程。其中马尔可夫链用来描述状态的转移,用转移概率描述。一般随机过程用来描述状态与观察序列间的关系,用观察值概率描述。对于HMM模型,状态转换过程是不可观察的,因而称之为“隐”马尔可夫模型。
一个HMM的例子
一个HMM可以由下列参数描述:
1. N:模型中,Markov链的状态数目。记N个状态为θ1,θ2,⋯,θN,记t时刻Markov链所处的状态为qt,显然qt∈(θ1,θ2,⋯,θN)。在罐子和球的实验中罐子就相当于HMM中的状态。
2.M:每个状态对应的可能的观测值数目。记M个观测值为v1,v2,⋯,vM,记t时刻的观测值为Ot,其中Ot∈(v1,v2,⋯,vM)。在罐子和球的实验中所选球的颜色就是HMM模型中的观测值。
3. π:初始概率分布矢量 π =( π1, π2,⋯, πN),其中
πi=P(qt=θi),1=<i<=N.
在罐子和球的实验中,指实验开始时选择的某个罐子的概率。
4.A:状态转移概率矩阵,A=(aij)N*N。其中,
aij=P(qt+1=θj/qt=θi) 1≤i,j≤N
在罐子和球的实验中是指每次选取当前罐子的条件下,选取下一个罐子的概率。
5.B:观测值概率矩阵,B=(bjk)N*M,其中
bjk=P(Ot=vk/qt=θj),1≤j≤N,1≤k≤M
在罐子和球的实验中,bjk就是第j个罐子中球的颜色k出现的概率。
这样,记HMM为:
λ =(N,M,π,A,B)
或简写为:
λ =(π,A,B)
HMM可以分为两部分,一个是Markov链,由π、A来描述,产生的输出为状态序列:另一个随机过程,由B来述,产生的输出为观测值序列。
HMM模型中存在两个假设:一是输出观察值之间严格独立,二是状态的转移过程中当前状态只与前一状态有关(一阶马尔可夫模型)。
HMM基本算法
给定的一个HMM,必需要解决三个基本问题,围绕着三个基本问题,人们研究出了三个基本算法,这三个问题是:
问题1 HMM的概率计算问题
给定观测序列o={ol,o2,⋯,ot}和模型λ,怎样有效地计算观测变量序列o的在给定模型下的概率P(OIλ)
问题2 HMM的最优状态序列问题
给定观测序列O={o1,o2,⋯,ot)和模型λ,怎样选择一个相应的状态序列q={q1,q2,⋯,qt),能够在某种意义上最优(例如,更好的解释“观测变量”)?
问题3:HMM的训练问题(参数估计问题)
给定观测序列O={o1,o2,⋯,ot,)和初始条件,如何调整模型参数λ=(π,A,B)使P(Olλ)为最大?
前向一后向算法
这个算法是上述第一个问题的解决方案。
前向算法
定义前向变量为:αt(i)=P(o1,o2,…,ot,qt=θiIλ),l≤t≤T
那么,有,
a)初始化
α1(i)=πi*bi(o1)
b)递归
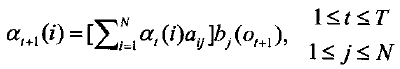
c)终结
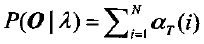
推导过程
后向算法
定义后向变量为:
βt(i)=P(ot+I,ot+2,…,oT|qt=θi,λ),1≤t≤T-1
其中,βT(i)=1,后向算法的计算过程如下:
a)初始化
βT(i)=1,1≤i≤N
b)递归
c)终结
后向算法初始化时对于所有的状态i定义βT(i)=1。
Viterbi算法
问题2是寻求“最优”状态序列。‘‘最优’’的意义有很多种,由不同的定义可得到不同的结论。这里讨论的最优意义上的状态序列Q*,是指使P(Q|O,λ)最大时所确定的状态序列。这实际上是一个动态规划问题。这个过程可以用Viterbi算法来实现。Viterbi算法可以叙述如下:定义δt(i)为t时刻沿一条路径ql,q2,⋯,qt,且qt=θi,产生出o1,o2,⋯,ot的最大概率,即有
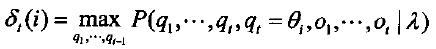
那么求取最优状态序列Q*的过程为:
a)初始化
b)递归
C)终结
其中符号argmax符号定义为,如果i=I,f(i)达到最大值,那么
d)求最佳状态序列
Baum—Welch算法
这个算法解决了上面提到的问题三,即HMM训练或参数估计问题,即给定一个观测值序列O={o1,o2,⋯,oT},该算法能够确定一个模型λ=(π,A,B)使P(Olλ)为最大。这是一个泛函极值问题,因而不存在一个最佳方案来估计λ。在这种情况下,Baum—Welch算法利用递归的思想,使P(Olλ)为局部最大,最后得到模型的参数。其实就是用了EM算法的思想。定义ξt(i,j)为给定训练序列O和模型λ时,时刻t时Markov链处于θi状态和时刻t+1时处于θj状态时的概率,即
ξt(i,j)=P(O,qt=θi,qt+1=θj|λ)
根据前向变量和后向变量的定义可以导出:
ξt(i,j)=[αt(i)aijbj(ot+1)βt+1(j)]/P(Olλ)
那么t时刻Markov链处于θi状态的概率为:
于是.表示从θi状态转移出去的期望值数目,而
表示从θi状态转移到θj状态的期望值数目。由此导出了Baum-Welch算法中著名的重估公式
那么HMM的参数λ=(π,A,B)的求取过程为;根据观测序列O和选取的初始模型λ0=(π,A,B),由重估公式求得一组新的参数露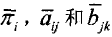
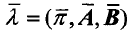
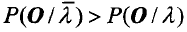
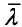
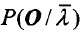
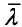
HMM用于模式识别
HMM是一种动态模式识别工具,能够对一个时间跨度上的信息进行统计建模和分类。
在语音识别中,要首先建立一种对应关系,例如,使一个字对应一个HMM,这里的状态就是指这个音所包含的全部可能的音素(或其细分,或其组合)。对应于此字的一个观测样本,这些音素按照一定的先后顺序出现,这就形成了HMM中的状态序列,现实中不可观测到。相应的观测过程的现实就是每个字母所对应的声音信号的振幅。为了建立上述对应关系,首先应对
该字的一组观测样本(该字的若干个声音信号)进行学习,也就是说相应的状态序列缺失的情况下进行HMM的参数估计。用数理统计的语言来说,就是不完全数据的参数估计。
在学习了每个字的参数后,就可以用来识别。也就是对一组观测样本(一个字的声音信号),找到最大可能产生该观测样本的那个模型作为该字的代表。
基于方法的孤立词识别系统的基本思想:在训练阶段,用HMM的训练算法(如Baum一welch算法),建立系统词汇表中每个单词对应的HMM,记为λ。在识别阶段,使用前向一后向算法或Viterbi算法求出各个概率P(O/λi),其中O为待识别词的观测值序列。最后选取最大的P(O/λi))所对应的单词斌为O的识别结果。
<span style="font-size:14px;"><span style="font-size:10px;">import numpy as np
#########author Marsharll#########
#############2015.11.9############
##########version 1.0#############
class DHMM:
#HMM状态为N个,可以观察到的观测数为M
#transition_matrix是N*N的状态转移矩阵
#transition_matrix每一行的概率和为1,不一定对称
#observation_matrix是观测概率矩阵,含义是某时刻t处于状态s的条件下生成观测v的概率,大小为N*M
#observation_matrix每一行和为1
#PI是初始状态概率分布,为N*1元组,含义是初始时刻处于某一状态的概率
def __init__(self,state_num,visible_num):
self.__state_num=state_transition_matrix.shape[0]
self.__visible_num=observation_prob_matrix.shape[1]
self.__transition_matrix=np.zeros(state_num,state_num)
self.__PI=np.zeros(state_num)
self.__observation_matrix=np.zeros(state_num,visible_num)
self.__epsilon=0.0001
#observations为t=1到t=T时刻的观测序列,T*1元组
def __forward(self,observations):
#实质是动态规划算法
#__alpha为N*1矩阵
T=len(observations)
temp=self.__observation_matrix
temp=temp.T
temp1=temp[observations[0]]
self.__alpha=np.zeros(T,self.__state_num)
#1. 初始化:根据observations[0]计算t=0时刻所有状态的局部概率alpha
self.__alpha[0]=np.multiply(self.__PI,temp1)#矩阵对应元素相乘
#2. 归纳:递归计算每个时间点,t=1,… ,T-1时的局部概率
for t in xrange(T-1):#0,1,...T-2
for i in xrange(self.__state_num):
sumnum=0
for j in xrange(self.__state_num):
#弄清楚计算表达式的实际含义,i、j不要弄混淆,时间下标t不要弄错
sumnum+=self.__alpha[t][j]*self.__transition_matrix[j][i]
self.__alpha[t+1][i]=sumnum*self.__observation_matrix[i][observations[t+1]]
#3. 终止:观察序列的概率等于T时刻所有局部概率之和
return np.sum(self.__alpha[T-1])
#后向算法
def __backward(self,observations):
T=len(observations)
#1. 初始化
self.__beta=np.zeros(T,self.__state_num)
for i in xrange(self.__state_num):
self.__beta[T-1][i]=1.0
#2. 递归
for t in xrange(T-2,-1,-1):#T-2,T-3,...,1,0
for i in xrange(self.__state_num):
sumnum=0
for j in xrange(self.__state_num):
sumnum+=self.__transition_matrix[i][j]*self.__observation_matrix[j][observations[t+1]]*self.__beta[t+1][j]
self.__beta[t][i]=sumnum
#3. 终止
return np.sum(self.__beta[0])
def viterbi(self,observations):
#维特比算法,根据观测序列求取隐藏状态的最佳路径
#实质是动态规划算法
#delta[t][i]是t时刻到达状态i的所有序列概率中最大的概率
delta=np.zeros(len(observations),self.__state_num)
#psi记录路径
psi=np.zeros(len(observations),self.__state_num)
#初始化0时刻
for x in xrange(self.__state_num):
delta[0][x]=self.__PI[x]*self.__observation_matrix[x][observations[0]]
psi[x][i]=0
for t in xrange(1,len(observations)):#1,2,...,T-1
for j in xrange(self.__state_num):
for i in xrange(self.__state_num):
#弄清楚计算式的物理含义,i、j不要弄混淆,时间下标t不要用错
if (delta[t][j] < delta[t-1][i]*self.__transition_matrix[i][j]):
delta[t][j] = delta[t-1][i]*self.__transition_matrix[i][j]
#记录到达最大概率时的路径
psi[t][j] = i
delta[t][j] *= self.__observation_matrix[j][observations[t]]
# termination: find the maximum probability for the entire sequence (=highest prob path)
p_max = 0 # max value in time T (max)
path = np.zeros((len(observations)))
for i in xrange(self.__state_num):
if (p_max < delta[len(observations)-1][i]):
p_max = delta[len(observations)-1][i]
path[len(observations)-1] = i
# path backtracing
# path = numpy.zeros((len(observations)),dtype=self.precision)
for i in xrange(1, len(observations)):
path[len(observations)-i-1] = psi[len(observations)-i][ path[len(observations)-i] ]
return path
def __calXi(self,observations):
#计算估计参数时用到的中间变量
xi=np.zeros((len(observations),self.__state_num,self.__state_num))
for t in xrange(len(observations)-1):#0,1,...,T-2
sumnum=0.0
for i in xrange(self.__state_num):
for j in xrange(self.__state_num):
temp=self.__alpha[t][i]*self.__transition_matrix[i][j]*self.__observation_matrix[j][observations[t+1]]*self.__beta[t+1][j]
sumnum+=temp
for i in xrange(self.__state_num):
for j in xrange(self.__state_num):
numerator=self.__alpha[t][j]*self.__transition_matrix[i][j]*self.__observation_matrix[j][observations[t+1]]*self.__beta[t+1][j]
xi[t][i][j]=numerator/sumnum
return xi
def __calgamma(self,xi,T):
#计算估计参数时用到的中间变量
self._gamma=np.zeros(T,self.__state_num)
for t in xrange(T):
for i in xrange(self.__state_num):
self._gamma[t][i]=sum(xi[t][i])
return self._gamma
def __update_trans_matrix(self,observations,xi):
#更新状态转移矩阵
new_trans_matrix=np.zeros(self.__state_num,self.__state_num)
for i in xrange(self.__state_num):
for j in xrange(self.__state_num):
numerator=0.0
denominator=0.0
for t in xrange(len(observations)-1):
numerator+=self.__eta1(t,len(observations)-1)*xi[t][i][j]
denominator+=self.__eta1(t,len(observations)-1)*gamma[t][i]
new_trans_matrix[i][j]=numerator/denominator
return new_trans_matrix
def __eta1(self,t,T):
#控制时间序列中不同观测值的权重,这里都是1
return 1.
def __update_B(self,observations):
#更新状态-观测矩阵
B_new=np.zeros(self.__state_num,self.__visible_num)
for j in xrange(self.__state_num):
for k in xrange(self.__visible_num):
numer = 0.0
denom = 0.0
for t in xrange(len(observations)):
if observations[t] == k:
numer += self._gamma[t][j]
denom += self._gamma[t][j]
B_new[j][k] = numer/denom
return B_new
def __BaumWelch(self,observations):
#非监督学习,估计参数,是训练过程
# E-step
self.__forward(observations)
self.__backward(observations)
xi=self.__calXi(observations)
self.__calgamma(xi,len(observations))
# M-step
newmodel={}
#newmodel["PI"]=self._gamma[0]/double(np.sum(self._gamma[0]))
newmodel["PI"]=self._gamma[0]
newmodel["transition_matrix"]=self.__update_trans_matrix(observations,xi)
newmodel["B"]=self.__update_B(observations)
return newmodel
def __update_model(self,newmodel):
#更新模型参数
self.__PI=newmodel["PI"]
self.__transition_matrix=newmodel["transition_matrix"]
self.__observation_matrix=newmodel["B"]
def train(self,observations,max_iteration=100):
#训练HMM模型参数
prob_old=100000
iteration=0
while(iteration<max_iteration):
iteration+=1
newmodel=self.__BaumWelch(observations)
prob_new=np.log(sum(self.__alpha[-1]))
self.__update_model(newmodel)
#如果概率收敛,结束训练
if(abs(prob_new-prob_old) < self.__epsilon):
break
#否则继续训练
prob_old=prob_new</span></span>HMM的介绍及实现 - 阿凡卢 - 博客园
浅析隐马尔可夫模型











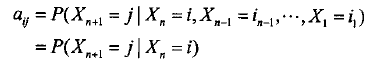
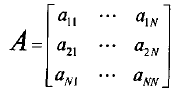
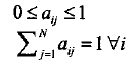
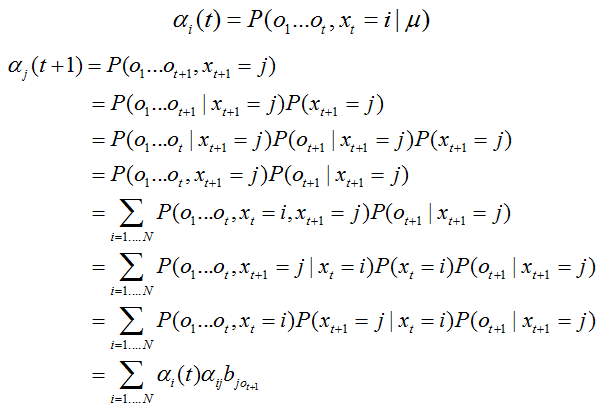

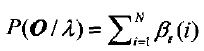
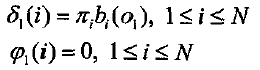
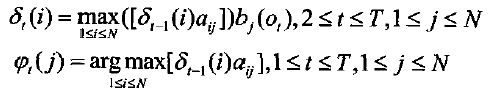
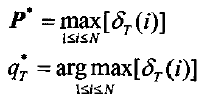
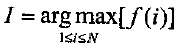
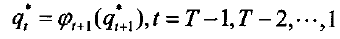
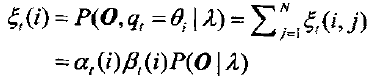
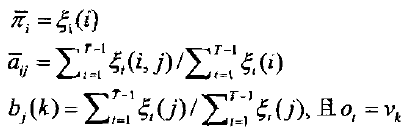














 6895
6895

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








