隐马尔科夫模型（2）

隐马尔科夫模型

1、马尔科夫过程

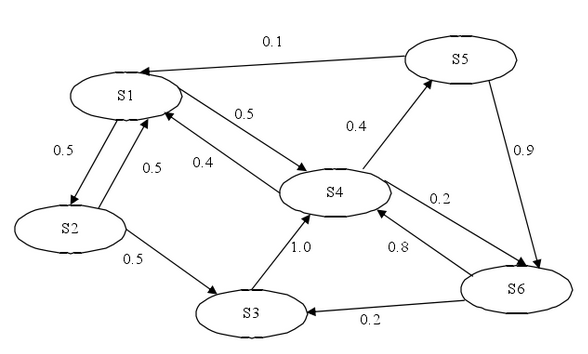
首先回顾一下马尔科夫过程：，其特点是，当过程在时刻 T0所处的状态为已知的条件下，过程在 T 时刻（T>T0）所处的状态仅与时刻T0 有关，而与过程在T0之前的时刻无关系。
马尔科夫模型有两个假设：
-系统在时刻t的状态只与时刻t-1处的状态相关；（也称为无后效性）
-状态转移概率与时间无关；（也称为齐次性或时齐性）

下图是马尔科夫过程得一个图

2、隐马尔科夫模型

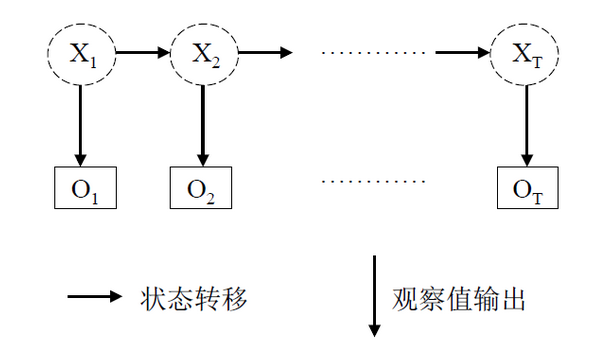
HMM(Hidden Markov Model,隐马尔科夫模型)是一种用参数表示的用于描述随机过程统计特性的概率模型，是一个双重随机过程, 由两个部分组成:马尔可夫链和一般随机过程。 其中马尔可夫链用来描述状态的转移，用转移概率描述。一般随机过程用来描述状态与观察序列间的关系，用观察值概率描述。
对于HMM模型，其的状态转换过程是不可观察的，因而称之为“隐”马尔可夫模型。

该图分为上下两行，上面那行就是一个马尔科夫转移过程，下面这一行则是输出，即我们可以观察到的值。现在，我们将上面那行的马尔科夫转移过程中的状态称为隐藏状态，下面的观察到的值称为观察状态。
观察状态的集合表示为 $O=\{O_1,O_2,O_3,…O_M\}$。相应的，隐马尔科夫也比马尔科夫多了一个假设，即输出仅与当前状态有关，可以用如下公式表示：

$P(O_1,O_2,…,O_t|S_1,S_2,…,S_t)=P(O_1|S_1)*P(O_2|S_2)*...*P(O_t|S_t)$

其中，$O_1,O_2,…,O_t$为从时刻1到时刻t的观测状态序列，$S_1,S_2,…,S_t$则为隐藏状态序列。

另外，该假设又称为输出独立性假设。

HMM定义
1. X代表一组状态的集合,其中$X = { S_1, S_2,..., S_N }$，状态数为 N, 并用 $q_t$来表示t 时刻的状态。虽然状态是隐藏的，但对于很多应用来说，有一些物理的意义都和状态或者状态集相关。状态内部的联系就是从一个状态可以到其它状态。
2. O代表一组可观察符号的集合$O = {V_1,V_2,...,V_M }$，M是从每一状态可能输出的不同的观察值的数目。
3. 状态转移概率分布$A = {a_{ij} }$，这里$a_{ij}= P${$q_{t+1}=S_j| q_{t}=S_i$}。$1<=i,j<=N$特殊情况下，每个状态都可以一步到达其它任何状态，这时对任意$(i, j)有a_{ij} >0$。对于其他的HMM，可能有$a_{ij} ＝0$（对于一对或多对i，j）。
4. 状态 j的观察概率分布$B =$ {$b_ j ( k)$}，表示状态 j输出相应观察值的概率，其中$b_ j ( k)= P${$O_t =V_k | q_t = S_ j$},$1 <=j <= N, 1 <= k<= M$。
5. 初始化状态分布$p = {\pi_i }，\pi = P\{q_1 = S_i \},1 <= i <= N$。

由上，HMM可以定义为一个五元组$l ：l = (X,O,\pi , A, B)$或简写为$l = (\pi , A, B)$
上面所述HMM的三个关键元素实际可以分成两部分，其一为Markov链，由p 、A描述，另一部分是一个随机过程，由B描述.

3、HMM的三个基本问题

3.1 评估问题

给定模型（五元组），给定模型（五元组），求某个观察序列 O的概率
给定观察序列$O= O_1O_2...O_T和模型\lambda = ( A, B,\pi )，计算P(O|\lambda)$。即给定模型和输出观察序列，如何计算从模型生成观察序列的概率。可以把它看作是评估一个模型和给定观察输出序列的匹配程度，由此可以用来在一系列候选对象中选取最佳的匹配

3.2 解码问题

给定模型和观察 序列 O，求可能性最大的隐藏状态序列
给定观察序列$O= O_1O_2...O_T$和模型$\lambda = ( A, B,\pi )$，求在某种有意义的情况下最优的相关状态序列$Q= q_1q_2...q_T$。该可以理解为对输出观察的最佳“解释”，它试图揭示模型的隐藏部分，比如说查找“正确”的状态序列，在应用中，通常都使用一个优化策略来最大可能的解决这个问题。

3.3 学习问题

对于给定的观察 序列 O，调整 HMMHMM 的参数，使观察序列出现的概率最大。
如何调整模型参数$\lambda= ( A, B,\pi )$，对于一个给定的观察序列$O= O_1O_2...O_T$，使得$P(O|\lambda)$最大。它试图优化模型的参数来最佳的描述一个给定的观察序列是如何得来的。

4、解决办法以及相关算法

待续

参考链接1-比较详细
参考链接2-比较详细