布丰投针计算圆周率：Python实现

问题背景

在18世纪的法国，有一位博物学家、数学家，叫布丰。

布丰投针问题：设我们有一个以平行且等距木纹铺成的地板，随意抛一支长度比木纹之间距离小的针，可统计出针和其中一条木纹相交的概率，根据这个概率可以得出圆周率。

布丰以此概率提出了计算圆周率的新方法：随机投针法。

不知道你现在的心情是不是这样：

 随便往地板上扔针，竟然能算出圆周率？？？这两件事，有一点点的关系么？……

为了方便分析，取平面内一个结构单位，该结构单位由某条平行线的某部分和一根针组成。

 

如图，由于y可以取0到d/2的任何数，因此针中点的所有可能性（所有y）构成长为d/2的线段。随着θ的变化，该可能性并不会变化，因此所有可能性形成面积为的粉色矩形。易得：

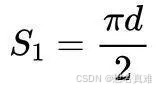
当针中点的位置满足其与平行线相交时，其可能的值为小于等于l/2sinθ 的所有值。随着θ的变化，该可能性变化，因此所有可能性形成面积为S2的蓝色图形。

计算机模拟实验

经过一大串证明后，咱们就来自己投针试试。

1. 使用随机数生成一个点
2. 以这个点为圆心，针的长度为半径画一个圆
3. 随机生成一个[0, 2π] 之间的角度，计算得到终点
4. 有了起点和终点，由此得到了一条完整的针
5. 计算这个针与平行线是否相交
6. 循环10W次，得到相交的次数
7. 代入公式得出计算结果，

完整代码如下： 

import random  
import math

# 生成随机点的范围
RandomWidht = 10000_0000

# 线的长度
LineLength = 80

# 横线与横线之间的间距
LineSpace = 100


class Point(object):
    def __init__(self, x, y):
        super(Point, self).__init__()
        self.x = x
        self.y = y

    def __repr__(self):  
        return f"Point({self.x},{self.y})"  


class Line(object):
    """docstring for Line"""
    def __init__(self, startPoint, endPoint):
        super(Line, self).__init__()
        self.startPoint = startPoint
        self.endPoint = endPoint

    def __repr__(self):  
        return f"Line(起点: {self.startPoint} 终点: {self.endPoint})" 

# 生成随机的线
def createRandomLine():
    startX = random.random() * RandomWidht
    startY = random.random() * RandomWidht
    startPoint = Point(startX, startY)
    
    # 生成一个0到2π之间的随机角度  
    angle = random.random() * 2 * math.pi

    # 使用极坐标转换公式计算圆上点的x和y坐标  
    endX = startX + LineLength * math.cos(angle)  
    endY = startY + LineLength * math.sin(angle)  
    endPoint = Point(endX, endY)
    line = Line(startPoint, endPoint)
    return line


# 判断线是否越过边间
def lineIsCrossBoard(line):

    startY = min(line.startPoint.y, line.endPoint.y)
    endY = max(line.startPoint.y, line.endPoint.y)

    startYOffset = startY / LineSpace
    endYOffset = endY / LineSpace

    result = False
    if int(startYOffset) == int(endYOffset):
        result = False
    else:
        result = True

    return result


def computePi(loopCount):
    crossCount = 0
    for x in range(loopCount):
        line = createRandomLine()
        result = lineIsCrossBoard(line)
        if result:
            crossCount += 1

    # 计算公式:https://baijiahao.baidu.com/s?id=1684796810866685202&wfr=spider&for=pc
    # 2nl/md
    pi = (2*loopCount*LineLength) / (crossCount*LineSpace)
    print(f"循环次数{loopCount}, 相交次数:{crossCount},计算获取到的pi = {pi}")


for x in range(10):
    computePi(10_0000)

    

总结

该方法之所以可以估算π值，是因为进行了转化、变换得到的等式中带有π。

例如，方法二中π的来自于 S1，更本质地说，是来自于针与平行线夹角的积分上限（范围）。实际上这个 π 是从角度中得到。