【数学】通俗解释布丰投针实验过程、蒙特卡洛方法及python仿真代码

很郁闷为什么网上的布丰投针都写的这么复杂，而且很多都是复读机直接copy别人，其实这是个很精巧、有趣的实验，所以打算自己写一个布丰投针的介绍

故事背景

你在教室里写数学题，突然有个人，抱着一大盒针走过来，然后把针撒到地上，然后很淡定地点点头说，“嗯，我知道π等于多少了”。

是不是觉得很神奇？！这跟π什么关系？！！！

没错，这个人就是布丰。

实验过程

这个实验也很简单，两段距离为D的平行线、一根长为L的针（L≤D）

投针实验就是把这根针扔到两段平行线之间，然后统计针碰到平行线的次数，例如图中的两根针，红色针就是碰到，黑色针就是没碰到

哪这和π是怎么扯上关系的呢？是从”针碰到平行线“的数学定义中推导得到的。我们先想办法定义针的位置，取针的中点向最近的平行线做垂线，定义该垂线为$X$，该垂线与针的夹角为$\theta$
因为针是在两段平行线之间，故
$$X\in [0,D/2]$$
同时因为总能找到一个小于90°的角，故
$$\theta \in [0,\pi /2]$$

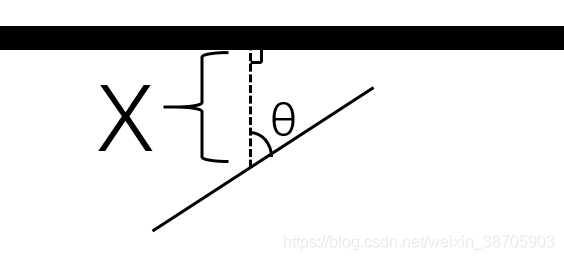
$X$与$\theta$与平行线可以组成一个直角三角形，所以斜边的长度是$X/cos\theta$

因此，只要
$$X/cos\theta <L/2$$
$$即X<(L/2)\ast cos\theta$$
的话（其实取≤也可以，影响不大），就说明针碰到了平行线，否则就说明没碰到，下图分别为”没碰到和“碰到”的情况

下面我们来表示出“针碰到平行线的概率”，即
P { X < L 2 c o s θ } P\{X<\frac{L}{2}cosθ\} P{ X<2L​cosθ}

求概率，本质就是比值，而因为$X$与