支持向量机(SupportVectorMachine)笔记

Prequisite

• 吃饱喝足

分类

简要说一下SVM的分类：

• 线性可分SVM
• 线性不可分SVM
  1.软间隔法
  2.核技巧

线性可分SVM

引入

假设给定训练集：
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x n , y n ) } T=\{(x_1, y_1),(x_2, y_2),\cdots,(x_n, y_n)\} T={(x1​,y1​),(x2​,y2​),⋯,(xn​,yn​)}
其中， x i ∈ R p , y ∈ Y = { − 1 , 1 } , i = 1 , 2 , ⋯   , n x_i\in R^p,y\in Y=\{-1,1\},i=1,2,\cdots,n xi​∈Rp,y∈Y={−1,1},i=1,2,⋯,n，并且假设有样本集线性可分。
设有分离超平面：
$$w^{T}x+b=0$$
使得样本集被分成正负两部分。
以及分类决策函数：
$$f(x)=sign(w^{T}x+b)$$
并有$w^{T}x+b>0$时，为正类；$w^T+b<0$时，为负类。

很自然的，我们只需要：
$$y_i(w^T{x}_i+b)>0$$
对每个样本$(x_i,y_i)$成立即可。
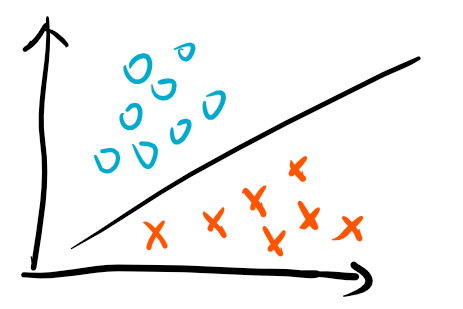
但这存在一个问题，考虑下面一个例子：

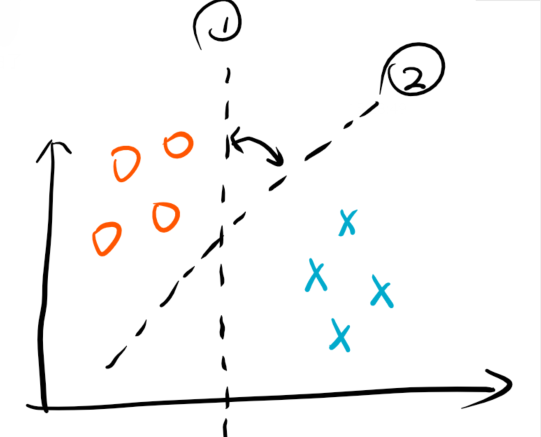
可以发现，满足上面条件的超平面有无穷多个。但是从样本点来看，是存在一个相比较而言更加好的一个超平面，那么就是处于$H_1,H_2$中间的超平面，而SVM正是可以求解这个最优超平面的算法。

算法

Functional/Geometric Margin

首先介绍两个概念：
函数间隔(functional margin):
$${\hat{\gamma }}_i=y_i(w^T{x}_i+b)$$
假如，我们已经求解得到最优超平面，即是有$w,b$。但是，实际上$\lambda w,\lambda b$也同样为那个最优超平面的系数。因此，首先，基于这一点，函数间隔只能描述相对大小；其二，为了解决这个多解问题，我们应该引入一些限制条件，比如$||w||=1$，进行归一化。而为了不受$w,b$的成倍变化带来的大小变化，我们引入几何间隔。
几何间隔(geometric margin):
$${\gamma }_i=\frac{y_i(w^T{x}_i+b)}{||w||}$$
注意：上述距离一般为，带符号的距离(signed distance)，而当样本点被正确分类时，那么就成为样本点到超平面的距离。

硬间隔最大化

SVM的间隔最大化思想就是，找到$w,b$使得，距离超平面最近的那个点，其到超平面的距离最大。基于这个想法，我们有：
$$\begin{array}{rl}& \underset{w,b}{\max }\underset{i}{\min }{\gamma }_i\\ & s.t.y_i(w^T{x}_i+b)>0,i=1,2,\cdots ,n\\ 又:& \\ & {\gamma }_i=\frac{y_i(w^T{x}_i+b)}{||w||}\\ 有:& \\ & \underset{w,b}{\max }\underset{i}{\min }\frac{y_i(w^T{x}_i+b)}{||w||}\\ & =\underset{w,b}{\max }\frac{1}{||w||}\underset{i}{\min }{y}_i(w^T{x}_i+b)\end{array}$$

又由上文分析，$y_i(w^T{x}_i+b)={\hat{\gamma }}_i$可以被任意放缩，那么：
$$\begin{array}{rl}令：& \\ & \underset{i}{\min }{\hat{\gamma }}_i=1\\ 问题转化为：& \\ & \underset{w,b}{\max }\frac{1}{||w||}\\ & s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2,\cdots ,n\\ 也即是:& \\ & \underset{w,b}{\min }\frac{1}{2}{w}^{T}w\\ & s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2,\cdots ,n\end{array}$$

对偶算法

拉格朗日函数

通过上文的分析，我们得到目标函数和限制条件：
$$\begin{array}{rl}& \underset{w,b}{\min }\frac{1}{2}{w}^{T}w\\ & s.t.1-y_i(w^T{x}_i+b)\le 0,i=1,2,\cdots ,n\end{array}$$
很自然的，我们想到构造拉格朗日函数，有：
$$\begin{array}{rl}& \mathcal{L}(w,b,{\lambda }_i)=\frac{1}{2}{w}^{T}w+\sum _i^n{\lambda }_i(1-y_i(w^T{x}_i+b))\\ & s.t{\lambda }_i\ge 0\end{array}$$
此时，问题就变成了,无约束的优化问题：
$$\begin{array}{rl}\underset{w,b}{\min }\underset{{\lambda }_i}{\max }& \mathcal{L}(w,b,{\lambda }_i)=\frac{1}{2}{w}^{T}w+\sum _i^n{\lambda }_i(1-y_i(w^T{x}_i+b))\\ & s.t{\lambda }_i\ge 0\end{array}$$

对偶转换

由拉格朗日的对偶性，我们可以知，上述问题可以转换为：
$$\begin{array}{rl}\underset{{\lambda }_i}{\max }\underset{w,b}{\min }& \mathcal{L}(w,b,{\lambda }_i)=\frac{1}{2}{w}^{T}w+\sum _i^n{\lambda }_i(1-y_i(w^T{x}_i+b))\\ & s.t{\lambda }_i\ge 0\end{array}$$
关于为什么要进行对偶转换，原因有两点：1.更容易求解。2.自然引入核函数，进来推广到非线性空间。

对偶问题证明

please jump：SVM对偶问题

对偶问题的求解

由上文可知对偶问题为：
$$\begin{array}{rl}\underset{{\lambda }_i}{\max }\underset{w,b}{\min }& \mathcal{L}(w,b,{\lambda }_i)=\frac{1}{2}{w}^{T}w+\sum _i^n{\lambda }_i(1-y_i(w^T{x}_i+b))\\ & s.t{\lambda }_i\ge 0\end{array}$$
现在就来求解$w,b$：
先看min部分：
$$\begin{array}{rl}& \underset{w,b}{\min }\mathcal{L}(w,b)=\frac{1}{2}{w}^{T}w+\sum _i^n{\lambda }_i(1-y_i(w^T{x}_i+b))\\ & =\frac{1}{2}{w}^{T}w+\sum _i^n{\lambda }_i-\sum _i^n{\lambda }_i{y}_i(w^T{x}_i+b))\\ & \frac{\partial L(w,b)}{\partial b}=-\sum _i^n{\lambda }_i{y}_i=0\\ & \frac{\partial L(w,b)}{\partial w}=w-\sum _i^n{\lambda }_i{y}_i{x}_i=0\\ 综上有：& \\ & \sum _i^n{\lambda }_i{y}_i=0\\ & w=\sum _i^n{\lambda }_i{y}_i{x}_i\\ 代入对偶问题有：& \\ & \underset{{\lambda }_i}{\max }\mathcal{L}({\lambda }_i)=\frac{1}{2}(\sum _i^n{\lambda }_i{y}_i{x}_i{)}^T(\sum _i^n{\lambda }_i{y}_i{x}_i)+\sum _i^n{\lambda }_i-\sum _i^n{\lambda }_i{y}_i(w^T{x}_i+b)\\ & =\frac{1}{2}(\sum _i^n{\lambda }_i{y}_i{x}_i{)}^T(\sum _j^n{\lambda }_j{y}_j{x}_j)+\sum _i^n{\lambda }_i-\sum _i^n{\lambda }_i{y}_i((\sum _j^n{\lambda }_j{y}_j{x}_j{)}^T{x}_i)\\ & -\sum _i^n{\lambda }_i{y}_{i}b\\ & =\frac{1}{2}\sum _i^n\sum _j^n({\lambda }_i{y}_i{x}_i{)}^T{\lambda }_j{y}_j{x}_j-\sum _i^n\sum _j^n{\lambda }_i{y}_i({\lambda }_j{y}_j{x}_j{)}^T{x}_i+\sum _i^n{\lambda }_i\\ & =\frac{1}{2}\sum _i^n\sum _j^n({\lambda }_i{\lambda }_j{y}_i{y}_j)x_i^T{x}_j-\sum _i^n\sum _j^n({\lambda }_i{\lambda }_j{y}_i{y}_j)x_j^T{x}_i+\sum _i^n{\lambda }_i\\ & 又x_j^T{x}_i=x_i^T{x}_j\\ & =-\frac{1}{2}\sum _i^n\sum _j^n({\lambda }_i{\lambda }_j{y}_i{y}_j)x_i^T{x}_j+\sum _i^n{\lambda }_i\end{array}$$
综上，max部分为：
$$\underset{{\lambda }_i}{\max }\mathcal{L}({\lambda }_i)=-\frac{1}{2}\sum _i^n\sum _j^n({\lambda }_i{\lambda }_j{y}_i{y}_j)x_i^T{x}_j+\sum _i^n{\lambda }_i$$
即是：
$$\begin{array}{rl}& \underset{{\lambda }_i}{\min }\mathcal{L}({\lambda }_i)=\frac{1}{2}\sum _i^n\sum _j^n({\lambda }_i{\lambda }_j{y}_i{y}_j)x_i^T{x}_j-\sum _i^n{\lambda }_i\\ & s.t.{\lambda }_i\ge 0\\ & \sum _i^n{\lambda }_i{y}_i=0\end{array}$$
假设求得：${\lambda }^{\ast }=({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)$，那么只需要带入${\sum }_i^n{\lambda }_i{y}_i{x}_i$，即可解得$w^{\ast }$，又通过$w{{}^{\ast }}^T{x}_i+b=1,{\lambda }_i\ge 0$，即可解得$b^{\ast }$。此时$x_i$也被称为支持向量(support vector)。

软间隔最大化

在实际的数据集中，总会存在着噪点(noise)，或者离群点(outlier)。考虑下图：

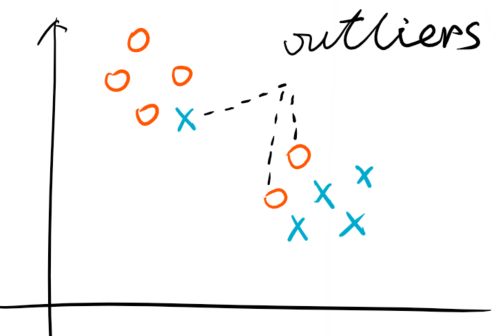
那么显然，这个已经无法简单用一个超平面来解决问题了。面对这样的情况，我们有三个方法，原始数据层面，我们可以做数据清洗，或者特征工程。二是利用非线性模型（实际上，在这里用非线性模型过于大材小用，或者不合理。因为这显然是一个线性可分，但是存在噪点的数据集）。第三个办法就是，允许我们SVM模型可以进行误分类。即是说上文的：
$$y_i(w^T{x}_i+b)\ge 1,i=1,2,\cdots ,n$$
可以对部分样本不成立。那么问题就在于如果巧妙的将允许犯错加入到SVM模型中。

合页损失函数（hinge loss function）

由于有些样本会导致：
$$y_i(w^T{x}_i+b)<1,i=1,2,\cdots ,n$$
很自然的，我们就希望能纠正这一点，若犯错，需纠正数值为：
$$\Delta =1-y_i(w^T{x}_i+b),given{y}_i(w^T{x}_i+b)<1$$
从而使得：
$$y_i(w^T{x}_i+b)+\Delta \ge 1,given{y}_i(w^T{x}_i+b)<1$$
下面给出合页损失函数的定义：
ξ i = m a x { 0 , 1 − y i ( w T x i + b ) } \xi_i=max\{0,1-y_i(w^Tx_i+b)\} ξi​=max{0,1−yi​(wTxi​+b)}
同样使得：
$$y_i(w^T{x}_i+b)+{\xi }_i\ge 1$$
如果我们令：$y_i(w^T{x}_i+b)=z$，那么$f(z)$的图像则为：

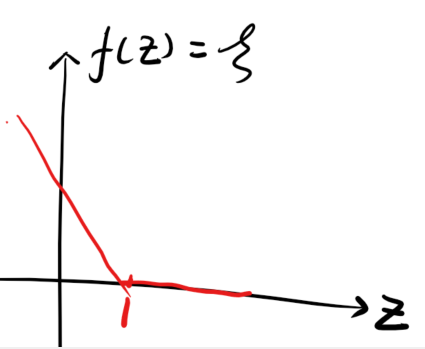
从硬到软（原始问题）

由上文知，硬间隔的原始问题：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}{w}^{T}w \\ s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2,\cdots ,n \end{gathered}$$
又由上文的分析，限制条件变更为:
$$s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i,i=1,2,\cdots ,n$$
但是只这样子做，会存在一个问题，因为我们对${\xi }_i$所作出的犯错修正没有作出任何限制。因而，模型为了使得最小间隔尽量的大，而进行任意的犯错修正，最终导致误分类点很多。因此，我们需要对${\xi }_i$的修正行为，进行限制。那么很自然的，考虑到，修正行为的强度和修正值成正比，因而，我们将${\xi }_i$的值作为损失的角色，加入到${\min }_{w,b}\frac{1}{2}{w}^{T}w$中，最终得到软间隔的原始问题：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}{w}^{T}w+C\sum _i^n{\xi }_i \\ s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i,i=1,2,\cdots ,n \end{gathered}$$
最终，软间隔成为一方面使得$\min \frac{1}{2}{w}^{T}w$，即最小间隔最大，一方面使得$\min C{\sum }_i^n{\xi }_i$，即误分类点尽量少。其中$C$是调和两者的系数。

软间隔的对偶问题

其与硬间隔的对偶问题相似，就略了。

线性不可分SVM

核方法

Driving Example

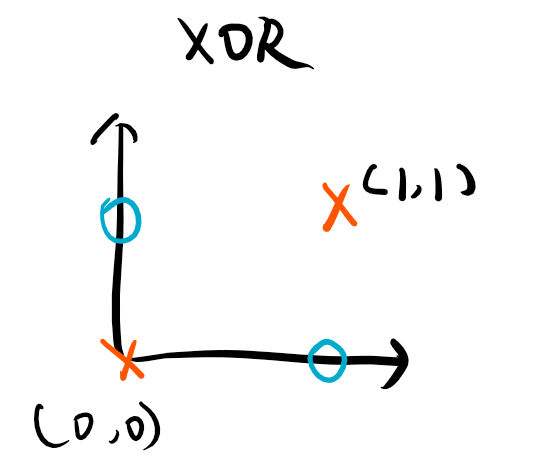
考虑下面两个例子：
1.同维度映射

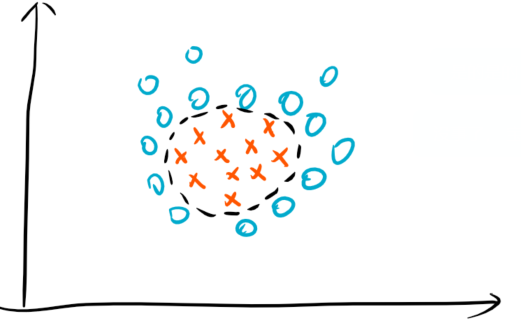
很直观的可以看出来，这对于线性SVM来说，是“十二月天找杨梅”。因此，我们只能通过某种非线性映射将样本点映射到新的空间，比如下图：

上面的映射相当于，从输入空间$\mathbf{x}=(x_1,x_2)$通过$\varphi (\mathbf{x})$映射到了$\mathbf{x}=(x_1^2,x_2^2)$
2.高维映射

考虑使用如下的映射：$\varphi (\mathbf{x})=(x_1,x_2,(x_1-x_2{)}^2)$，得到：

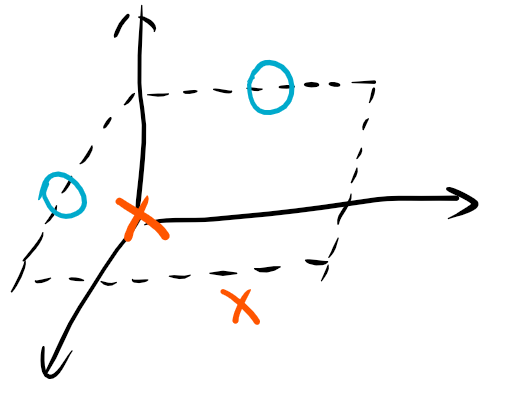
从而变得线性可分。

核技巧

由上文可知，我们求解SVM的时候最后一步化简有：
$$\underset{{\lambda }_i}{\min }\mathcal{L}({\lambda }_i)=\frac{1}{2}\sum _i^n\sum _j^n({\lambda }_i{\lambda }_j{y}_i{y}_j)x_i^T{x}_j-\sum _i^n{\lambda }_i$$
注意到其中有，$x_i^T{x}_j$，这是我们需要计算的，那么如果我们进行了映射，式子就变为$\varphi (x_i)\cdot \varphi (x_j),\cdot 为内积$。这时计算它就变为，先找到映射$\varphi (x)$，再计算内积。那么我们是否可以找到一个函数一步达到目的呢，核技巧需要用到的核函数就诞生了。

核函数

定义

设$\mathcal{X}$为输入空间，$\mathcal{H}$为特征空间，并且有映射：
$$\varphi (x):\mathcal{X}->\mathcal{H}$$
而核函数满足有：
$$K(x,z)=\varphi (x)\cdot \varphi (z)x,z\in \mathcal{X}$$
因而上式
$$\underset{{\lambda }_i}{\min }\mathcal{L}({\lambda }_i)=\frac{1}{2}\sum _i^n\sum _j^n({\lambda }_i{\lambda }_j{y}_i{y}_j)x_i^T{x}_j-\sum _i^n{\lambda }_i$$
则变为
$$\underset{{\lambda }_i}{\min }\mathcal{L}({\lambda }_i)=\frac{1}{2}\sum _i^n\sum _j^n({\lambda }_i{\lambda }_j{y}_i{y}_j)K(x,z)-\sum _i^n{\lambda }_i$$

正定核

首先明确一点说，没有特殊说明，那么核函数指的就是正定核函数。
那么满足什么条件的函数才能被称为核函数$K(x,z)$呢。

希尔伯特(Hilbert space)空间

如果函数$K(x,z)$是定义在$\mathcal{X}\times \mathcal{X}$上的对称函数，并且对任意的$x_1,x_2\cdots ,x_m\in \mathcal{X},K(x,z)$关于$x_1,x_2,\cdots ,x_m$的Gram矩阵是半正定的。那么，我们可以根据函数$K(x,z)$构成一个具有内积性质的希尔伯特空间。
空间构造过程略。

正定核的充要条件

必要性：
即已知为正定核，证明其为对称函数，且Gram矩阵为半正定。

对称性：
由正定核定义可得：
$$K(x,z)=\varphi (x)\cdot \varphi (z)$$
由内积对称性：
$$K(x,z)=\varphi (z)\cdot \varphi (x)=K(z,x)$$
因此，其为对称函数。

半正定性：
对于任意$x_1,x_2,\cdots ,x_m$,构造$K(x,z)$关于$x_1,x_2,\cdots ,x_m$的Gram矩阵：
$$[K_{ij}{]}_{m\times m}=[K(x_i,x_j){]}_{m\times m}$$
若要证明其半正定性，那么由定义只需证明：
$$对于任意\alpha \in {\mathbb{R}}^m,{\alpha }^T[K_{ij}{]}_{m\times m}\alpha \ge 0$$
展开有:
$$\begin{array}{rl}& \left[\begin{array}{c}{\alpha }_1{\alpha }_2\cdots {\alpha }_m\end{array}\right]\left[\begin{array}{cccc}{K}_{11}& K_{12}& \cdots & K_{1m}\\ K_{21}& K_{22}& \cdots & K_{2m}\\ ⋮& ⋮& ⋮& ⋮\\ K_{m1}& K_{m2}& \cdots & K_{mm}\end{array}\right]\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_m\end{array}\right]\\ & =\sum _i^m\sum _j^m{\alpha }_i{\alpha }_j{K}_{ij}\\ & =\sum _i^m\sum _j^m{\alpha }_i{\alpha }_j\varphi (x_i{)}^T\varphi (x_j)\\ & =\sum _i^m{\alpha }_i\varphi (x_i{)}^T\sum _j^m{\alpha }_j\varphi (x_j)\\ & =<\sum _i^m{\alpha }_i\varphi (x_i),\sum _j^m{\alpha }_j\varphi (x_j)>\\ & =||\sum _i^m{\alpha }_i\varphi (x_i)|{|}^2\ge 0\end{array}$$
因此是核函数则满足：1.对称性 2.Gram矩阵为半正定
充要性（待续）