ML_NOTES_P10

P10

分类问题：什么是分类问题，如何利用朴素贝叶斯公式来做分类。以及如何从朴素贝叶斯公式推导出感知机模型（两个之间的联系）

什么是分类问题？

要做分类我们第一件事要做的就是把实物数值化，用具体的数字来代替某一个特征。比如在宝可梦中把攻击力和防御力具体化，攻击力为5，防御力为10。把这些特征组成一个向量我们就可以得到一组用来代替这个事物的特征向量。

现在我们得到特征向量了，把这组特征向量输入到模型中，模型输出一个代表分类的结果。比如我们现在将宝可梦分为两个类别一类是水系一类是一般系。现在我们有一只不知属性的宝可梦知道他的一组组特征向量为（5，5）攻击力5，防御力5，（特征不止一个，我们用两个来举例子）我们需要根据他的特征向量将其分到水系或者一般系中。

朴素贝叶斯公式如何解决分类问题？

以二分类为例

先来看最熟悉的贝叶斯公式：如图所示有两个盒子盒子1和盒子2，盒子里面分别有蓝球和绿球。现在我们拿到一个蓝球求这个蓝球来自盒子1和盒子2的概率分别是多少？

求这个概率我们需要知道拿到盒子1和盒子2的概率分别是多少即 $p(c_1)$ 和 $p(c_2)$ 以及蓝球在盒子1，2中出现的概率分别是多少即 $p(x|c_1)$ 和 $p(x|c_2)$

根据贝叶斯公式 (1) 即可求得蓝球来自盒子1和盒子2的概率 (分母为全概率公式)

$$p(c1|x)=\frac{p(x|c_1)p(c_1)}{p(x|c_1)p(c_1)+p(x|c_2)p(c_2)}\text{\hspace{1em}(1)}$$

现在来看下贝叶斯公式和分类之间的联系。我们根据公式求得了蓝球来自盒子1，2的概率，如果 $p(c_1|x)$ 大于0.5则认为来自盒子1。同理可得 p(c2|x) 大于0.5则认为蓝球来自盒子2。现在我们把他换位宝可梦属性分类问题。盒子1，2对应宝可梦的两种属性（水系，一般系）。里面的球代表特征，现在我们拿到一个特征向量为（5，5）的宝可梦，我们需要判断他是哪一个类别的。我们需要知道训练集中宝可梦水系的概率 $p(c_1)$ 和一般系的概率 $p(c_2)$ 以及特征向量（5，5）在水系中和一般系中出现的概率 $p(x|c_1)$ 和 $p(x|c_2)$。现在我们将知道的这几个概率带入贝叶斯公式求出概率即可。

现在的问题是我们怎么知道 $p(c_1),p(c_2),p(x|c_1),p(x|c_2)$ ? 其中$p(x|c1),p(x|c_2)$ 叫做似然概率， $p(c_1),p(c_2)$ 叫做先验 prior。

假设现在我们现在有100个已知属性和特征向量的宝可梦训练集，其中水系的有50只，一般系的50只，那我们现在就有了 $p(c_1)=0.5,p(c_2)=0.5$ 。现在如何求得 $p(x|c_1),p(x|c_2)$ ? 即在水系和一般系中已知的50只宝可梦的特征向量分别求得特征向量（5，5）出现的概率。拿水系来举例 即求$p(c_1|x)$ 。我们其实可以知道现在的训练集中的50只水系宝可梦只是水系中的一部分还有很多其他未知的水系宝可梦，这50个只是正好采样时采到了他们。假设宝可梦的特征是从高斯分布（你也可以假设你喜欢的Probability distribution概率分布函数，如果你选择的分布函数较简单（参数量少）那你的bias就大，variance就小.可以用data set来判断一下用什么样的probability distribution作为model是比较好的）中采样得到的。那我们怎么知道是从那个高斯分布上采样得到的呢？因为不同的高斯分布也有可能采样时采到这50个宝可梦，怎么得到这个Gaussian的均值和方差呢？这里用到的思想是极大似然估计。把这50只宝可梦的数据分布作为整个水系宝可梦的数据分布，根据已知的50只宝可梦求得这50条数据的均值和方差作为我们的高斯分布的均值和方差。现在求得了水系宝可梦的分布就可以求得数据（5，5）在这个分布上sample（采样）出来的概率即求得了 p(c_1|x)。同理可求 p(c_2|x)。将这4个概率带回朴素贝叶斯公式就可以得到（5，5）最有可能是哪一个类别的宝可梦。问题得到解决。😄

如何从朴素贝叶斯推出感知机模型？

在刚刚的公式中我们需要找的高斯函数的分布$（u,sigma）$就是我们要找的参数，不同的值对应不同的模型，我们要在所有的值中找到最有可能的值（用的方法是极大似然估计）。刚刚的公式中我们每个类别的高斯分布均值和协方差都是独立不同的 $u_1\ne u_2,sigm{a}_1\ne simg{a}_2$。这样得到的效果往往不太好 😞 ，常用的方法是不同类别之间共用一个covariance matrix（协方差矩阵）为什么共用一个协方差矩阵效果较好见补充。

这个时候的协方差矩阵为原来两个的加权 $$simga=a\ast sigm{a}_1+b\ast sigm{a}_2$$ a,b也是根据极大似然估计算出来的。$a=p(c_1),b=p(c_2)$ 。

在两个类别共用一个协方差的基础上我们将朴素贝叶斯公式进行一些数学推导变形为感知机模型，下面就是见证奇迹的时刻🐵

在朴素贝叶斯公式中上下同除以分子，令 $z=ln\frac{p(x|c_1)p(c_1)}{p(x|c_2)p(c_2)}$ ,则原式就等于$p(c_1|x)=\frac{1}{1+e^{-z}}$ 即为已知的函数sigmoid

接下来看下这个sigmoid 化简之后是什么？

经过上面一系列的数学公式化简最后得到了$P(C_1|x)=\sigma (w\cdot x+b)$ 所以我们找了半天的先验，假设数据的分布，最后我们要找的就是两个常数w,b。

看不懂上面一系列推导的看李宏毅老师的机器学习P09最后的推导部分

补充

什么是高斯分布？

高斯分布也叫做正太分布，若有一堆数据(一个变量)满足公式 2则称这堆数据的分布满足均值为$u$,方差为 ${\sigma }^2$的高斯分布。上式公式就是我们常见的一元高斯分布。均值为0方差为1的高斯分布叫做标准正太分布。

$$f(x)=\frac{1}{\sigma \sqrt{2\pi }}\cdot e^{-\frac{1}{2}\cdot (\frac{x-u}{\sigma }{)}^2}\text{\hspace{1em}(2)}$$

现在我们将高斯分布扩展到多维空间即假设有多个变量并且假设他们之间相互独立，则独立的n元高斯分布如公式3

$$f_{u,\Sigma }(x)=\frac{1}{(2\pi {)}^{\frac{D}{2}}}\frac{1}{|\Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(x-u{)}^T{\Sigma }^{-1}(x-u)}\text{\hspace{1em}(3)}$$

其中\Sigma为变量x的协方差矩阵 i行,g列的元素值表示x_i,x_j的协方差（表示两个变量之间的相关性）。由此可知\Sigma为一个关于对角线对称的矩阵（x_i,x_j和x_j,x_i是一样的）。由于我们现在假设变量之间相互独立，所以除对角线以外的值全为0
$$\Sigma =\begin{array}{cccc}{\sigma }_1^2& 0& \cdots & 0\\ 0& {\sigma }_1^2& \cdots & 0\\ ⋮& \cdots & \cdots & ⋮\\ 0& 0& \cdots & {\sigma }_1^2\end{array}\text{\hspace{1em}(4)}$$
当数据之间不独立的时候
$$\Sigma =\begin{array}{cccc}V(X_1)& Cov(X_1,X_2)& \cdots & Cov(X_1,X_D)\\ Cov(X_2,X_1)& V(X_2)& \cdots & Cov(X_2,X_D)\\ \cdots & \cdots & \cdots & \cdots \\ Cov(X_D,X_1)& Cov(X_D,X_2)& \cdots & V(X_D)\end{array}\text{\hspace{1em}(5)}$$
比如现在我们讨论两个参数的高斯分布,下图为不同的均值和方差的高斯分布图投影到二维平面的等高线图。

二维图	投影之后的平面图

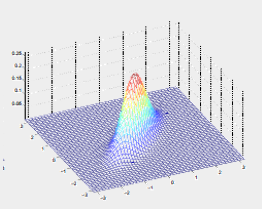投影到二维平面的等高线图

那我们怎么知道是什么样的高斯分布可以使得P最大呢，怎么求解呢？

实际上就是该事件发生的概率就等于每个点都发生的概率之积，我们只需要把每一个点的data代进去，就可以得到一个关于u和$\Sigma$的函数，分别求偏导，解出微分是0的点，即使L最大的那组参数，便是最终的估测值，通过微分得到的高斯函数的$u$和$\Sigma$的最优解如下： $$u^{\ast },Sigm{a}^{\ast }=\arg \underset{u,\Sigma }{\max }L(u,\Sigma )u^{\ast }=\frac{1}{10}\sum _{n=1}^{10}{x}^n{\Sigma }^{\ast }=\frac{1}{10}\sum _{n=1}^{10}(x^n-u^{\ast })(x^n-u^{\ast }{)}^T.$$ 当然如果你不愿意去现场求微分的话，这也可以当做公式来记忆(u^{*刚好是这堆数据的数学期望，\Sigma}*刚好是协方差)

注：数学期望：$u=E(X)$，协方差：$\Sigma =cov(X,Y)=E[(X-u)(Y-u{)}^T]$，对同一个变量来说，协方差为$cov(X,X)=E[(X-u)(X-u)^T $

什么是极大似然估计？

假设我们现在有一个特征共有10条数据（十个样本点）是由某个高斯分布采样出来的，那怎么确定这十个点是来自怎样的高斯分布呢？实际上不管参数是什么的高斯分布都可以采样出这十个样本点，只是可能性的问题，我们现在假设采样出第i个样本的概率为$P(X_i)$ ，采样出每个样本点的可能性是独立的，那么采样出这10个样本的概率 $P={\Sigma }_1^{10}P(X_i)$当有一组$u,{\sigma }^2$ 使得概率P最大的时候我们就认为这10个样本就是来自这个使得P 最大的高斯分布（用已知的部分数据去估计全部数据的分布）。那有没有可能这10个点来自其他分布呢？完全有可能啊，当这10个点是被某个别有用心的人专门挑选的不具代表性的特殊的点这个时候完全有可能使得P最大的分布不是数据的整体分布。但是极大似然估计才不管这些，只要你这个高斯分布使得P最大了那我就认为你是采样自这个高斯分布的。这个时候极大似然估计就歇菜了啊估计错了啊公式里面的贝叶斯里面的似然概率都估计错了模型训练出来的结果能好吗？所以为了防止这种情况我们的采样点要尽量是能够代表整体分布的，既然你诚心的发问了怎么保证我们采样出来的点能够代表整体分布呢？采取的措施是采样的时候做到随机采样，采取尽可能多的数据保证数据的泛化性。

怎么通俗的理解极大似然估计呢？一句话总结就是看起来是那么回事我们就认为是那么回事。打个比分，我们在街上看见看见一个女的牵着一个小女孩的手，并且他们两个长得很想，还穿着亲子装。我们根据这些信息推测出他们两个是母女关系。

为什么不同类别共用一个covariance matrix效果是比较好的?😐

协方差矩阵 $\Sigma$ 表示的是各变量之间关系的矩阵，矩阵的 i行,g列的元素值表示$x_i,x_j$的协方差（表示两个变量之间的相关性）。
$$\Sigma =\begin{array}{cccc}V(X_1)& Cov(X_1,X_2)& \cdots & Cov(X_1,X_D)\\ Cov(X_2,X_1)& V(X_2)& \cdots & Cov(X_2,X_D)\\ \cdots & \cdots & \cdots & \cdots \\ Cov(X_D,X_1)& Cov(X_D,X_2)& \cdots & V(X_D)\end{array}\text{\hspace{1em}(6)}$$
由于数据之间大多是具有相关性的（不独立），当特征（变量）很多的时候这个矩阵会很大（和input的feature size的平方成正比），当不同类别给不同协方差的时候会造成模型的参数太多从而导致模型方差过大出现过拟合，当不同类别共用一个协方差的时候可以有效减少参数量。（参数不是越多越好，找100个不相干的特征不如10个关键特征）。