《机器学习by周志华》学习笔记-线性模型-03

1、多分类学习

1.1、背景

我们在上一节介绍了「线性判别分析（LDA）」，LDA的从二分类任务可以推广到多分类任务中。

而现实中常遇到的多分类学习任务。有些二分类的学习方法可以直接推广到多分类，但是更多情况下是基于一些策略，利用二分类学习器来解决多分类的问题。

1.2、概念

我们通常将「分类学习器」简称「分类器（classifier）」，多个「分类器」的集成使用，则称为「集成学习」。

一般的，分类器使用「多分类学习」的方法来完成分类任务。本章主要介绍了「多分类学习」的方法。

1.3、基本思路

「多分类学习」的基本思路是「拆解法」，即将「多分类任务」拆成「若干个二分类任务」求解。

具体来说就是：

• 先对问题进行拆分；
• 然后为「拆出的每个二分类任务」训练出一个「分类器」；
• 最后对这些分类器进行「集成使用」；

在测试时，对这些分类器的预测结果进行集成，获得最终的多分类结果。这里的关键如下：

• 如何对多分类任务进行拆分
• 如何对多个分类器进行集成

1.4、拆分策略

给定m个示例的数据集D有n个类别,y是其所有示例的真实标记，所有类别集合用C表示，则：

常见的拆分策略有三种：

• 一对一（One vs.One，简称OvO）
• 一对其余（One vs.Rest，简称OvR）：亦称OvA(One vs.All)，但OvA这个说法不严格，因为不可能把“所有类”作为反类。
• 多对多（Many vs.Many，简称MvM）

后面我们将详细介绍这三种拆分策略。

1.4.1、一对一（OvO）

首先，将n个类别「两两配对」，从而产生个二分类任务，即个二分类器。

其次，每个二分类任务，都表示正例，表示反例。

再次，将的所有m个样本同时提交给个二分类器。

最后，结果通过投票产生，即把被预测的最多的类别作为最终分类结果。

如下图所示：

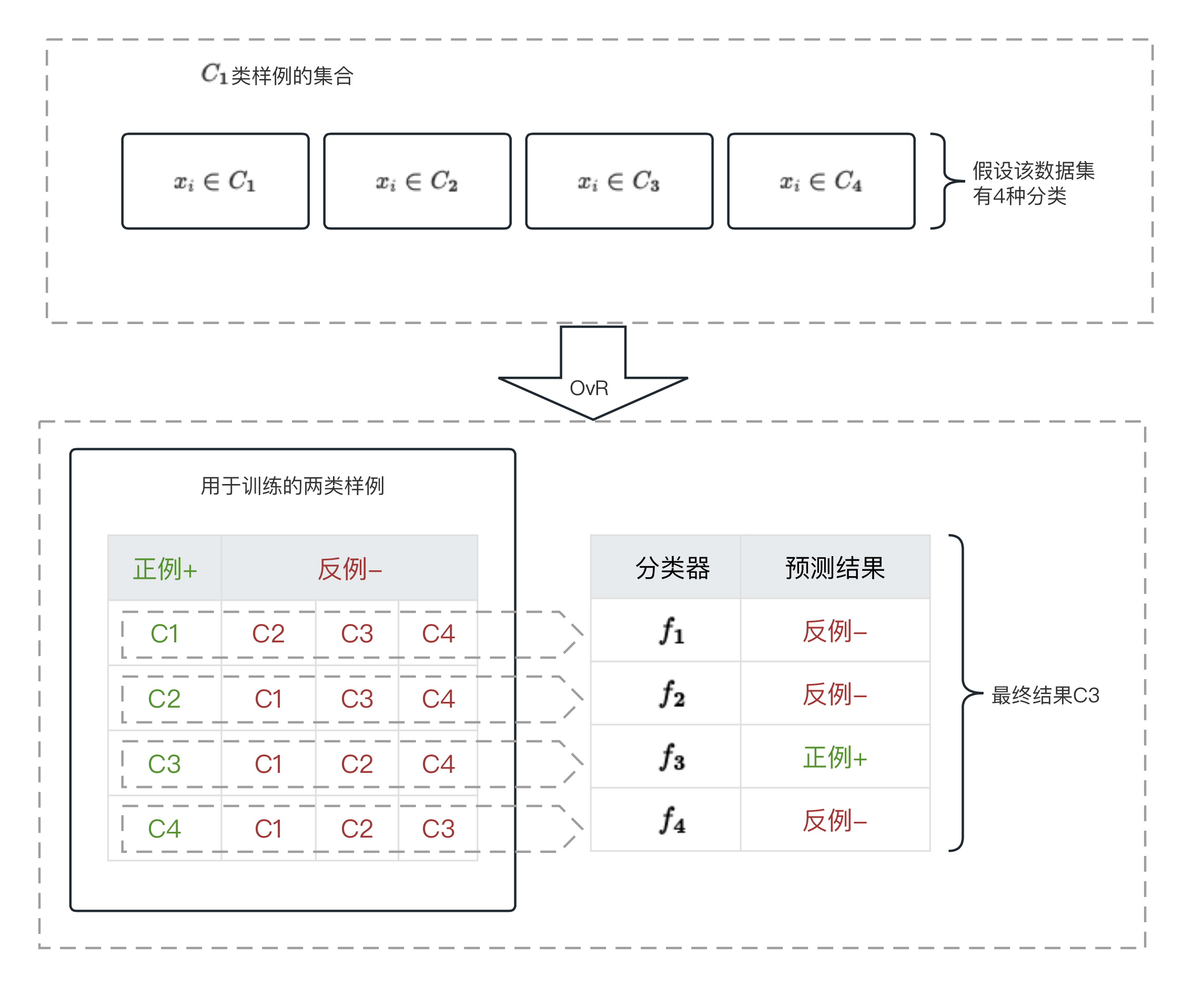
1.4.2、一对其余（OvR）

首先，每次将一个类的样例作为正例、其余的类作为反例来训练，从而产生n次训练任务、n个二分类器以及预测结果。

其次，将D的所有m个样本同时提交给个二分类器。

最后，分情况选择分类结果：

• 当只有一个分类器预测为正例，则对应类别就是分类结果，例如下图的C3
• 当有多个分类器预测为正例，则考虑每个分类器预测的置信度，选择最大的类别作为分类结果。

OvO与OvR对比：

对比类别	OvO	OvR	分析
训练分类器个数	n	n(n-1)/2	OvO的存储开销、测试（训练）时间较大。
每个分类器训练样例数	2个类别的样例	n个类别的样例	在类别很多的时候，OvO的测试（训练）时间、开销更小。
预测性能	/	/	依赖于二者的数据分布，多数情况都差不多。

1.4.3、多对多（MvM）

就是将若干个类的样例作为「正例」，其他类的样例作为「反例」。其构造必须有特殊的设计，不能随意选取。

OvO和OvR是MvM的一种拆分方式，属于MvM的特例。

我们会在下面介绍一种常用的选取技术「纠错输出码（Error Correcting Output Codes，简称ECOC）」，它是将编码的思维引入类别拆分，并尽可能在编码过程中具有容错性，其工作主要分为以下2步：

第一步：编码

• 对n个类别做m次划分，每次划分将一部分类别划分为「正类」，另一部分为「反类」，从而形成一个二分类训练集。
• 一共产生m个训练