旅行商问题,即TSP问题(Traveling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
首先可以去下载数据集https://download.csdn.net/download/viafcccy/11273100(支持博主一点下载积分 也可以直接使用下方的数据),接下来将使用数据集中的数据进行分析
31.2006990000000 121.195447000000
31.1999740000000 121.302863000000
31.2487390000000 121.345995000000
31.1737900000000 121.128212000000
31.1610230000000 121.111884000000
31.1522860000000 121.187403000000
31.1651130000000 121.110473000000
31.3111830000000 121.545410000000
31.2569610000000 121.473418000000
31.2618510000000 121.544265000000
31.2644080000000 121.412710000000
31.2800750000000 121.434740000000
31.2330560000000 121.372183000000
31.2372000000000 121.402512000000
31.2820830000000 121.538396000000
31.2116730000000 121.389858000000
31.3179770000000 121.553050000000
31.2645010000000 121.355632000000
31.3125730000000 121.472295000000
31.3521800000000 121.437859000000
31.4014200000000 121.464019000000
31.4050720000000 121.509817000000
31.3203530000000 121.474440000000
31.4829720000000 121.332108000000
31.4111360000000 121.353557000000
31.3571250000000 121.507167000000
31.3613660000000 121.392618000000
31.3162110000000 121.405014000000
31.3333740000000 121.462548000000
31.2942450000000 121.311899000000
31.3978140000000 121.281854000000
31.3040400000000 121.174793000000
31.3306560000000 121.271897000000
31.2535280000000 121.312014000000
31.1189280000000 121.430417000000
31.1656120000000 121.457527000000
31.1659440000000 121.399218000000
31.2781040000000 121.695219000000
31.2491910000000 121.683054000000
31.2665760000000 121.584458000000
30.9059200000000 121.629400000000
31.2151300000000 121.653498000000
31.0331490000000 121.585322000000
30.9320060000000 121.569712000000
31.0516380000000 121.597918000000
31.0331510000000 121.194807000000
31.0534760000000 121.458736000000
31.0886080000000 121.376303000000
31.2080200000000 121.547540000000
31.1606670000000 121.512126000000
31.1796280000000 121.523585000000
31.1344450000000 121.510146000000
31.2121040000000 121.370803000000
31.1752590000000 121.286866000000
31.2503750000000 121.241234000000
31.2682660000000 121.494618000000
31.2859420000000 121.355885000000
31.2765840000000 121.388417000000
30.9391320000000 121.458801000000
30.9257390000000 121.518067000000
30.7270350000000 121.359077000000
30.7310450000000 121.339345000000
30.9261900000000 121.445795000000
30.8990280000000 121.179453000000
30.8373880000000 121.186939000000
30.8782630000000 121.559792000000
30.8592860000000 121.342500000000
30.9284320000000 121.472888000000
31.3121450000000 121.477937000000
31.3489050000000 121.479111000000
31.3568480000000 121.360833000000
31.3349670000000 121.503255000000
31.4027060000000 121.275040000000
31.3738950000000 121.240109000000
31.2904340000000 121.317538000000
31.3840390000000 121.153913000000
31.2801720000000 121.303692000000
31.1152880000000 121.422746000000
31.1802720000000 121.421049000000
31.1431390000000 121.433062000000
31.2014330000000 121.434782000000
31.1460100000000 121.362961000000
31.1907530000000 121.372918000000
31.1471410000000 121.402742000000
31.1864050000000 121.457014000000
31.1834800000000 121.434396000000
31.1259040000000 121.423424000000
31.2780920000000 121.597586000000
31.2648240000000 121.566820000000
31.3353140000000 121.581277000000
31.2804130000000 121.593315000000
31.2718620000000 121.593569000000
31.2811240000000 121.616186000000
31.3466450000000 121.592160000000
31.2837010000000 121.595378000000
31.2694150000000 121.592652000000
31.0477240000000 121.783712000000
31.0307480000000 121.655021000000
31.2011960000000 121.634969000000
31.0623070000000 121.774891000000
30.9123690000000 121.655509000000
31.2660750000000 121.685597000000
31.2366290000000 121.732530000000
31.0185560000000 121.437335000000
31.0551430000000 121.408290000000
31.0524320000000 121.415297000000
31.0948100000000 121.271300000000
31.0396030000000 121.193412000000
31.0652910000000 121.420516000000
31.1526520000000 121.314224000000
31.0687600000000 121.242162000000
31.0954570000000 121.351544000000
31.0930850000000 121.421098000000
31.0241010000000 121.208819000000
31.1561970000000 121.580258000000
31.0925010000000 121.520596000000
31.2174150000000 121.538298000000
31.1467460000000 121.497248000000
31.1613310000000 121.543094000000
31.1848830000000 121.480627000000
31.1178330000000 121.583561000000
31.3763000000000 121.471500000000
首先对于数据集进行可视化和载入操作
%加载数据
load('C:\Users\Administrator\Desktop\算法\tsp\tsp\city_location.mat');
%可视化数据
location = load('C:\Users\Administrator\Desktop\算法\tsp\tsp\city_location.mat');
x = location.city_location(:,1);
y = location.city_location(:,2);
plot(x,y,'ko');
xlabel('城市横坐标x');
ylabel('城市纵坐标y');
grid on; 

由于我们目标函数的计算的是路程的总和最短 我们需要将位置信息转换为距离
function D = Distance(a)
%计算两两城市之间的距离
%输入的数据为所有城市的x、y坐标位置矩阵a,输出为两两城市的距离构成的矩阵D
row = size(a,1);
D = zeros(row,row);
for i = 1:row
for j = i+1:row
D(i,j) = ((a(i,1) - a(j,1))^2 + (a(i,2)-a(j,2))^2)^0.5;
D(j,i) = D(i,j);
end根据上一节遗传算法的步骤
我们先进行遗传算法各项参数的初始化(后期根据数据情况可以调整参数)
NIND = 100; %种群大小
MAXGEN = 500; %最大迭代次数
Pc = 0.9; %交叉概率,相当于基因遗传的时候染色体交叉
Pm = 0.05; %染色体变异
GGAP = 0.9; %这个是代沟,通过遗传方式得到的子代数为父代数*GGAP在这之前我们需要自己设定参数种群的规模,一般情况下种群数目在20-160之间,如果种群数目较大会增加计算量延长收敛时间,如果太小不能提供足够的采样数据。
对于迭代次数,通常是在100-1000之间,取决于数据量的大小,需要看遗传算法是否对目标优化趋于平稳的状态,代数过多影响算法的速度,代数会使优化效果未达到最好就停止迭代,也可以采取达到某个条件停止迭代的方法。
对于交叉概率,一般取0.5-1.0,太高会使适应的结构很快就被破坏,太低搜索会始终停滞不前。
变异概率:通常取0.001-0.1,太小会使新的基因产生过少,太大会使遗传算法变为随机搜索。
代沟:就是上一代(假设总数为100)通过轮盘法筛选后要舍弃部分适应度低的基因(假设为20),则下一代就剩下80个基因.代购就是80/100=0.8,以此类推.
随机生成种群
function Chrom = InitPop(NIND,N)%初始化种群,
%输入:
%NIND:种群大小
%N:个体染色体长度(城市个数)
%输出:
%初始种群
Chrom = zeros(NIND,N); %用于存储种群
for i = 1:NIND
Chrom(i,:) = randperm(N);%随机生成初始种群,randperm函数:随机打乱一个数字序列,这里打乱从1-N的数字序列 也就是随机生成一种路线 一个新的个体
end下面编写一个函数将我们的路线图可视化 这样才能直观的看到旅行商的路线图
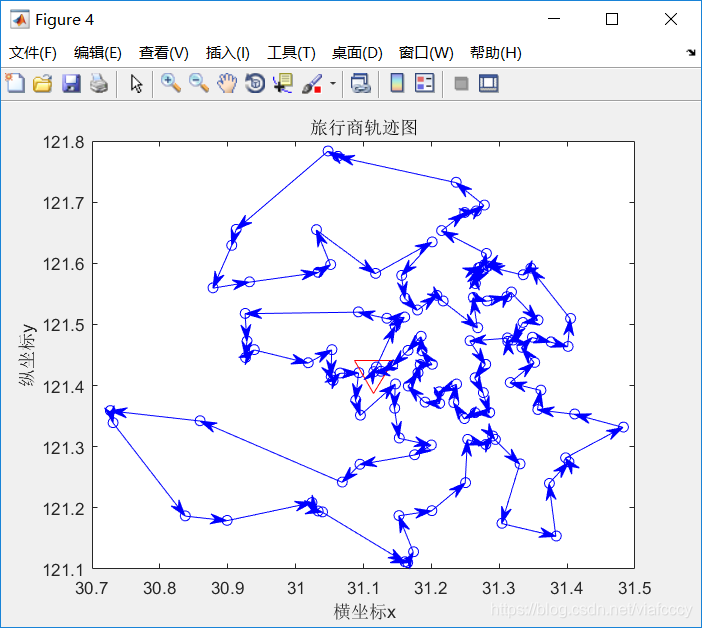
function DrawPath(Chrom,X)
%输入:
%待画路线
%城市的坐标位置
%输出:
%旅行商的路线
R = [Chrom(1,:) Chrom(1,1)]; %第一个随机解(个体)【Chrom(1,:)取第一行数据】,一共有n个城市,但是这里R有n+1个值,因为后面又补了一个Chrom(1,1),“是为了让路径最后再回到起点”
figure;
hold on
plot(X(:,1),X(:,2),'bo')%X(:,1),X(:,2)分别代表的X轴坐标和Y轴坐标
%plot(X(:,1),X(:,2),'o','color',[1,1,1])%X(:,1),X(:,2)分别代表的X轴坐标和Y轴坐标,
plot(X(Chrom(1,1),1),X(Chrom(1,1),2),'rv','MarkerSize',20)%标记起点
A = X(R,:); %A是将之前的坐标顺序用R打乱后重新存入A中
row = size(A,1); %row为坐标数+1
for i = 2:row
[arrowx,arrowy] = dsxy2figxy(gca,A(i-1:i,1),A(i-1:i,2)); %dsxy2figxy坐标转换函数,记录两个点
annotation('textarrow',arrowx,arrowy,'HeadWidth',8,'color',[0,0,1]);%将这两个点连接起来
end
hold off
xlabel('横坐标x')
ylabel('纵坐标y')
title('旅行商轨迹图')
box on 
同时由于数据的点可能很多 不能清晰的看到整个路线就需要 我们在命令行将路线打印出来
function p=OutputPath(R)
%打印路线函数
%以1->2->3的形式在命令行打印路线
R = [R,R(1)];
N = length(R);
p = num2str(R(1));
for i = 2:N
p = [p,'->',num2str(R(i))];
end
disp(p)接下来我们需要去确定我们的目标函数 也就是所有路线加起来的总和 旅行商走过的总路程 我们试图寻找它的最小值
function len = PathLength(D,Chrom)
%计算所有个体的路线长度
%输入
%D两两城市之间的距离
%Chrom个体的轨迹
[~,col] = size(D); %返回D的列数
NIND = size(Chrom,1);%NIND等于初始种群
len = zeros(NIND,1);%初始化一个大小等于NOND的len来记录长度
for i = 1:NIND
p = [Chrom(i,:) Chrom(i,1)];%构造p矩阵保存路线图 将第一行路线提出 再加上第一个构成回路
i1 = p(1:end-1);%i1从第一个开始遍历到倒数第二个
i2 = p(2:end);%i2从第二个开始遍历到倒数第一个
len(i,1) = sum(D((i1-1)*col+i2));%计算出每种路线(种群的个体)的长度
end以上完成了所有的准备工作 和 数据处理工作 下面开始使用遗传算法求解最优解
计算个体的适应度,适应度用于评价个体的优劣程度,适应度越大个体越好,反之适应度越小则个体越差;根据适应度的大小对个体进行选择,以保证适应性能好的个体有更多的机会繁殖后代,使优良特性得以遗传。因此,遗传算法要求适应度函数值必须是非负数,而在许多实际问题中,求解的目标通常是费用最小,而不是效益最大,因此需要将求最小的目标根据适应度函数非负原则转换为求最大目标的形式。
我们使用距离和的倒数作为适应度函数
function FitnV = Fintness(len) %适应度函数
%输入:
%len 个体的长度(TSP的距离)
%输出:
%FitnV 个体的适应度值
FitnV = 1./len;遗传算子
遗传算法包括三个遗传算子:选择(复制)、交叉(重组)、变异(突变)。算子的设计是遗传策略的主要组成部分,也是调控和控制进化的重要工具。
选择操作
确定父代如何选取个体遗传到下一代中
(1)轮盘赌法
又称比例选择方法.其基本思想是:各个个体被选中的概率与其适应度大小成正比.
本例使用的是轮盘赌法来完成选择的操作
具体操作如下:
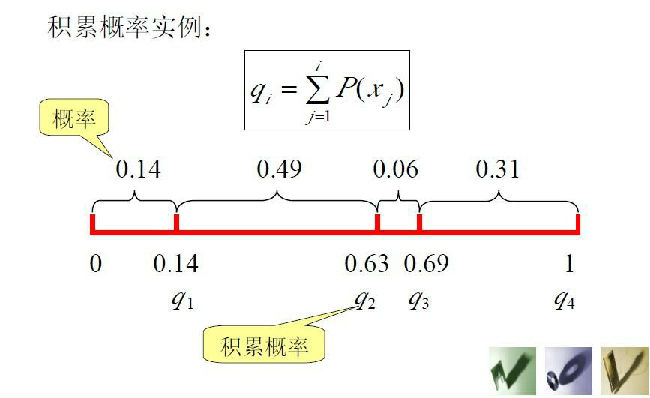
(1)计算出群体中每个个体的适应度f(i=1,2,…,M),M为群体大小;
(2)计算出每个个体被遗传到下一代群体中的概率;
(3)计算出每个个体的累积概率;
(q[i]称为染色体x[i] (i=1, 2, …, n)的积累概率)
(4)在[0,1]区间内产生一个均匀分布的伪随机数r;
(5)若r<q[1],则选择个体1,否则,选择个体k,使得:q[k-1]<r≤q[k] 成立;(6)重复(4)、(5)共M次
(2)排序算法
(3)两两竞争法
我们使用轮盘赌法来完成选择算子的实现
function NewChrIx = Sus(FitnV,Nsel)
%输入:
%FitnV 个体的是适应度值
%Nsel 被选个体的数目
%输出:
%NewChrIx 被选择个体的索引号
[Nind,ans] = size(FitnV);%Nind为FitnV的行数也就是个体数 ans为列数1
cumfit = cumsum(FitnV);%对适应度累加 例如 1 2 3 累加后 1 3 6 用来计算累积概率
trials = cumfit(Nind)/Nsel * (rand + (0:Nsel-1)');%cumfit(Nind)表示的是矩阵cumfit的第Nind个元素 A.'是一般转置,A'是共轭转置 rand返回一个在区间 (0,1) 内均匀分布的随机数
%cumfit(Nind)/Nsel平均适应度 * (rand +(0:Nsel-1)')从0开始到89的转置矩阵(行矩阵变列矩阵)加上每一项加上一个0-1的随机数
%生成随机数矩阵 用来筛选
Mf = cumfit(:,ones(1,Nsel));%将生成的累积概率 复制90份 生成一个100*90的矩阵
Mt = trials(:,ones(1,Nind))';
[NewChrIx,ans] = find(Mt<Mf & [zeros(1,Nsel);Mf(1:Nind-1,:)]<= Mt);%寻找满足条件的个体 返回返回数组 X 中每个元素的行和列下标
[ans,shuf] = sort(rand(Nsel,1));%生成Nsel*1的随机数矩阵 按升序对 A 的元素进行排序 返回选择的shuf 随机打乱个体顺序 保证后续遗传算子操作的随机性
NewChrIx = NewChrIx(shuf);%返回shuf索引的矩阵元素封装为select()选择个体
function SelCh = Select(Chrom,FitnV,GGAP)
%输入:
%Chrom 种群
%FitnV 适应度值
%GGAP 选择概率
%输出:
%SelCh 被选择的个体
NIND = size(Chrom,1);%种群个体总数
NSel = max(floor(NIND * GGAP+.5),2);%确定下一代种群的个体数,如果不足二个就计为二个
ChrIx = Sus(FitnV,NSel);
SelCh = Chrom(ChrIx,:);交叉

function [a,b] = intercross(a,b)
%输入:
%a和b为两个待交叉的个体
%输出:
%a和b为交叉后得到的两个个体
L = length(a);
%随机产生交叉区段
r1 = randsrc(1,1,[1:L]);%随机生成在1-L 的一个1*1的矩阵
r2 = randsrc(1,1,[1:L]);
if r1~=r2
a0 = a;
b0 = b;
s = min([r1,r2]);
e = max([r1,r2]);
for i = s:e
a1 = a;
b1 = b;
%第一次互换
a(i) = b0(i);
b(i) = a0(i);
%寻找相同的城市
x = find(a==a(i));
y = find(b==b(i));
%第二次互换产生新的解
i1 = x(x~=i);
i2 = y(y~=i);
if ~isempty(i1)
a(i1)=a1(i);
end
if ~isempty(i2)
b(i1)=b1(i);
end
end
end将交叉函数封装成为下面的函数
function SelCh = Recombin(SelCh,Pc)
%交叉操作
%输入:
%SelCh 被选择的个体
%Pc 交叉概率
%输出:
%SelCh 交叉后的个体
NSel = size(SelCh,1);
for i = 1:2:NSel - mod(NSel,2)
if Pc>=rand %交叉概率PC
[SelCh(i,:),SelCh(i+1,:)] = intercross(SelCh(i,:),SelCh(i+1,:));
end
end变异
function SelCh = Mutate(SelCh,Pm)
%变异操作
%输入:
%SelCh 被选择的个体
%Pm 变异概率
%输出:
%SelCh 变异后的个体
[NSel,L] = size(SelCh);
for i = 1:NSel
if Pm >= rand
R = randperm(L);
SelCh(i,R(1:2)) = SelCh(i,R(2:-1:1));
end
end
进化逆转:这个是标准的遗传算法没有的,是我们为了加速进化而加入的一个操作。这里的进化是指逆转操作具有单向性,即只有逆转之后个体变得更优才会执行逆转操作,否则逆转无效。具体的方法是,随机产生[1,10](这里仍然以10个城市为例)之间的两个随机数r1和r2(其实也是允许相同的,只是r1,r2相同之后,逆转自然无效,设置交叉变异都是无效的,但是这不会经常发生),然后将r1和r2之间的基因进行反向排序。比如对于染色体:
1 3 4 2 10 9 8 7 6 5
r1=3,r2=5,它们之间的基因反向排列之后得到的染色体如下:
1 3 10 2 4 9 8 7 6 5
function SelCh = Reverse(SelCh,D)
%进化逆转函数
%输入:
%SelCh 被选择的个体
%D 各城市的距离矩阵
%输出:
%SelCh 进化逆转后的个体
[row,col] = size(SelCh);
ObjV = PathLength(D,SelCh);
SelCh1 = SelCh;
for i = 1:row
r1 = randsrc(1,1,[1:col]);
r2 = randsrc(1,1,[1:col]);
mininverse = min([r1 r2]);
maxinverse = max([r1 r2]);
SelCh1(i,mininverse:maxinverse) = SelCh1(i,maxinverse:-1:mininverse);
end
ObjV1 = PathLength(D,SelCh1);%计算路线长度
index = ObjV1<ObjV;
SelCh(index,:)=SelCh1(index,:);更新种群
function Chrom = Reins(Chrom,SelCh,ObjV)
%重插入子代的种群
%输入:
%Chrom 父代的种群
%SelCh 子代的种群
%ObjV 父代适应度
%输出:
%Chrom 组合父代与子代后得到的新种群
NIND = size(Chrom,1);
NSel = size(SelCh,1);
[TobjV,index] = sort(ObjV);
Chrom = [Chrom(index(1:NIND-NSel),:);SelCh];这样就完成了主体代码 看全部的代码可以到github上下载https://github.com/viafcccy/TSP
结果:
3000代下的情况,

最优解:
78->35->118->50->52->116->60->68->63->59->104->47->106->105->109->113->48->112->84->82->110->2->54->107->111->67->61->62->65->64->114->46->108->5->7->4->6->1->55->34->77->75->30->33->32->76->74->73->31->24->25->71->27->28->20->29->70->122->21->22->94->90->95->91->89->40->96->92->88->93->42->39->102->38->103->100->97->101->41->66->44->43->45->98->121->99->115->119->51->49->117->56->10->15->8->17->26->72->23->19->69->9->12->11->58->57->18->3->13->14->16->53->83->37->79->86->81->85->120->36->80->87->78
旅行商走过的总距离:5.7184










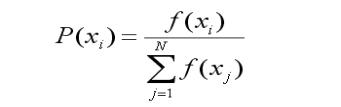














 1346
1346











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








