图像分割是模式识别和计算机视觉中很重要的一个部分,基于阈值的图像分割具有简单、计算量小、效率高等特点,在实际图像处理中具有广泛的应用。经过国内外学者的广泛努力,已经提出了数以百计的阈值分割的算法,依据阈值分割算法本身所具有的准则或特性,可以分为迭代法、最大类间误差法(Otsu)、最大熵法等。本文主要介绍以上几种阈值分割方法。
(一)迭代法
迭代法是一种比较简单的阈值分割方法,其思想:设置阈值的初始值为图像灰度最大值和最小值的平均,根据阈值划分图像为目标和背景,并分别将其灰度值求和,计算目标和背景的平均灰度,并判断阈值是否等于目标和背景平均灰度的和的平均,若相等,则阈值即为其平均,否则,将阈值设置为目标和背景灰度平局值的和的一半,继续迭代,直至计算出阈值。
算法过程:
1、计算图像的最大灰度值Zmax、最小灰度值Zmin,求平均得到初始阈值tk。
zmax=max(max(I));zmin=min(min(I));
tk=(zmax+zmin)/2;
2、根据阈值划分图像为目标和背景,并分别计算其灰度均值
z1=foregroundsum/iforeground;
z2=foregroundsum/ibackground;
tktmp=uint8((z1+z2)/2);
3、判断tk是否等于tktmp,若相等则退出循环,阈值为tktmp,否则,将tktmp赋给tk,转2继续执行迭代。
参考代码:
close all;%关闭所有窗口
clear;%清除变量的状态数据
clc;%清除命令行
I=imread('rice.png');
subplot(1,2,1);
imshow(I);
title('1 rice的原图');
%迭代式阈值分割
zmax=max(max(I));%取出最大灰度值
zmin=min(min(I));%取出最小灰度值
tk=(zmax+zmin)/2;
bcal=1;
[m,n]=size(I);
while(bcal)
%定义前景和背景数
iforeground=0;
ibackground=0;
%定义前景和背景灰度总和
foregroundsum=0;
backgroundsum=0;
for i=1:m
for j=1:n
tmp=I(i,j);
if(tmp>=tk)
%前景灰度值
iforeground=iforeground+1;
foregroundsum=foregroundsum+double(tmp);
else
ibackground=ibackground+1;
backgroundsum=backgroundsum+double(tmp);
end
end
end
%计算前景和背景的平均值
z1=foregroundsum/iforeground;
z2=foregroundsum/ibackground;
tktmp=uint8((z1+z2)/2);
if(tktmp==tk)
bcal=0;
else
tk=tktmp;
end
%当阈值不再变化时,说明迭代结束
end
disp(strcat('迭代的阈值:',num2str(tk)));%在command window里显示出 :迭代的阈值:阈值
newI=im2bw(I,double(tk)/255);%函数im2bw使用阈值(threshold)变换法把灰度图像(grayscale image) (二)最大类间误差法(Otus)
大津算法是1979年日本学者大津在文章A Tlreshold Selection Method from Gray-Level Histograms中提出的自适应的阈值确定的方法,简称OTSU。其思想:根据灰度特性,将图像分为目标和背景2部分,目标和背景之间的类间差越大,说明构成图像的2部分的差别越大,因此类间方差最大的分割即意味着错分概率最小,计算以每个灰度值为阈值的分割的类间方差,其中类间方差最大的值即为阈值。
算法过程:
1、计算每个灰度值的概率并计算目标和背景的分布概率以及平均灰度值和方差。
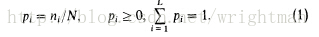
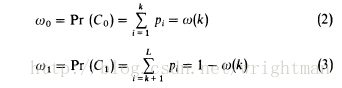
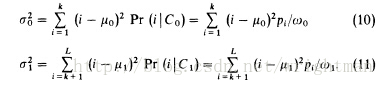
2、计算类间差
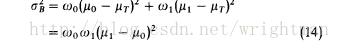
3、取类间差最大的灰度值即为阈值
参考代码:
Matlab实现了大津算法。
close all;%关闭所有窗口
[plain] view plain copy
clear;%清除变量的状态数据
clc;%清除命令行
I=imread('rice.png');
subplot(1,2,1);
imshow(I);
title('1 rice的原图');
bw=graythresh(I);
disp(strcat('otsu阈值分割的阈值:',num2str(bw*255)));%在command window里显示出 :迭代的阈值:阈值
newII=im2bw(I,bw);
subplot(1,2,2);
imshow(newII);
title('2 rice的otsu阈值分割'); (三)、最小误差法
最小误差法是KITTLER1984年在MINIMUM ERROR THRESHOLDING文章中提出的一种基于直方图的阈值分割方法,简称KITTLER算法。其思想:假设灰度图像由目标和背景组成,且目标和背景满足一混合高斯分布,计算目标和背景的均值、方差,根据最小分类误差思想得到的最小误差目标函数,取目标函数最小时的阈值即为最佳阈值。按此阈值将图像分割为二值图像。
算法过程:
1、计算目标和背景的均值、方差。
2、根据最小分类误差思想得到最小误差目标函数。
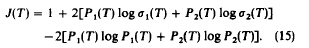
3、取使目标函数最小值为阈值。
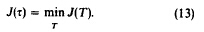
参考代码:
[plain] view plain copy
I = imread(‘rice.bmp’);
MAXD = 100000;
imag = imag(:,:,1);
[counts, x] = imhist(imag); % counts are the histogram. x is the intensity level.
GradeI = length(x); % the resolusion of the intensity. i.e. 256 for uint8.
J_t = zeros(GradeI, 1); % criterion function
prob = counts ./ sum(counts); % Probability distribution
meanT = x’ * prob; % Total mean level of the picture
% Initialization
w0 = prob(1); % Probability of the first class
miuK = 0; % First-order cumulative moments of the histogram up to the kth level.
J_t(1) = MAXD;
n = GradeI-1;
for i = 1 : n
w0 = w0 + prob(i+1);
miuK = miuK + i * prob(i+1); % first-order cumulative moment
if (w0 == 0) || (w0 == 1)
J_t(i+1) = MAXD; % T = i
else
miu1 = miuK / w0;
miu2 = (meanT-miuK) / (1-w0);
var1 = (((0 : i)’-miu1).^2)’ * prob(1 : i+1);
var1 = var1 / w0; % variance
var2 = (((i+1 : n)’-miu2).^2)’ * prob(i+2 : n+1);
var2 = var2 / (1-w0);
if var1 > 0 && var2 > 0 % in case of var1=0 or var2 =0
J_t(i+1) = 1+2*w0 * log(var1)+2*(1-w0) * log(var2)-2*w0*log(w0)-2*(1-w0)*log(1-w0);
else
J_t(i+1) = MAXD;
end
end
end
minJ = min(J_t);
index = find(J_t == minJ);
th = mean(index);
th = (th-1)/n
imagBW = im2bw(imag, th);
figure, imshow(I_bw);








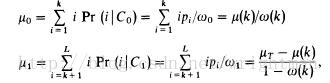
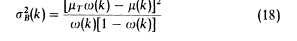
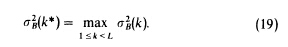
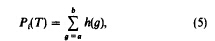
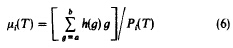
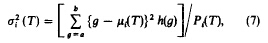
















 2231
2231

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








